การถดถอยเชิงเส้นพหุคูณคืออะไร และควรใช้เมื่อไหร่ในวิทยานิพนธ์?

การถดถอยเชิงเส้นพหุคูณ (multiple linear regression) เป็นการทำนายค่าของตัวแปรตาม (Y) จากตัวแปรอิสระตั้งแต่สองตัวขึ้นไป (X₁, X₂, X₃...) ใช้เมื่อต้องการเข้าใจว่าหลายปัจจัยร่วมกันทำนายผลลัพธ์อย่างไร เช่น 'ชั่วโมงการเรียน การนอน และการเข้าเรียน ร่วมกันทำนายคะแนนสอบหรือไม่?' สำหรับงานวิจัย การถดถอยพหุคูณเหมาะเมื่อมีตัวแปรทำนายต่อเนื่องหลายตัว ต้องการควบคุมตัวแปรกวน หรือต้องการเปรียบเทียบความสำคัญสัมพัทธ์ของตัวแปรทำนายแต่ละตัว

การถดถอยเชิงเส้นอย่างง่ายกับการถดถอยเชิงเส้นพหุคูณต่างกันอย่างไร?

การถดถอยเชิงเส้นอย่างง่าย (simple linear regression) ใช้ตัวแปรทำนายหนึ่งตัว (Y = a + bX) ในขณะที่การถดถอยเชิงเส้นพหุคูณใช้ตัวแปรทำนายสองตัวขึ้นไป (Y = a + b₁X₁ + b₂X₂ + ...) การถดถอยอย่างง่ายตอบคำถาม 'X ทำนาย Y หรือไม่?' ในขณะที่การถดถอยพหุคูณตอบคำถาม 'X₁, X₂ และ X₃ ร่วมกันทำนาย Y หรือไม่ และตัวทำนายใดสำคัญที่สุด?' การถดถอยพหุคูณยังช่วยให้ควบคุมตัวแปรกวนและเห็นการมีส่วนร่วมเฉพาะของตัวแปรทำนายแต่ละตัวขณะที่ตัวอื่นคงที่

R² ปรับแก้คืออะไร และสำคัญอย่างไรในการถดถอยพหุคูณ?

R² ปรับแก้ (Adjusted R²) ปรับแก้สำหรับจำนวนตัวแปรทำนายในโมเดล ค่า R² ปกติจะเพิ่มขึ้นเสมอเมื่อเพิ่มตัวแปรทำนาย แม้ตัวแปรนั้นจะไม่มีประโยชน์ก็ตาม R² ปรับแก้จะลงโทษการเพิ่มตัวแปรที่ไม่ช่วยอะไร และสามารถลดลงได้หากตัวแปรใหม่ไม่ช่วยเพิ่มการทำนายเพียงพอ ใช้ R² ปรับแก้ (ไม่ใช่ R² ปกติ) เมื่อเปรียบเทียบโมเดลที่มีจำนวนตัวแปรทำนายต่างกัน หรือประเมินว่าการเพิ่มตัวแปรคุ้มค่าหรือไม่ ในวิทยานิพนธ์ ควรรายงานทั้ง R² และ R² ปรับแก้เพื่อความโปร่งใส

จะรู้ได้อย่างไรว่าตัวแปรทำนายใดมีนัยสำคัญทางสถิติในการถดถอยพหุคูณ?

ดูค่า p-value ของตัวแปรทำนายแต่ละตัวในตาราง Coefficients ถ้า p < 0.05 ตัวแปรทำนายนั้นมีนัยสำคัญทางสถิติ หมายความว่ามีส่วนร่วมเฉพาะในการทำนาย Y หลังจากควบคุมตัวแปรทำนายอื่นแล้ว ตัวแปรทำนายที่ไม่มีนัยสำคัญ (p ≥ 0.05) ไม่เพิ่มคุณค่าในการทำนายนอกเหนือจากตัวแปรอื่น สิ่งสำคัญคือ ตัวแปรทำนายสามารถมีนัยสำคัญในการถดถอยอย่างง่าย แต่ไม่มีนัยสำคัญในการถดถอยพหุคูณ หากมันทับซ้อนกับตัวแปรทำนายอื่น (multicollinearity)

ข้อตกลงเบื้องต้นอะไรบ้างที่ต้องตรวจสอบสำหรับการถดถอยเชิงเส้นพหุคูณ?

การถดถอยพหุคูณมีข้อตกลงเบื้องต้นหลัก 5 ข้อ: (1) ความเป็นเส้นตรง - ความสัมพันธ์ระหว่าง X แต่ละตัวกับ Y เป็นเส้นตรง; (2) ความเป็นอิสระ - ข้อมูลแต่ละชุดเป็นอิสระต่อกัน; (3) การแจกแจงปกติของค่าคงเหลือ - ความคลาดเคลื่อนมีการแจกแจงปกติ; (4) ความแปรปรวนคงที่ (Homoscedasticity) - ค่าคงเหลือมีความแปรปรวนคงที่; (5) ไม่มี multicollinearity - ตัวแปรทำนายไม่มีความสัมพันธ์สูงระหว่างกัน ข้อตกลงที่ 5 เป็นข้อที่เฉพาะสำหรับการถดถอยพหุคูณ การละเมิดข้อตกลงเบื้องต้นอาจทำให้ค่าสัมประสิทธิ์เบี่ยงเบนและ p-values ไม่ถูกต้อง

จะรายงานผลการถดถอยพหุคูณในรูปแบบ APA 7 ได้อย่างไร?

รายงาน: (1) ข้อความวิเคราะห์: 'ดำเนินการวิเคราะห์การถดถอยเชิงเส้นพหุคูณเพื่อทำนาย...' (2) ความเหมาะสมของโมเดล: 'โมเดลมีนัยสำคัญทางสถิติ, F(3, 26) = 373.65, p < .001, R² = .98, adjusted R² = .97' (3) ตัวแปรทำนายแต่ละตัว: 'ชั่วโมงการเรียนทำนายคะแนนสอบอย่างมีนัยสำคัญ (B = 1.75, p < .001) เช่นเดียวกับการเข้าชั้นเรียน (B = 2.36, p < .001) ชั่วโมงการนอนไม่ใช่ตัวทำนายที่มีนัยสำคัญ (B = 0.52, p = .092)' รวมตาราง regression ที่มี B, SE, β, t, p และ 95% CI สำหรับตัวแปรทำนายแต่ละตัว

ต้องมีข้อมูลกี่ตัวอย่างสำหรับการถดถอยพหุคูณ?

ขนาดตัวอย่างขั้นต่ำขึ้นอยู่กับจำนวนตัวแปรทำนาย สูตรทั่วไปคือ n ≥ 50 + 8k (เมื่อ k = จำนวนตัวแปรทำนาย) สำหรับทดสอบตัวแปรทำนายแต่ละตัว หรือ n ≥ 104 + k สำหรับทดสอบโมเดลโดยรวม สำหรับตัวแปรทำนาย 3 ตัว: ขั้นต่ำ n = 74 สำหรับตัวทำนาย, n = 107 สำหรับโมเดล อย่างไรก็ตาม n = 100-200 แนะนำสำหรับค่าประมาณที่เสถียรในงานวิจัย แนวปฏิบัติที่ดีคือ ทำการวิเคราะห์ power analysis โดยใช้ G*Power ก่อนเก็บข้อมูลเพื่อกำหนดขนาดตัวอย่างที่แน่นอน

วิธีทำการถดถอยเชิงเส้นพหุคูณใน Excel (คู่มือสำหรับวิทยานิพนธ์)

Q: ข้อตกลงเบื้องต้นอะไรบ้างที่ต้องตรวจสอบสำหรับการถดถอยเชิงเส้นพหุคูณ?

การถดถอยพหุคูณมีข้อตกลงเบื้องต้นหลัก 5 ข้อ: (1) ความเป็นเส้นตรง - ความสัมพันธ์ระหว่าง X แต่ละตัวกับ Y เป็นเส้นตรง; (2) ความเป็นอิสระ - ข้อมูลแต่ละชุดเป็นอิสระต่อกัน; (3) การแจกแจงปกติของค่าคงเหลือ - ความคลาดเคลื่อนมีการแจกแจงปกติ; (4) ความแปรปรวนคงที่ (Homoscedasticity) - ค่าคงเหลือมีความแปรปรวนคงที่; (5) ไม่มี multicollinearity - ตัวแปรทำนายไม่มีความสัมพันธ์สูงระหว่างกัน ข้อตกลงที่ 5 เป็นข้อที่เฉพาะสำหรับการถดถอยพหุคูณ การละเมิดข้อตกลงเบื้องต้นอาจทำให้ค่าสัมประสิทธิ์เบี่ยงเบนและ p-values ไม่ถูกต้อง

Q: จะรายงานผลการถดถอยพหุคูณในรูปแบบ APA 7 ได้อย่างไร?

รายงาน: (1) ข้อความวิเคราะห์: 'ดำเนินการวิเคราะห์การถดถอยเชิงเส้นพหุคูณเพื่อทำนาย...' (2) ความเหมาะสมของโมเดล: 'โมเดลมีนัยสำคัญทางสถิติ, F(3, 26) = 373.65, p < .001, R² = .98, adjusted R² = .97' (3) ตัวแปรทำนายแต่ละตัว: 'ชั่วโมงการเรียนทำนายคะแนนสอบอย่างมีนัยสำคัญ (B = 1.75, p < .001) เช่นเดียวกับการเข้าชั้นเรียน (B = 2.36, p < .001) ชั่วโมงการนอนไม่ใช่ตัวทำนายที่มีนัยสำคัญ (B = 0.52, p = .092)' รวมตาราง regression ที่มี B, SE, β, t, p และ 95% CI สำหรับตัวแปรทำนายแต่ละตัว

Q: ต้องมีข้อมูลกี่ตัวอย่างสำหรับการถดถอยพหุคูณ?

ขนาดตัวอย่างขั้นต่ำขึ้นอยู่กับจำนวนตัวแปรทำนาย สูตรทั่วไปคือ n ≥ 50 + 8k (เมื่อ k = จำนวนตัวแปรทำนาย) สำหรับทดสอบตัวแปรทำนายแต่ละตัว หรือ n ≥ 104 + k สำหรับทดสอบโมเดลโดยรวม สำหรับตัวแปรทำนาย 3 ตัว: ขั้นต่ำ n = 74 สำหรับตัวทำนาย, n = 107 สำหรับโมเดล อย่างไรก็ตาม n = 100-200 แนะนำสำหรับค่าประมาณที่เสถียรในงานวิจัย แนวปฏิบัติที่ดีคือ ทำการวิเคราะห์ power analysis โดยใช้ G*Power ก่อนเก็บข้อมูลเพื่อกำหนดขนาดตัวอย่างที่แน่นอน

การถดถอยเชิงเส้นพหุคูณ (multiple linear regression) ขยายการถดถอยอย่างง่ายโดยให้คุณทำนายผลลัพธ์โดยใช้ตัวแปรทำนายสองตัวขึ้นไปพร้อมกัน สิ่งนี้จำเป็นสำหรับการวิจัยวิทยานิพนธ์ที่ปรากฏการณ์ในโลกจริงไม่ค่อยอธิบายได้ด้วยปัจจัยเดียว ไม่ว่าจะเป็นการทำนายผลการเรียนจากพฤติกรรมการเรียน การนอน และการเข้าเรียน หรือการพยากรณ์ยอดขายจากการโฆษณา การตั้งราคา และฤดูกาล การถดถอยพหุคูณเผยให้เห็นว่าตัวแปรทำนายใดสำคัญที่สุดและทำงานร่วมกันอย่างไร

ต่างจากการถดถอยอย่างง่ายที่ตอบคำถาม "X ทำนาย Y หรือไม่?" การถดถอยพหุคูณตอบคำถามที่สมจริงกว่า: "X₁, X₂ และ X₃ ร่วมกันทำนาย Y หรือไม่ และตัวแปรทำนายใดมีผลมากที่สุด?" ทำให้มันเป็นหนึ่งในเทคนิคทางสถิติที่ใช้กันมากที่สุดในงานวิจัยวิทยานิพนธ์ ครอบคลุมสาขาจิตวิทยา การศึกษา ธุรกิจ วิทยาศาสตร์สุขภาพ และสังคมศาสตร์

คู่มือที่ครอบคลุมนี้จะแสดงวิธีทำการถดถอยเชิงเส้นพหุคูณใน Excel โดยใช้ Analysis ToolPak แปลผลอย่างถูกต้อง (รวมถึง R² ปรับแก้และนัยสำคัญของตัวแปรทำนายแต่ละตัว) ตรวจจับปัญหา multicollinearity ตรวจสอบข้อตกลงเบื้องต้น และรายงานผลในรูปแบบ APA 7 คุณจะได้เรียนรู้ข้อจำกัดสำคัญของ Excel และเมื่อใดที่ต้องใช้ SPSS หรือ R แทน

ประเด็นสำคัญ:

การถดถอยพหุคูณทำนาย Y จากตัวแปรทำนายตั้งแต่ 2 ตัวขึ้นไปพร้อมกัน
รายงาน R² ปรับแก้ (ไม่ใช่ R² ปกติ) เสมอ เพราะมันปรับแก้สำหรับจำนวนตัวแปรทำนาย
ตรวจสอบ multicollinearity ก่อน โดยใช้ correlation matrix (ตัวแปรทำนายควรมี r < 0.80)
โมเดลโดยรวมที่มีนัยสำคัญ (F-test) ไม่ได้หมายความว่าตัวแปรทำนายทุกตัวมีนัยสำคัญ
Excel จัดการการถดถอยพหุคูณมาตรฐานได้ดี แต่ไม่สามารถทำ stepwise, hierarchical หรือ logistic regression

ก่อนเริ่มต้น: คู่มือนี้ถือว่าคุณเข้าใจการถดถอยเชิงเส้นอย่างง่ายแล้ว - อ่านบทความนั้นก่อนถ้าคุณเพิ่งเริ่มเรียนเรื่อง regression นอกจากนี้คุณต้องมี Excel ที่ติดตั้ง Analysis ToolPak แล้ว หากยังไม่ได้เปิดใช้งาน ดูคู่มือของเราวิธีเปิดใช้งาน Data Analysis ใน Excel

การถดถอยเชิงเส้นพหุคูณคืออะไร?

การถดถอยเชิงเส้นพหุคูณ (multiple linear regression) เป็นวิธีทางสถิติที่สร้างโมเดลความสัมพันธ์ระหว่างตัวแปรอิสระสองตัวขึ้นไป (ตัวแปรทำนาย, X₁, X₂, X₃...) และตัวแปรตามหนึ่งตัว (ผลลัพธ์, Y) โดยการปรับสมการเชิงเส้นให้เข้ากับข้อมูลที่สังเกตได้ มันขยายการถดถอยอย่างง่ายเพื่อรองรับหลายปัจจัยที่อาจมีผลต่อผลลัพธ์ของคุณ

สมการการถดถอยพหุคูณ

ถ้าคุณอ่านตำราสถิติหรือดูวิดีโอสอน คุณอาจสังเกตว่าสูตร regression เขียนต่างกันขึ้นอยู่กับแหล่งข้อมูล ไม่ต้องกังวล - ทั้งสองแบบถูกต้อง ความแตกต่างเป็นเพียงข้อตกลงในการเขียนสัญลักษณ์ และการเข้าใจทั้งสองแบบจะช่วยให้คุณอ่านแหล่งข้อมูลสถิติใดๆ ได้อย่างมั่นใจ

ในตำราสถิติเชิงทฤษฎี โดยทั่วไปจะใช้อักษรกรีก (สัญลักษณ์เบต้า) การเขียนแบบนี้แทนพารามิเตอร์ประชากรที่แท้จริง - ค่า "จริง" ที่มีอยู่ในประชากรทั้งหมดที่เราพยายามประมาณ:

$Y = \beta_0 + \beta_1X_1 + \beta_2X_2 + \beta_3X_3 + ... + \varepsilon$

ในคู่มือประยุกต์และบทเรียน Excel (รวมถึงบทความนี้) มักจะใช้อักษรโรมัน (a และ b) การเขียนแบบนี้แทนค่าประมาณจากตัวอย่าง - ค่าจริงที่ Excel คำนวณจากข้อมูลของคุณเพื่อประมาณพารามิเตอร์ประชากรเหล่านั้น:

$Y = a + b_1X_1 + b_2X_2 + b_3X_3 + ... + \varepsilon$

สรุป: เมื่อเห็น β₀ ในตำรา และ "Intercept" ใน Excel สิ่งเหล่านั้นหมายถึงสิ่งเดียวกัน เมื่ออาจารย์เขียน β₁ บนกระดานและ Excel แสดงค่าสัมประสิทธิ์ 2.15 นั่นคือแนวคิดเดียวกัน Excel ติดป้ายผลลัพธ์เป็น "Coefficients" โดยไม่คำนึงว่าตำราของคุณใช้สัญลักษณ์แบบใด

โดยที่:

Y = ตัวแปรตาม (สิ่งที่คุณทำนาย)
X₁, X₂, X₃ = ตัวแปรอิสระ (ตัวแปรทำนาย)
β₀ หรือ a = จุดตัดแกน (ค่า Y ที่คาดหวังเมื่อตัวแปร X ทั้งหมด = 0)
β₁, β₂, β₃ หรือ b₁, b₂, b₃ = ค่าสัมประสิทธิ์ความชัน (การเปลี่ยนแปลงของ Y สำหรับแต่ละหน่วยที่เพิ่มขึ้นของ X นั้น โดยคงตัวแปรทำนายอื่นไว้คงที่)
ε = ค่าความคลาดเคลื่อน (ความแปรผันที่อธิบายไม่ได้)

ตัวอย่างเช่น ถ้าคุณทำนายคะแนนสอบจากชั่วโมงการเรียน การนอน และการเข้าเรียน:

$\text{คะแนนสอบ (Exam Score)} = 33.14 + 1.75(\text{ชั่วโมงการเรียน}) + 0.52(\text{การนอน}) + 2.36(\text{การเข้าเรียน})$

นี่หมายความว่า: ทุกชั่วโมงการเรียนที่เพิ่มขึ้นจะเพิ่มคะแนนสอบ 1.75 คะแนน (โดยคงการนอนและการเข้าเรียนไว้คงที่) ทุกชั่วโมงการนอนที่เพิ่มขึ้นเพิ่ม 0.52 คะแนน และทุกคาบเรียนที่เข้าเพิ่มขึ้นเพิ่ม 2.36 คะแนน

ข้อได้เปรียบสำคัญ: "เมื่อคงตัวแปรอื่นไว้คงที่"

วลี "เมื่อคงตัวแปรอื่นไว้คงที่" (เรียกอีกอย่างว่า "ควบคุมไว้") คือสิ่งที่ทำให้การถดถอยพหุคูณมีพลัง ในการถดถอยอย่างง่าย ถ้าชั่วโมงการเรียนทำนายคะแนนสอบ คุณไม่สามารถบอกได้ว่ามันเป็นผลจากชั่วโมงการเรียนจริงๆ หรือสิ่งที่สัมพันธ์กับมัน (เช่น การเข้าเรียน) การถดถอยพหุคูณแยกผลเหล่านี้ออก:

การถดถอยอย่างง่าย: "นักศึกษาที่เรียนมากกว่าได้คะแนนสูงกว่า" (แต่อาจเป็นเพราะพวกเขาเข้าเรียนมากกว่าด้วย)
การถดถอยพหุคูณ: "นักศึกษาที่เรียนมากกว่าได้คะแนนสูงกว่า แม้เมื่อเราคำนึงถึงการเข้าเรียนของพวกเขา"

สิ่งนี้ช่วยให้คุณแยกส่วนร่วมเฉพาะของตัวแปรทำนายแต่ละตัว - จำเป็นสำหรับการสร้างข้อโต้แย้งเชิงสาเหตุในบทอภิปรายของวิทยานิพนธ์

เมื่อใดควรใช้การถดถอยเชิงเส้นพหุคูณสำหรับวิทยานิพนธ์

ใช้การถดถอยเชิงเส้นพหุคูณเมื่องานวิจัยของคุณตรงตามเกณฑ์เหล่านี้:

1. ข้อกำหนดคำถามวิจัย:

คุณต้องการทำนาย Y โดยใช้หลายปัจจัยพร้อมกัน
คุณต้องการควบคุมตัวแปรกวน
คุณต้องการกำหนดว่าตัวแปรทำนายใดสำคัญที่สุด
คุณต้องการเปรียบเทียบความสำคัญสัมพัทธ์ของตัวแปรทำนายต่างๆ

2. ข้อกำหนดตัวแปร:

ตัวแปรทำนายต่อเนื่องสองตัวขึ้นไป (X₁, X₂ ฯลฯ): มาตราวัดแบบช่วงหรืออัตราส่วน
ตัวแปรตามต่อเนื่องหนึ่งตัว (Y): มาตราวัดแบบช่วงหรืออัตราส่วน
ขนาดตัวอย่างขั้นต่ำ: n ≥ 50 + 8k (เมื่อ k = จำนวนตัวแปรทำนาย)

3. ตัวอย่างงานวิจัยตามสาขาวิชา:

จิตวิทยา: ชั่วโมงบำบัด การใช้ยาตามแพทย์สั่ง และการสนับสนุนทางสังคม ร่วมกันทำนายการลดอาการซึมเศร้าหรือไม่?
การศึกษา: ชั่วโมงการเรียน คุณภาพการนอน และการเข้าเรียน ร่วมกันทำนายคะแนนสอบหรือไม่?
ธุรกิจ: งบประมาณโฆษณา ราคา และกิจกรรมคู่แข่ง ร่วมกันทำนายรายได้จากการขายหรือไม่?
วิทยาศาสตร์สุขภาพ: การออกกำลังกาย คุณภาพอาหาร และการใช้ยาตามแพทย์สั่ง ร่วมกันทำนายการลดน้ำหนักหรือไม่?
สังคมศาสตร์: รายได้ การศึกษา และเครือข่ายสังคม ร่วมกันทำนายความพึงพอใจในชีวิตหรือไม่?

การถดถอยอย่างง่าย vs การถดถอยพหุคูณ: คุณต้องการแบบไหน?

ก่อนดำเนินการต่อ ตรวจสอบให้แน่ใจว่าการถดถอยพหุคูณเป็นตัวเลือกที่ถูกต้องสำหรับคำถามวิจัยของคุณ:

แผนภูมิการตัดสินใจสำหรับเลือกระหว่างการถดถอยเชิงเส้นอย่างง่าย (ตัวแปรทำนายหนึ่งตัว) และการถดถอยเชิงเส้นพหุคูณ (ตัวแปรทำนายสองตัวขึ้นไป) ตามคำถามวิจัยและการควบคุมตัวแปรกวน

รูปที่ 1: แผนภูมิการตัดสินใจสำหรับเลือกการถดถอยเชิงเส้นอย่างง่าย (ตัวแปรทำนายหนึ่งตัว) หรือการถดถอยเชิงเส้นพหุคูณ (ตัวแปรทำนายสองตัวขึ้นไป) ตามคำถามวิจัย

คุณสมบัติ	การถดถอยเชิงเส้นอย่างง่าย	การถดถอยเชิงเส้นพหุคูณ
จำนวนตัวแปรทำนาย	ตัวแปรอิสระ 1 ตัว	ตัวแปรอิสระ 2 ตัวขึ้นไป
สมการ	Y = a + bX	Y = a + b₁X₁ + b₂X₂ + b₃X₃...
คำถามวิจัย	"ชั่วโมงการเรียน (Study_Hours) ทำนายคะแนนสอบหรือไม่?"	"ชั่วโมงการเรียน (Study_Hours), การนอน (Sleep_Hours) และการเข้าเรียน (Classes_Attended) ร่วมกันทำนายคะแนนสอบหรือไม่?"
ควบคุมตัวแปรกวน	ไม่	ใช่ - แยกผลเฉพาะ
เปรียบเทียบความสำคัญของตัวแปรทำนาย	ไม่เกี่ยวข้อง (มีตัวแปรทำนายเดียว)	ใช่ - ตัวแปรทำนายใดสำคัญที่สุด?
สถิติสำคัญ	R²	R² ปรับแก้ (ปรับแก้สำหรับจำนวนตัวแปรทำนาย)
ข้อตกลงเบื้องต้นเพิ่มเติม	ไม่มี	ไม่มี multicollinearity ระหว่างตัวแปรทำนาย
ความสามารถของ Excel	รองรับเต็มรูปแบบ	รองรับเต็มรูปแบบ (แต่ไม่มีการคำนวณ VIF)

ตารางที่ 1: การเปรียบเทียบการถดถอยเชิงเส้นอย่างง่ายกับการถดถอยเชิงเส้นพหุคูณ

ใช้การถดถอยเชิงเส้นอย่างง่ายเมื่อ:

คุณมีตัวแปรทำนายเพียงหนึ่งตัว
คำถามวิจัยของคุณมุ่งเน้นที่ความสัมพันธ์เฉพาะหนึ่งอย่าง
คุณกำลังทำการวิเคราะห์เบื้องต้นก่อนเพิ่มตัวแปรทำนายอื่น
ตัวอย่าง: "งบประมาณโฆษณาทำนายยอดขายหรือไม่?"

ใช้การถดถอยเชิงเส้นพหุคูณเมื่อ:

คุณมีตัวแปรทำนายสองตัวขึ้นไป
คุณต้องการควบคุมตัวแปรกวน
คุณต้องการเปรียบเทียบความสำคัญสัมพัทธ์ของตัวแปรทำนาย
คุณกำลังทดสอบโมเดลทฤษฎีที่มีหลายปัจจัย
ตัวอย่าง: "งบประมาณโฆษณา ราคา และฤดูกาล ร่วมกันทำนายยอดขายหรือไม่ และปัจจัยใดสำคัญที่สุด?"

คำถามวิจัยแตกต่างกัน? หากคุณต้องการเปรียบเทียบค่าเฉลี่ยของกลุ่มแทนที่จะทำนายผลลัพธ์ต่อเนื่อง ดูคู่มือของเราเลือก T-Test หรือ ANOVA

ชุดข้อมูลตัวอย่างสำหรับบทเรียนนี้

ตลอดคู่มือนี้ เราจะใช้ชุดข้อมูลวิทยานิพนธ์ที่สมจริง ศึกษาว่าหลายปัจจัยทำนายผลการสอบของนักศึกษามหาวิทยาลัย 30 คนอย่างไร สิ่งนี้แสดงคำถามวิจัยทั่วไป: "ชั่วโมงการเรียน (Study_Hours) คุณภาพการนอน (Sleep_Hours) และการเข้าเรียน (Classes_Attended) ร่วมกันทำนายผลการเรียนหรือไม่?"

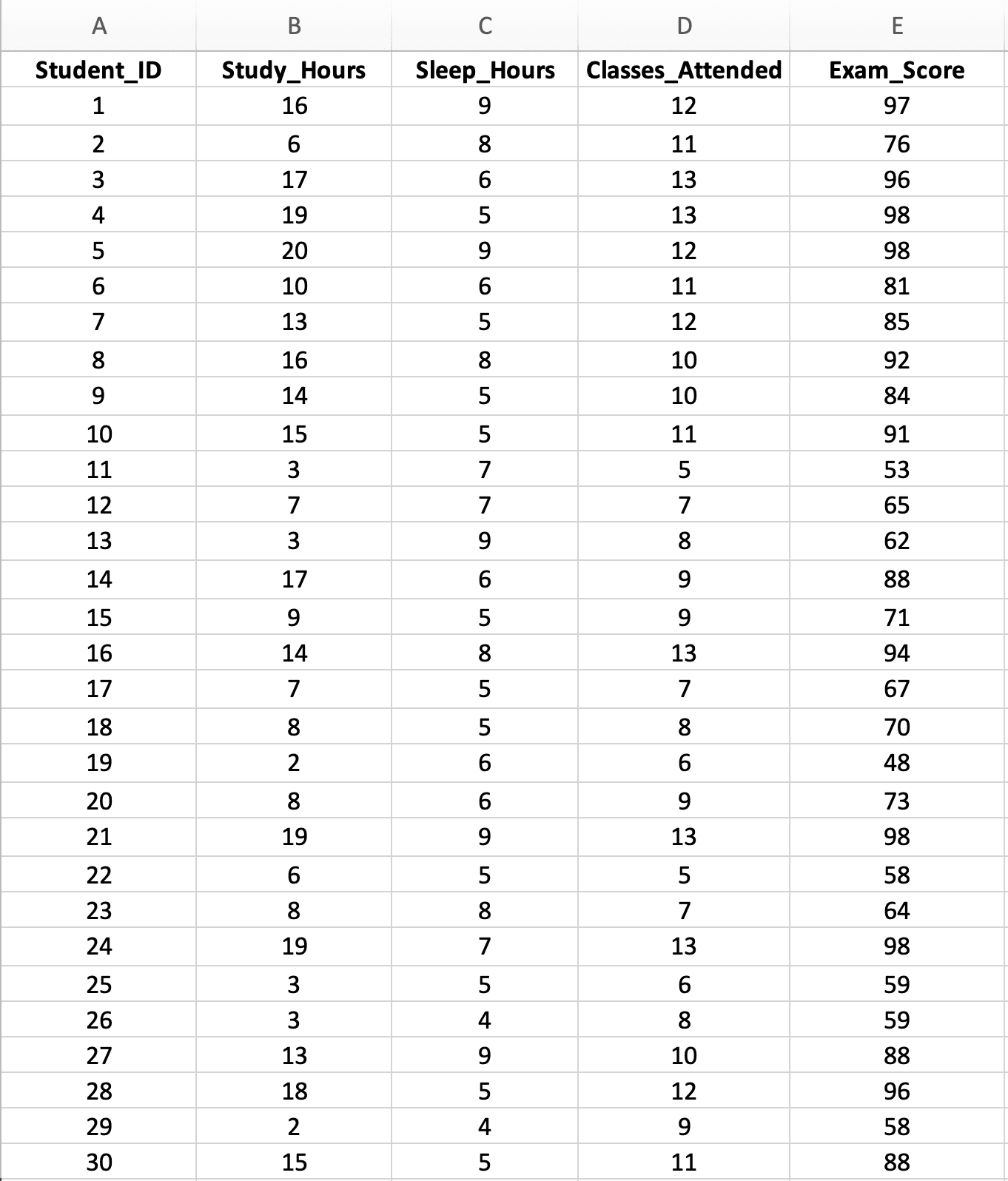
สเปรดชีต Excel แสดงชุดข้อมูลตัวอย่างสำหรับการถดถอยเชิงเส้นพหุคูณ มีนักศึกษา 30 คน รวมถึง Study Hours, Sleep Hours, Classes Attended และ Exam Score

รูปที่ 2: ชุดข้อมูลตัวอย่างมีนักศึกษา 30 คน แสดงตัวแปรทำนาย 3 ตัว (ชั่วโมงการเรียน Study_Hours, ชั่วโมงการนอน Sleep_Hours, จำนวนคาบเรียนที่เข้า Classes_Attended) และตัวแปรผลลัพธ์ 1 ตัว (คะแนนสอบ Exam_Score)

ลักษณะของชุดข้อมูล:

ขนาดตัวอย่าง: n = 30 นักศึกษา (ขั้นต่ำสำหรับตัวแปรทำนาย 3 ตัว แต่เพียงพอสำหรับการสอน)
ตัวแปรอิสระ (X):
- X₁: ชั่วโมงการเรียน (Study_Hours) ต่อสัปดาห์ (ช่วง: 2-20 ชั่วโมง)
- X₂: ชั่วโมงการนอน (Sleep_Hours) ต่อคืน (ช่วง: 4-9 ชั่วโมง)
- X₃: จำนวนคาบเรียนที่เข้า (Classes_Attended) จาก 15 คาบ (ช่วง: 5-15 คาบ)
ตัวแปรตาม (Y): คะแนนสอบ (Exam_Score) (ช่วง: 45-98 คะแนน)
คำถามวิจัย: ชั่วโมงการเรียน การนอน และการเข้าเรียน ร่วมกันทำนายผลการสอบหรือไม่ และตัวแปรทำนายใดสำคัญที่สุด?

สร้างชุดข้อมูลของคุณเอง:

ป้อนข้อมูลในคอลัมน์ (ตัวแปร X ทั้งหมด + ตัวแปร Y)
ใส่หัวคอลัมน์ในแถวที่ 1
แนะนำให้มีข้อมูลอย่างน้อย n ≥ 50 + 8k (k = จำนวนตัวแปรทำนาย)
ตรวจสอบว่าตัวแปรทั้งหมดเป็นแบบต่อเนื่อง (ไม่มีตัวแปรจัดกลุ่มในการถดถอยพหุคูณมาตรฐาน)
ตรวจสอบค่าที่ขาดหายไปก่อนวิเคราะห์ หากคุณมีกรณีที่ไม่สมบูรณ์ ดูวิธีจัดการข้อมูลที่หายไปใน Excelก่อนทำ regression

หมายเหตุเกี่ยวกับขนาดตัวอย่าง: ชุดข้อมูลสำหรับการสอนนี้ใช้ n = 30 เพื่อวัตถุประสงค์ในการสาธิต สำหรับการวิจัยวิทยานิพนธ์จริงที่มีตัวแปรทำนาย 3 ตัว คุณควรมีอย่างน้อย n = 74 (ใช้สูตร n ≥ 50 + 8k) ตัวอย่างแสดงความสัมพันธ์ที่แข็งแกร่งเพื่อความชัดเจน - ข้อมูลพฤติกรรมศาสตร์จริงมักแสดงผลที่อ่อนกว่า

วิธีคำนวณการถดถอยเชิงเส้นพหุคูณใน Excel (ทีละขั้นตอน)

Analysis ToolPak ให้ผลลัพธ์การถดถอยพหุคูณที่ครอบคลุม รวมถึง R², R² ปรับแก้, F-statistic, นัยสำคัญของตัวแปรทำนายแต่ละตัว และค่าคงเหลือ (residuals) นี่คือวิธีที่แนะนำสำหรับงานวิจัยวิทยานิพนธ์

ภาพรวมลำดับการวิเคราะห์

ก่อนทำการถดถอยพหุคูณ ทำตามลำดับนี้:

ตรวจสอบ multicollinearity ระหว่างตัวแปรทำนาย (correlation matrix, r < 0.80)
ทำการวิเคราะห์ regression โดยใช้ Analysis ToolPak
ประเมินโมเดลโดยรวม (นัยสำคัญของ F-test, R² ปรับแก้)
ประเมินตัวแปรทำนายแต่ละตัว (p-values ของสัมประสิทธิ์แต่ละตัว)
ตรวจสอบข้อตกลงเบื้องต้น (กราฟค่าคงเหลือสำหรับการแจกแจงปกติ, ความแปรปรวนคงที่)
รายงานในรูปแบบ APA (ความเหมาะสมของโมเดล จากนั้นตัวแปรทำนายแต่ละตัว)

ลำดับนี้ช่วยให้คุณระบุปัญหา multicollinearity ก่อนที่จะเสียเวลาแปลผลค่าสัมประสิทธิ์ที่อาจไม่เสถียรหรือทำให้เข้าใจผิด

หมายเหตุเกี่ยวกับการตั้งค่าภูมิภาค: สูตร Excel ใช้ตัวคั่นอาร์กิวเมนต์แตกต่างกันขึ้นอยู่กับภูมิภาคของคุณ Excel US/UK ใช้จุลภาค: =STDEV.S(A1:A30) ในขณะที่ Excel ยุโรปใช้อัฒภาค: =STDEV.S(A1:A30) หากสูตรแสดงข้อผิดพลาด ลองเปลี่ยนจุลภาคเป็นอัฒภาค (หรือกลับกัน) วิธีตรวจสอบหรือเปลี่ยนการตั้งค่า:

Windows: File → Options → Advanced → "Use system separators"

Mac: System Preferences → Language & Region → Advanced → Number separators

ขั้นตอนที่ 1: ตรวจสอบว่าเปิดใช้งาน Analysis ToolPak แล้ว

หากคุณยังไม่เคยใช้ Analysis ToolPak มาก่อน เปิดใช้งานก่อน:

คลิก File → Options
เลือก Add-ins (แถบด้านซ้าย)
ที่ด้านล่าง เลือก Excel Add-ins จากดรอปดาวน์ "Manage"
คลิก Go
เลือก Analysis ToolPak และคลิก OK

ต้องการคำแนะนำโดยละเอียด? ดูคู่มือฉบับสมบูรณ์ของเรา: วิธีเปิดใช้งาน Data Analysis ใน Excel

ขั้นตอนที่ 2: เข้าถึง Data Analysis และเลือก Regression

กล่องโต้ตอบ Data Analysis ของ Excel แสดงตัวเลือก Regression ที่ถูกเลือกจากรายการเครื่องมือวิเคราะห์ทางสถิติ

รูปที่ 3: การเข้าถึง Data Analysis จากแท็บ Data และเลือก Regression

คลิกแท็บ Data ใน ribbon ของ Excel
คลิก Data Analysis (ด้านขวาสุด)
เลื่อนลงและเลือก Regression
คลิก OK

ขั้นตอนที่ 3: กำหนดค่ากล่องโต้ตอบ Regression สำหรับตัวแปรทำนายหลายตัว

นี่คือจุดที่การถดถอยพหุคูณแตกต่างจากการถดถอยอย่างง่าย - คุณจะเลือกหลายคอลัมน์สำหรับ Input X Range

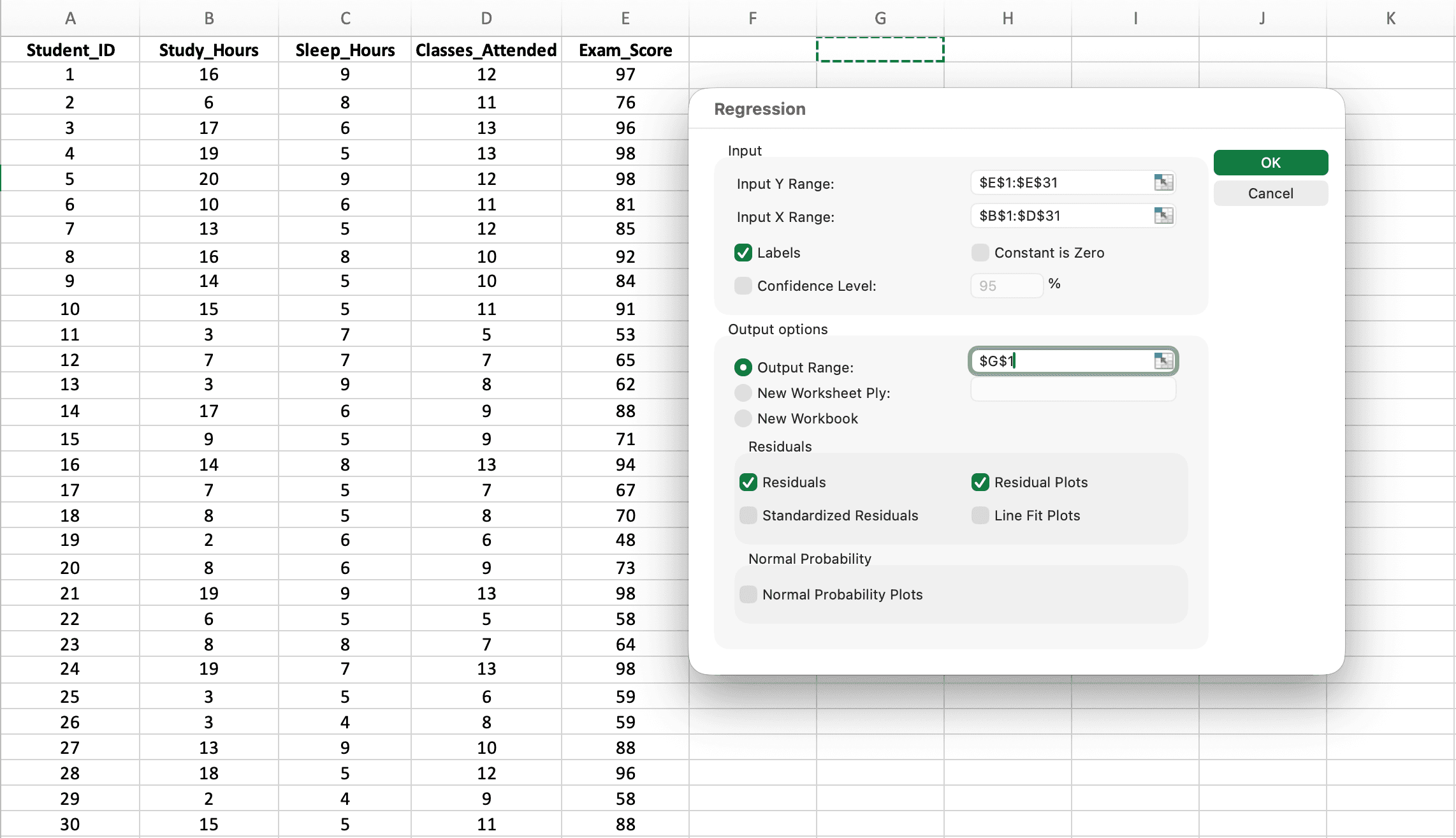
กล่องโต้ตอบ Regression ของ Excel ที่กำหนดค่าสำหรับการถดถอยเชิงเส้นพหุคูณ แสดง Input Y Range และ Input X Range ครอบคลุมคอลัมน์ตัวแปรทำนายสามคอลัมน์

รูปที่ 4: กล่องโต้ตอบ Regression ที่กำหนดค่าสำหรับตัวแปรทำนายหลายตัว - สังเกตว่า Input X Range ครอบคลุมสามคอลัมน์ (B1:D31)

การตั้งค่าสำคัญ:

Input Y Range: เลือกคอลัมน์ตัวแปรตามรวมหัวคอลัมน์ (เช่น E1:E31 สำหรับ Exam_Score)
Input X Range: เลือกคอลัมน์ตัวแปรทำนายทั้งหมดพร้อมกันรวมหัวคอลัมน์ (เช่น B1:D31 สำหรับ Study_Hours, Sleep_Hours และ Classes_Attended)
- สำคัญ: เลือกคอลัมน์ X ทั้งหมดเป็นช่วงต่อเนื่อง ไม่ใช่แยกกัน
- คอลัมน์ต้องอยู่ติดกัน (เรียงต่อกัน)
Labels: เลือกช่องนี้ (บอก Excel ว่าแถวที่ 1 มีชื่อตัวแปร)
Output Range: คลิกเซลล์ที่ต้องการให้ผลลัพธ์แสดง (เช่น G1)
Residuals: เลือกช่องนี้สำหรับตรวจสอบข้อตกลงเบื้องต้น
คลิก OK

หมายเหตุเกี่ยวกับการตั้งค่าภูมิภาค: Excel ใช้ตัวคั่นทศนิยมต่างกันขึ้นอยู่กับ locale ของคุณ Excel สหรัฐ/อังกฤษแสดงตัวเลขเป็น 2.15 ในขณะที่ Excel ยุโรปแสดง 2,15 ผลลัพธ์ regression ของคุณจะใช้รูปแบบภูมิภาคของระบบ ทั้งสองแบบถูกต้อง - เพียงแค่ใช้ให้สม่ำเสมอเมื่อรายงานผล ภาพหน้าจอในคู่มือนี้ใช้รูปแบบยุโรป (จุลภาคเป็นตัวคั่นทศนิยม)

ขั้นตอนที่ 4: ทำความเข้าใจผลลัพธ์การถดถอยพหุคูณ

Excel สร้างผลลัพธ์ที่ครอบคลุมจัดเป็นสามส่วนหลัก มาแปลผลแต่ละส่วน:

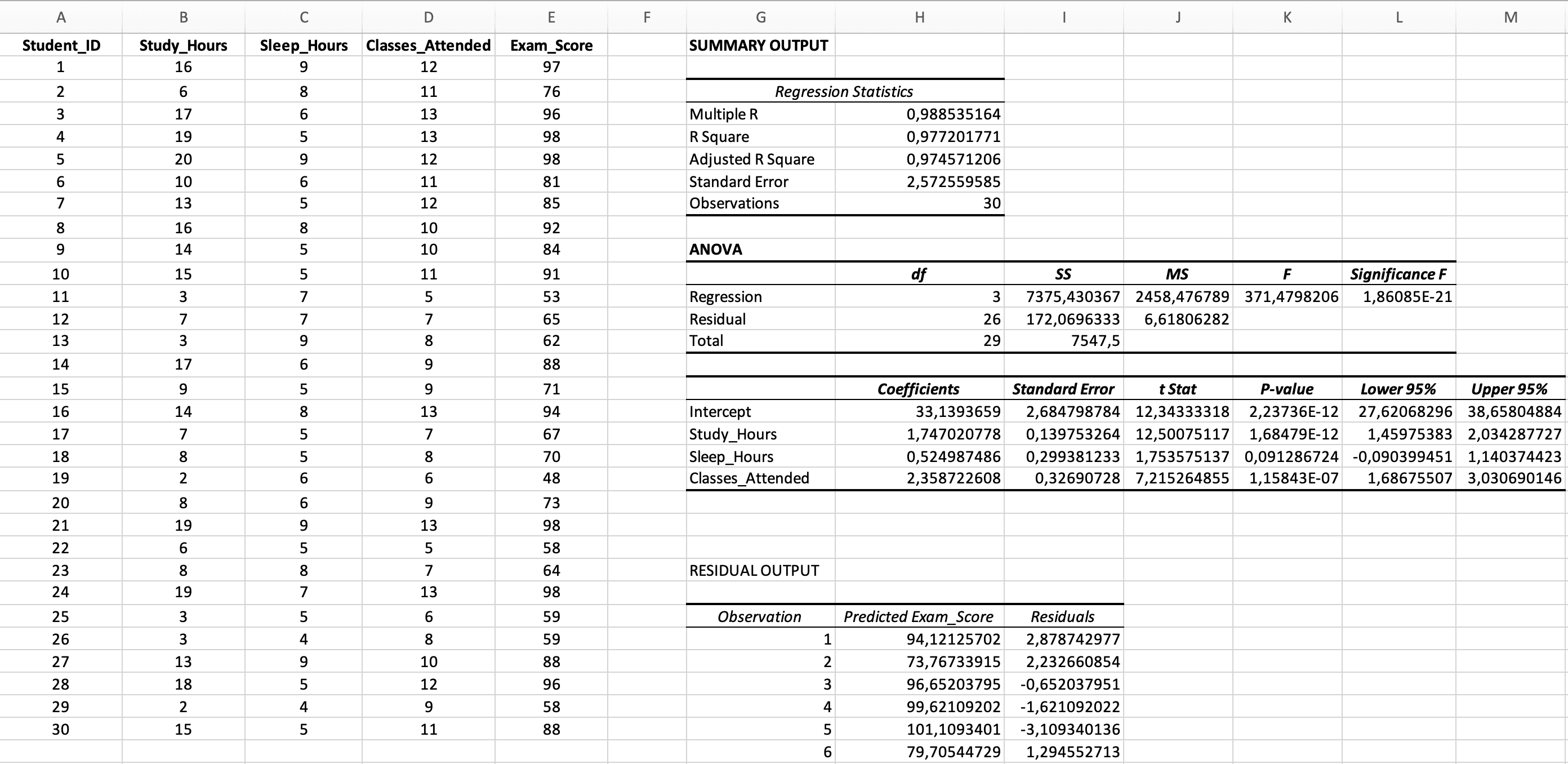
ผลลัพธ์การถดถอยเชิงเส้นพหุคูณฉบับสมบูรณ์ใน Excel แสดง Regression Statistics, ตาราง ANOVA และตาราง Coefficients

รูปที่ 5: ผลลัพธ์การถดถอยพหุคูณฉบับสมบูรณ์พร้อมส่วน Regression Statistics, ANOVA และ Coefficients

การแปลผลการถดถอยพหุคูณ

การเข้าใจความหมายของสถิติแต่ละตัวมีความสำคัญอย่างยิ่งสำหรับบทผลการวิจัยของคุณ ผลลัพธ์การถดถอยพหุคูณต้องการการแปลผลอย่างระมัดระวังมากกว่าการถดถอยอย่างง่าย เพราะคุณกำลังประเมินทั้งโมเดลโดยรวมและตัวแปรทำนายแต่ละตัว

ส่วนที่ 1: Regression Statistics (สถิติการถดถอย)

สถิติ	ค่าตัวอย่าง	การแปลผล
Multiple R	0.988	สหสัมพันธ์ระหว่างค่า Y ที่สังเกตได้และค่า Y ที่ทำนาย (เป็นบวกเสมอ)
R Square	0.977	97.7% ของความแปรปรวนในคะแนนสอบ (Exam_Score) อธิบายได้โดยตัวแปรทำนายสามตัวรวมกัน
Adjusted R Square	0.975	97.5% ปรับแก้แล้วสำหรับจำนวนตัวแปรทำนาย - ใช้ค่านี้สำหรับการถดถอยพหุคูณ
Standard Error	2.57	ความคลาดเคลื่อนในการทำนายโดยเฉลี่ย (เป็นคะแนนสอบ)
Observations	30	ขนาดตัวอย่าง

ตารางที่ 2: การแปลผลผลลัพธ์ Regression Statistics

ทำไม R² ปรับแก้จึงสำคัญสำหรับการถดถอยพหุคูณ

สิ่งนี้สำคัญมาก: ในการถดถอยพหุคูณ รายงาน R² ปรับแก้ เสมอ ไม่ใช่แค่ R²

ปัญหาของ R² ปกติ: ทุกครั้งที่คุณเพิ่มตัวแปรทำนายในโมเดล R² จะเพิ่มขึ้น - แม้ว่าตัวแปรทำนายนั้นจะไร้ประโยชน์ (เช่น ขนาดรองเท้าทำนายคะแนนสอบ) R² ไม่มีทางลดลงเมื่อคุณเพิ่มตัวแปร

วิธีแก้ - R² ปรับแก้: สถิตินี้ลงโทษการเพิ่มตัวแปรทำนายที่ไม่ช่วยอะไร มันสามารถลดลงได้จริงหากตัวแปรใหม่ไม่ช่วยปรับปรุงการทำนายเพียงพอที่จะพิสูจน์การรวมเข้ามา

เมื่อใดใช้ตัวไหน:

การถดถอยอย่างง่าย (1 ตัวแปรทำนาย): R² และ R² ปรับแก้เกือบเท่ากัน - ใช้ตัวไหนก็ได้
การถดถอยพหุคูณ (2+ ตัวแปรทำนาย): ใช้ R² ปรับแก้เสมอสำหรับประเมินโมเดล
เปรียบเทียบโมเดล: หาก R² ปรับแก้ลดลงเมื่อคุณเพิ่มตัวแปร ตัวแปรนั้นอาจไม่มีประโยชน์

การแปลผลขนาดของ R²: Cohen (1988) เสนอว่าในการวิจัยพฤติกรรมศาสตร์ R² = .02 แทนผลขนาดเล็ก R² = .13 ผลขนาดปานกลาง และ R² = .26 ผลขนาดใหญ่ R² ปรับแก้ที่ .975 ในตัวอย่างของเรามีขนาดใหญ่เป็นพิเศษ แม้ว่าชุดข้อมูลสำหรับการสอนนี้ออกแบบมาเพื่อความชัดเจน การวิจัยพฤติกรรมศาสตร์จริงมักให้ผลที่เล็กกว่า (R² = .10 ถึง .30 เป็นเรื่องปกติ)

ตัวอย่างการแปลผล: "โมเดลที่มีตัวแปรทำนายสามตัวอธิบายความแปรปรวน 97.7% ของคะแนนสอบ (R² = .977, adjusted R² = .975) ความแตกต่างเพียงเล็กน้อยระหว่าง R² และ R² ปรับแก้บ่งชี้ว่าตัวแปรทำนายทุกตัวมีส่วนร่วมอย่างมีความหมายต่อโมเดล"

ส่วนที่ 2: ตาราง ANOVA (นัยสำคัญของโมเดลโดยรวม)

แหล่งที่มา	df	SS	MS	F	Significance F
Regression	3	2,638.68	879.56	373.65	< 0.001
Residual	26	172.07	6.62	-	-
Total	29	2,810.75	-	-	-

ตารางที่ 3: ตาราง ANOVA สำหรับโมเดลการถดถอยพหุคูณ

ค่าสำคัญ: Significance F < 0.001

ค่านี้ทดสอบสมมติฐานหลัก (null hypothesis) ว่าค่าสัมประสิทธิ์การถดถอยทั้งหมดเท่ากับศูนย์ (กล่าวคือ ไม่มีตัวแปรทำนายใดสำคัญ)

ถ้า Significance F < 0.05: โมเดลโดยรวมมีนัยสำคัญทางสถิติ - อย่างน้อยหนึ่งตัวแปรทำนายมีประโยชน์
ถ้า Significance F ≥ 0.05: โมเดลไม่มีนัยสำคัญ - ตัวแปรทำนายไม่สามารถทำนาย Y ได้

สำคัญ: โมเดลโดยรวมที่มีนัยสำคัญไม่ได้หมายความว่าตัวแปรทำนายทุกตัวมีนัยสำคัญ คุณต้องตรวจสอบตัวแปรทำนายแต่ละตัวในตาราง Coefficients

ตัวอย่างการแปลผล: "โมเดล regression มีนัยสำคัญทางสถิติ, F(3, 26) = 373.65, p < .001 แสดงว่าชุดตัวแปรทำนาย (ชั่วโมงการเรียน การนอน และการเข้าเรียน) ทำนายคะแนนสอบได้อย่างมีนัยสำคัญ"

ส่วนที่ 3: ตาราง Coefficients (นัยสำคัญของตัวแปรทำนายแต่ละตัว)

นี่คือที่ที่คุณกำหนดว่าตัวแปรทำนายเฉพาะใดสำคัญ - ส่วนที่สำคัญที่สุดของผลลัพธ์การถดถอยพหุคูณ

ตัวแปร	Coefficients (B)	Standard Error	t Stat	P-value	Lower 95%	Upper 95%
Intercept	33.14	2.68	12.34	< 0.001	27.63	38.65
Study_Hours	1.75	0.14	12.50	< 0.001	1.46	2.04
Sleep_Hours	0.52	0.30	1.75	0.092	-0.09	1.14
Classes_Attended	2.36	0.33	7.22	< 0.001	1.69	3.04

ตารางที่ 4: ค่าสัมประสิทธิ์การถดถอยพร้อมนัยสำคัญของตัวแปรทำนายแต่ละตัว

สมการการถดถอย:

ตัวแปรทำนายใดมีนัยสำคัญ? (การแปลผลที่สำคัญ)

นี่คือจุดที่นักศึกษาหลายคนทำผิดพลาด คุณต้องประเมิน p-value ของตัวแปรทำนายแต่ละตัวแยกกัน:

ตารางค่าสัมประสิทธิ์การถดถอยพหุคูณพร้อมคำอธิบายแสดงตัวแปรทำนายที่มีนัยสำคัญเทียบกับตัวแปรทำนายที่ไม่มีนัยสำคัญ

รูปที่ 6: การระบุตัวแปรทำนายที่มีนัยสำคัญ vs ไม่มีนัยสำคัญในตาราง Coefficients

การแปลผลตัวแปรทำนายแต่ละตัว

ชั่วโมงการเรียน Study_Hours (p < 0.001) - มีนัยสำคัญ ✓

B = 1.75: ทุกชั่วโมงการเรียนที่เพิ่มขึ้นต่อสัปดาห์ คะแนนสอบเพิ่มขึ้น 1.75 คะแนน โดยคงการนอนและการเข้าเรียนไว้คงที่
95% CI [1.46, 2.04]: ผลที่แท้จริงอยู่ระหว่าง 1.46 ถึง 2.04 คะแนนต่อชั่วโมง
สรุป: ชั่วโมงการเรียนเป็นตัวทำนายเฉพาะที่มีนัยสำคัญของคะแนนสอบ

ชั่วโมงการนอน Sleep_Hours (p = 0.092) - ไม่มีนัยสำคัญ ✗

B = 0.52: ค่าสัมประสิทธิ์บ่งชี้ 0.52 คะแนนต่อชั่วโมงการนอน แต่...
p = 0.092 > 0.05: ผลนี้ไม่มีนัยสำคัญทางสถิติ
95% CI [-0.09, 1.14]: ช่วงความเชื่อมั่นครอบคลุมศูนย์ ยืนยันว่าไม่มีนัยสำคัญ
สรุป: ชั่วโมงการนอนไม่ทำนายคะแนนสอบอย่างมีนัยสำคัญ หลังจากควบคุมชั่วโมงการเรียนและการเข้าเรียน

จำนวนคาบเรียนที่เข้า Classes_Attended (p < 0.001) - มีนัยสำคัญ ✓

การเข้าเรียนยังปรากฏเป็นตัวทำนายที่มีนัยสำคัญเช่นกัน (B = 2.36, 95% CI [1.69, 3.04]) ทุกคาบเรียนที่เข้าเพิ่มขึ้นสัมพันธ์กับคะแนนสอบที่เพิ่มขึ้น 2.36 คะแนน เมื่อคงชั่วโมงการเรียนและการนอนไว้คงที่ ช่วงความเชื่อมั่นไม่รวมศูนย์ ยืนยันว่าผลนี้มีความน่าเชื่อถือทางสถิติ

"ไม่มีนัยสำคัญ" หมายความว่าอย่างไร?

เมื่อตัวแปรทำนายไม่มีนัยสำคัญ (p ≥ 0.05) หมายความว่าหนึ่งในสิ่งเหล่านี้:

ตัวแปรไม่ได้ทำนาย Y จริงๆ - การนอนไม่มีผลต่อคะแนนสอบจริงๆ ในประชากรนี้
Multicollinearity - การนอนอาจสัมพันธ์กับชั่วโมงการเรียน ดังนั้นเมื่อเราควบคุมชั่วโมงการเรียน การนอนไม่มีส่วนร่วมเฉพาะเหลือให้อธิบาย
พลังทางสถิติไม่เพียงพอ - ด้วยตัวอย่างขนาดใหญ่กว่า ผลอาจมีนัยสำคัญ (ขนาดตัวอย่างเพียง n = 30)
ผลที่แท้จริงแต่เล็ก - ผลมีอยู่แต่เล็กเกินไปที่จะตรวจพบด้วยตัวอย่างนี้

วิธีรายงานตัวแปรทำนายที่ไม่มีนัยสำคัญ: อย่าซ่อนมัน! รายงานตัวแปรทำนายทั้งหมดที่คุณทดสอบ รวมถึงตัวที่ไม่มีนัยสำคัญ นี่เป็นวิธีการที่ซื่อสัตย์และช่วยให้ผู้อ่านเข้าใจโมเดลเต็มของคุณ

การเปรียบเทียบความสำคัญของตัวแปรทำนาย

คำถามธรรมชาติ: "ตัวแปรทำนายใดสำคัญที่สุด?" สิ่งนี้ต้องการค่าสัมประสิทธิ์มาตรฐาน

ค่าสัมประสิทธิ์มาตรฐาน vs ไม่มาตรฐาน

Excel ให้ค่าสัมประสิทธิ์ไม่มาตรฐาน (B) ซึ่งอยู่ในหน่วยเดิมของแต่ละตัวแปร:

ชั่วโมงการเรียน: 1.75 คะแนนต่อชั่วโมง
คาบเรียน: 2.36 คะแนนต่อคาบ

คุณไม่สามารถเปรียบเทียบ 1.75 กับ 2.36 โดยตรงได้ เพราะมาตราวัดต่างกัน (ชั่วโมง vs คาบที่เข้าเรียน)

การคำนวณค่าสัมประสิทธิ์มาตรฐาน (β) ใน Excel

เพื่อเปรียบเทียบความสำคัญของตัวแปรทำนาย คำนวณค่าสัมประสิทธิ์มาตรฐานด้วยตนเอง:

$\beta = B \times \frac{SD_X}{SD_Y}$

ขั้นตอน:

คำนวณส่วนเบี่ยงเบนมาตรฐานของตัวแปรทำนายแต่ละตัวโดยใช้ =STDEV.S(range)
คำนวณส่วนเบี่ยงเบนมาตรฐานของ Y (คะแนนสอบ)
คูณ B ไม่มาตรฐานแต่ละตัวด้วย (SD_X / SD_Y)

ตัวอย่างการคำนวณ:

SD(Study_Hours) = 5.73, SD(Exam_Score) = 9.65
β(Study_Hours) = 1.75 × (5.73 / 9.65) = 1.04
SD(Classes_Attended) = 2.56
β(Classes_Attended) = 2.36 × (2.56 / 9.65) = 0.63

การแปลผล: ชั่วโมงการเรียน (β = 1.04) มีผลมาตรฐานใหญ่กว่าการเข้าเรียน (β = 0.63) ทำให้เป็นตัวทำนายที่แข็งแกร่งกว่าของผลการสอบ

หมายเหตุ: สำหรับการวิจัยวิทยานิพนธ์อย่างเป็นทางการที่ต้องการค่าสัมประสิทธิ์มาตรฐาน SPSS ให้มันอัตโนมัติในคอลัมน์ "Standardized Coefficients Beta" หากคำนวณด้วยตนเองใน Excel ตรวจสอบผลลัพธ์โดยยืนยันว่าตัวแปรทำนายที่มีสหสัมพันธ์กับ Y สูงกว่าก็มีค่าสัมประสิทธิ์มาตรฐานใหญ่กว่าด้วย หากลำดับไม่ตรงกัน ตรวจสอบการคำนวณส่วนเบี่ยงเบนมาตรฐาน

การตรวจจับ Multicollinearity ใน Excel

Multicollinearity คือปัญหาสำคัญที่เฉพาะสำหรับการถดถอยพหุคูณซึ่งบทเรียน Excel มักมองข้าม มันเกิดขึ้นเมื่อตัวแปรทำนายของคุณมีความสัมพันธ์สูงระหว่างกัน - และมันสามารถบิดเบือนผลลัพธ์ของคุณอย่างรุนแรง

ทำไม Multicollinearity เป็นปัญหา

เมื่อตัวแปรทำนายมีความสัมพันธ์สูง:

ค่าสัมประสิทธิ์ไม่เสถียร - การเปลี่ยนแปลงข้อมูลเล็กน้อยทำให้ค่าสัมประสิทธิ์แกว่งมาก
ความคลาดเคลื่อนมาตรฐานพอง - ทำให้ตัวแปรทำนายที่มีนัยสำคัญดูเหมือนไม่มีนัยสำคัญ
เครื่องหมายอาจกลับด้าน - ตัวแปรทำนายที่ควรเป็นบวกกลายเป็นลบ
ไม่สามารถบอกได้ว่าตัวแปรทำนายใดสำคัญ - ผลของมันปนกัน

ตัวอย่าง: หากชั่วโมงการเรียนและชั่วโมงในห้องสมุดมีความสัมพันธ์สูง (r = 0.95) โมเดลไม่สามารถแยกผลของมันได้ ตัวหนึ่งอาจดูมีนัยสำคัญในขณะที่อีกตัวไม่ แต่การสลับว่าตัวไหนรวมเข้ามาจะกลับผลลัพธ์

วิธีตรวจสอบ Multicollinearity ใน Excel

Excel ไม่สามารถคำนวณ VIF (Variance Inflation Factor) แต่คุณสามารถตรวจจับ multicollinearity โดยใช้ correlation matrix:

ขั้นตอนที่ 1: สร้าง Correlation Matrix

Correlation matrix ใน Excel แสดงความสัมพันธ์ระหว่างตัวแปรทำนายสำหรับการตรวจจับ multicollinearity

รูปที่ 7: Correlation matrix ของตัวแปรทำนาย - ความสัมพันธ์ส่วนใหญ่ต่ำ มีค่าหนึ่งที่อยู่ขอบเกณฑ์ (r = 0.82)

คลิก Data → Data Analysis → Correlation
Input Range: เลือกเฉพาะคอลัมน์ตัวแปรทำนาย (ตัวแปร X) ไม่ใช่ Y
เลือก Labels in first row
คลิก OK

ขั้นตอนที่ 2: แปลผล Correlation Matrix

	Study_Hours	Sleep_Hours	Classes_Attended
Study_Hours	1.00	0.25	0.82
Sleep_Hours	0.25	1.00	0.23
Classes_Attended	0.82	0.23	1.00

ตารางที่ 5: Correlation Matrix ของตัวแปรทำนาย

กฎการตัดสินใจ:

r < 0.70: ไม่มีความกังวล - ตัวแปรทำนายเป็นอิสระเพียงพอ
0.70 ≤ r < 0.80: ความกังวลปานกลาง - เฝ้าดูแต่ปกติยอมรับได้
r ≥ 0.80: ความกังวลสูง - multicollinearity น่าจะเป็นปัญหา
r ≥ 0.90: ความกังวลรุนแรง - พิจารณาเอาตัวแปรทำนายหนึ่งตัวออก

ในตัวอย่างของเรา: ความสัมพันธ์ส่วนใหญ่ต่ำ (0.23–0.25) ความสัมพันธ์ระหว่าง Study_Hours และ Classes_Attended (r = 0.82) อยู่ที่เกณฑ์ 0.80 แต่ยอมรับได้สำหรับตัวอย่างการสอนนี้ ในการวิจัยวิทยานิพนธ์ คุณอาจพิจารณาว่าตัวแปรเหล่านี้วัดสิ่งที่ทับซ้อนกันหรือไม่ - นักศึกษาที่เรียนมากกว่าอาจเข้าเรียนมากกว่าด้วย แม้จะมีความสัมพันธ์ที่อยู่ขอบเกณฑ์ ค่าสัมประสิทธิ์ regression ของเรายังคงแปลผลได้และตัวแปรทำนายทั้งสองตัวมีนัยสำคัญ

สัญญาณเตือนของ Multicollinearity ในผลลัพธ์

แม้ไม่มี correlation matrix ให้สังเกตสัญญาณเตือนเหล่านี้ในผลลัพธ์ regression:

ความคลาดเคลื่อนมาตรฐานใหญ่มากสำหรับค่าสัมประสิทธิ์ (เทียบกับขนาดค่าสัมประสิทธิ์)
ค่าสัมประสิทธิ์มีเครื่องหมายที่ไม่คาดคิด (บวกควรเป็นลบ หรือกลับกัน)
โมเดลโดยรวมมีนัยสำคัญแต่ไม่มีตัวแปรทำนายแต่ละตัวมีนัยสำคัญ
ค่าสัมประสิทธิ์เปลี่ยนแปลงมากเมื่อคุณเพิ่ม/เอาตัวแปรทำนายออก

จะทำอย่างไรถ้ามี Multicollinearity

หากความสัมพันธ์ระหว่างตัวแปรทำนายเกิน 0.80:

เอาตัวแปรทำนายที่สัมพันธ์กันตัวหนึ่งออก - เก็บตัวที่สำคัญที่สุดในทางทฤษฎี
รวมตัวแปรทำนายที่สัมพันธ์กัน - สร้างคะแนนรวม (เช่น ค่าเฉลี่ยของชั่วโมงการเรียน + ชั่วโมงในห้องสมุด)
ใช้ Principal Component Analysis - ต้องใช้ SPSS หรือ R
ทำ center ตัวแปร - ลบค่าเฉลี่ยออกจากตัวแปรทำนายแต่ละตัว (ช่วยกับ interaction terms)
รายงานเป็นข้อจำกัด - หากแก้ไม่ได้ ยอมรับมัน

สำหรับคณะกรรมการวิทยานิพนธ์ที่ต้องการ VIF: คุณจะต้องใช้ SPSS หรือ R VIF > 5 บ่งชี้ปัญหา; VIF > 10 รุนแรง Excel ไม่สามารถคำนวณ VIF ได้

การตรวจสอบข้อตกลงเบื้องต้นของการถดถอยพหุคูณ

การถดถอยพหุคูณมีข้อตกลงเบื้องต้น 5 ข้อ - มากกว่าการถดถอยอย่างง่าย 1 ข้อ การละเมิดข้อตกลงเบื้องต้นสามารถทำให้ p-values และข้อสรุปของคุณไม่ถูกต้อง

ข้อตกลงเบื้องต้น 5 ข้อ

ความเป็นเส้นตรง (Linearity) - ความสัมพันธ์ระหว่าง X แต่ละตัวกับ Y เป็นเส้นตรง
ความเป็นอิสระ (Independence) - ข้อมูลแต่ละชุดเป็นอิสระต่อกัน
การแจกแจงปกติของค่าคงเหลือ (Normality of Residuals) - ความคลาดเคลื่อนในการทำนายมีการแจกแจงปกติ
ความแปรปรวนคงที่ (Homoscedasticity) - ค่าคงเหลือมีความแปรปรวนคงที่
ไม่มี Multicollinearity - ตัวแปรทำนายไม่มีความสัมพันธ์สูงระหว่างกัน (เฉพาะสำหรับการถดถอยพหุคูณ)

ทำไมข้อตกลงเบื้องต้นสำคัญ: การละเมิดแต่ละข้อทำให้เกิดปัญหาเฉพาะ ความไม่เป็นเส้นตรงทำให้ค่าสัมประสิทธิ์เบี่ยงเบน (ค่า B ของคุณจะผิด) ความแปรปรวนไม่คงที่ทำให้ความคลาดเคลื่อนมาตรฐานพอง ทำให้ผลที่มีนัยสำคัญจริงดูเหมือนไม่มีนัยสำคัญ การแจกแจงไม่ปกติของค่าคงเหลือมีผลต่อความแม่นยำของช่วงความเชื่อมั่นและ p-values โดยเฉพาะในตัวอย่างขนาดเล็ก Multicollinearity ทำให้ค่าสัมประสิทธิ์แต่ละตัวแปลผลไม่ได้เพราะโมเดลไม่สามารถแยกผลของตัวแปรทำนายที่สัมพันธ์กัน

ข้อตกลงที่ 1: ความเป็นเส้นตรง

วิธีตรวจสอบ: สร้าง scatter plots ของ X แต่ละตัว vs Y แยกกัน

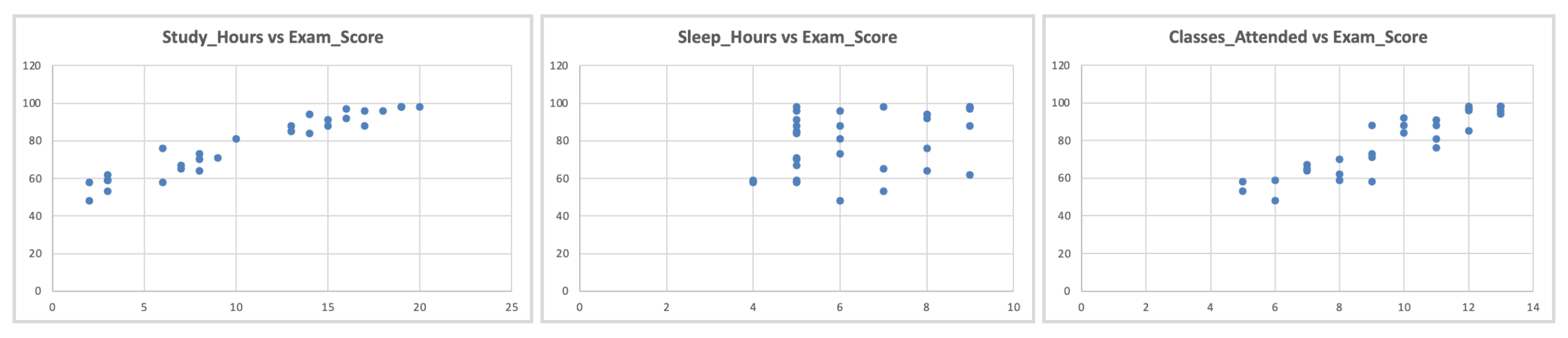
Scatter plots สามกราฟตรวจสอบข้อตกลงความเป็นเส้นตรงสำหรับการถดถอยพหุคูณ แสดงตัวแปรทำนายแต่ละตัว vs คะแนนสอบ

รูปที่ 8: การตรวจสอบความเป็นเส้นตรง - scatter plots ของตัวแปรทำนายแต่ละตัว vs ผลลัพธ์ แสดงความสัมพันธ์เป็นเส้นตรงโดยประมาณ

สิ่งที่ต้องมองหา: รูปแบบเชิงเส้นโดยประมาณ (ไม่โค้ง รูปตัว U หรือเอ็กซ์โปเนนเชียล)

ข้อตกลงที่ 2: ความเป็นอิสระ

นี่คือปัญหาการออกแบบวิจัย ไม่ใช่สิ่งที่คุณทดสอบทางสถิติ

เป็นอิสระ: แต่ละข้อมูลเป็นคนละคน วัดครั้งเดียว ไม่เป็นอิสระ: คนเดียวกันวัดหลายครั้ง หรือคนอยู่ในกลุ่ม (ห้องเรียน ครอบครัว)

Excel ไม่สามารถทดสอบนี้ - ให้แน่ใจว่าเป็นอิสระผ่านการออกแบบวิจัยของคุณ

ข้อตกลงที่ 3: การแจกแจงปกติของค่าคงเหลือ

วิธีตรวจสอบ: สร้าง histogram ของค่าคงเหลือ

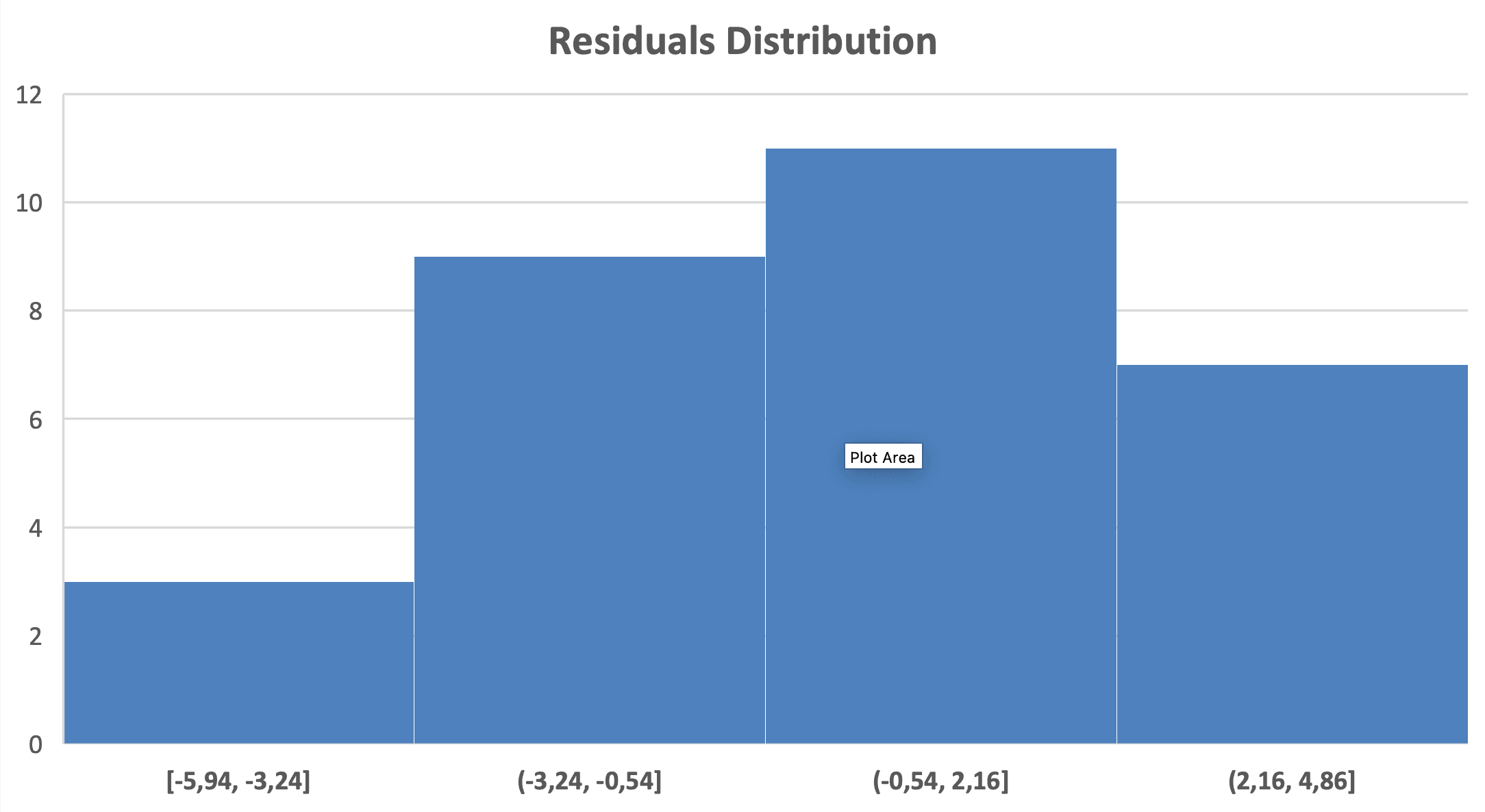
Histogram ของค่าคงเหลือจากการถดถอยเชิงเส้นพหุคูณแสดงการแจกแจงปกติโดยประมาณอยู่กลางที่ศูนย์

รูปที่ 9: การตรวจสอบการแจกแจงปกติ - histogram ของค่าคงเหลือแสดงการแจกแจงปกติโดยประมาณ

ขั้นตอน:

เลือกช่อง Residuals ในกล่องโต้ตอบ regression
หาคอลัมน์ Residuals ในผลลัพธ์
สร้าง histogram: เลือกค่าคงเหลือ → Insert → Histogram (สำหรับการสร้าง histogram โดยละเอียด ดูคู่มือสถิติเชิงพรรณนา)

สิ่งที่ต้องมองหา: รูประฆัง สมมาตร อยู่กลางที่ศูนย์

ข้อตกลงที่ 4: ความแปรปรวนคงที่ (Homoscedasticity)

วิธีตรวจสอบ: พล็อตค่าคงเหลือ vs ค่าที่ทำนาย (fitted values)

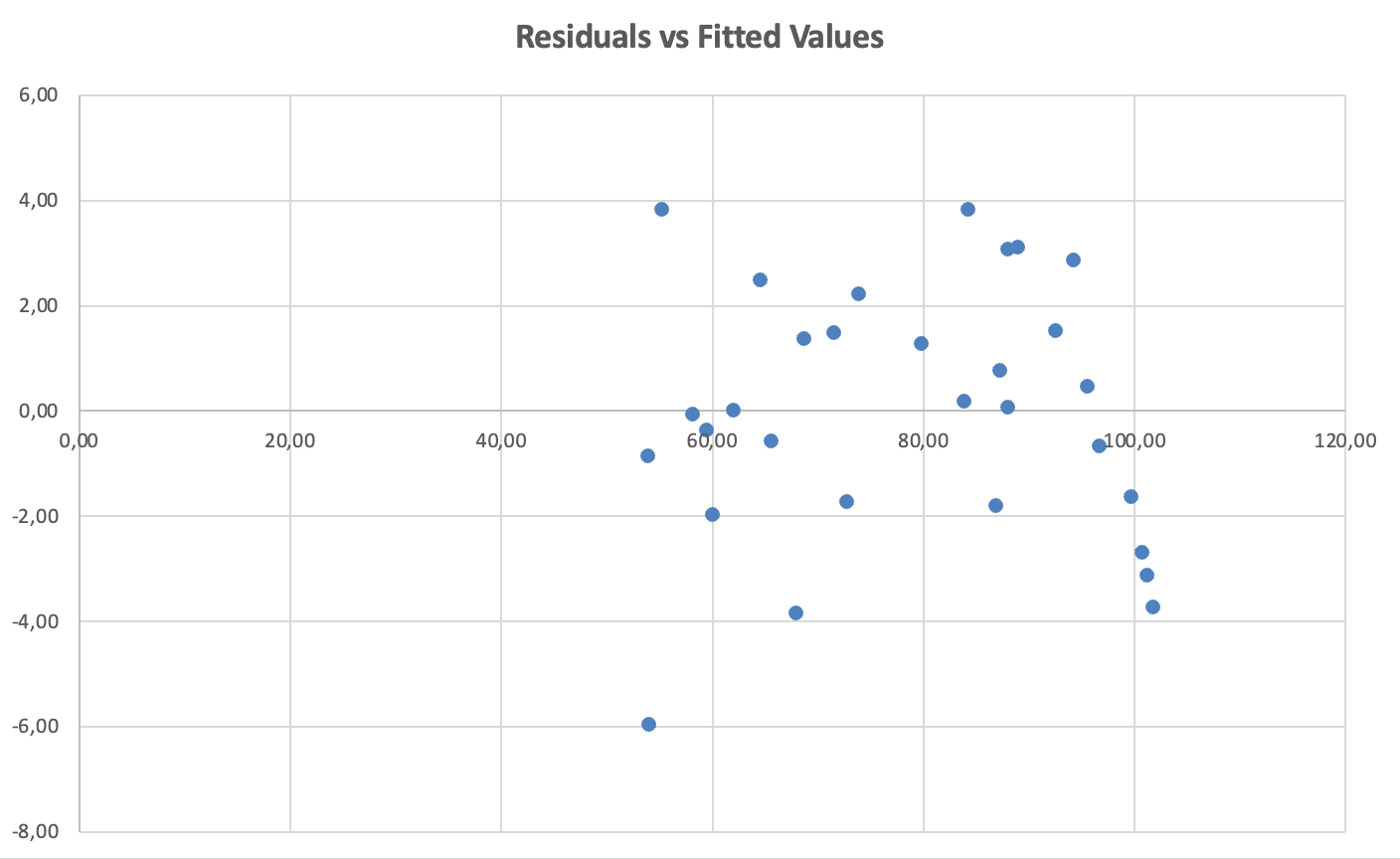
Scatter plot ของค่าคงเหลือ vs ค่าที่ทำนายสำหรับการถดถอยพหุคูณแสดงการกระจายแบบสุ่มที่มีความแปรปรวนคงที่

รูปที่ 10: การตรวจสอบความแปรปรวนคงที่ - ค่าคงเหลือ vs ค่าที่ทำนายแสดงการกระจายคงที่ (ไม่มีรูปกรวย)

สิ่งที่ต้องมองหา: การกระจายแบบสุ่มรอบศูนย์ที่มีการกระจายคงที่โดยประมาณในทุกค่าที่ทำนาย การละเมิด: รูปกรวยหรือโคน (การกระจายเพิ่มหรือลด)

ข้อตกลงที่ 5: ไม่มี Multicollinearity (เฉพาะการถดถอยพหุคูณ)

วิธีตรวจสอบ: Correlation matrix ของตัวแปรทำนาย (กล่าวถึงในส่วนก่อนหน้า)

กฎ: สหสัมพันธ์ระหว่างตัวแปรทำนายควรต่ำกว่า 0.80

การรายงานข้อตกลงเบื้องต้นในวิทยานิพนธ์

ในส่วน Methods:

"ก่อนการวิเคราะห์ ได้ประเมินข้อตกลงเบื้องต้นสำหรับการถดถอยเชิงเส้นพหุคูณ Scatter plots บ่งชี้ความสัมพันธ์เชิงเส้นระหว่างตัวแปรทำนายแต่ละตัวกับตัวแปรผลลัพธ์ สถิติ Durbin-Watson ไม่มีใน Excel อย่างไรก็ตาม ข้อมูลเป็นอิสระตามการออกแบบวิจัย (นักศึกษาต่างคนที่วัดครั้งเดียว) Histogram ของค่าคงเหลือแสดงการแจกแจงปกติโดยประมาณ และกราฟค่าคงเหลือบ่งชี้ความแปรปรวนคงที่ (homoscedasticity) ประเมิน Multicollinearity โดยใช้ correlation matrix ของตัวแปรทำนาย สหสัมพันธ์ส่วนใหญ่ต่ำ (r = 0.23–0.25) แม้ว่า Study_Hours และ Classes_Attended จะมีสหสัมพันธ์ที่อยู่ขอบเกณฑ์ (r = 0.82) ซึ่งเฝ้าดูแต่ไม่มีผลต่อความสามารถในการแปลผลค่าสัมประสิทธิ์อย่างมาก"

วิธีรายงานการถดถอยพหุคูณในรูปแบบ APA 7

คณะกรรมการวิทยานิพนธ์คาดหวังให้รายงานผลการถดถอยพหุคูณด้วยองค์ประกอบเฉพาะ นี่คือรูปแบบที่สมบูรณ์

แม่แบบส่วนผลการวิจัย APA

รูปแบบย่อหน้า:

"ดำเนินการวิเคราะห์การถดถอยเชิงเส้นพหุคูณเพื่อศึกษาว่าชั่วโมงการเรียน ชั่วโมงการนอน และการเข้าเรียน ทำนายคะแนนสอบปลายภาคหรือไม่ การวิเคราะห์เบื้องต้นยืนยันว่าข้อตกลงเบื้องต้นของความเป็นเส้นตรง ความเป็นอิสระ การแจกแจงปกติของค่าคงเหลือ ความแปรปรวนคงที่ และไม่มี multicollinearity ได้รับการตอบสนอง

โมเดลการถดถอยพหุคูณทำนายคะแนนสอบได้อย่างมีนัยสำคัญทางสถิติ, F(3, 26) = 373.65, p < .001, R² = .98, adjusted R² = .97 ตัวแปรทำนายสามตัวร่วมกันอธิบายความแปรปรวน 97.7% ของคะแนนสอบ ค่าสัมประสิทธิ์การถดถอยแสดงในตาราง [X]

ชั่วโมงการเรียนทำนายคะแนนสอบอย่างมีนัยสำคัญ (B = 1.75, 95% CI [1.46, 2.04], p < .001) เช่นเดียวกับการเข้าเรียน (B = 2.36, 95% CI [1.69, 3.04], p < .001) ชั่วโมงการนอนไม่ใช่ตัวทำนายที่มีนัยสำคัญทางสถิติ (B = 0.52, 95% CI [-0.09, 1.14], p = .092) สำหรับทุกชั่วโมงการเรียนรายสัปดาห์ที่เพิ่มขึ้น คะแนนสอบเพิ่มขึ้น 1.75 คะแนน เมื่อควบคุมการนอนและการเข้าเรียน ทุกคาบเรียนที่เข้าเพิ่มขึ้นสัมพันธ์กับคะแนนสอบที่เพิ่มขึ้น 2.36 คะแนน เมื่อควบคุมตัวแปรทำนายอื่น"

รูปแบบตาราง Regression แบบ APA

ตาราง [X]

การถดถอยเชิงเส้นพหุคูณทำนายคะแนนสอบ

ตัวแปร	B	SE	β	t	p	95% CI
Intercept	33.14	2.68	—	12.34	< .001	[27.63, 38.65]
ชั่วโมงการเรียน (Study_Hours)	1.75	0.14	1.04	12.50	< .001	[1.46, 2.04]
ชั่วโมงการนอน (Sleep_Hours)	0.52	0.30	.09	1.75	.092	[-0.09, 1.14]
การเข้าเรียน (Classes_Attended)	2.36	0.33	.63	7.22	< .001	[1.69, 3.04]

ตารางที่ 6: การถดถอยเชิงเส้นพหุคูณทำนายคะแนนสอบจากชั่วโมงการเรียน ชั่วโมงการนอน และการเข้าเรียน

หมายเหตุ. n = 30. R² = .98, adjusted R² = .97, F(3, 26) = 373.65, p < .001. B = ค่าสัมประสิทธิ์ไม่มาตรฐาน SE = ความคลาดเคลื่อนมาตรฐาน β = ค่าสัมประสิทธิ์มาตรฐาน CI = ช่วงความเชื่อมั่น

รายการตรวจสอบการรายงานการถดถอยพหุคูณ

รวมองค์ประกอบเหล่านี้ทั้งหมด:

ในเนื้อหา (ย่อหน้าผลการวิจัย):

ประเภทการวิเคราะห์ ("ดำเนินการวิเคราะห์การถดถอยเชิงเส้นพหุคูณ...")
ตัวแปรที่ทดสอบ (ตัวแปรทำนายทั้งหมดและตัวแปรผลลัพธ์)
ข้อความตรวจสอบข้อตกลงเบื้องต้น
นัยสำคัญของโมเดลโดยรวม: F(df_regression, df_residual) = ค่า F, p-value
R² และ R² ปรับแก้พร้อมการแปลผล
สำหรับตัวแปรทำนายแต่ละตัว: ค่า B, 95% CI และ p-value
ข้อความชัดเจนว่าตัวแปรทำนายใดมี/ไม่มีนัยสำคัญ
การแปลผลค่าสัมประสิทธิ์ที่มีนัยสำคัญพร้อมทิศทาง

ในตาราง:

หมายเลขตารางและหัวเรื่องเอียง
ตัวแปรทำนายทั้งหมดรวม intercept
B (ค่าสัมประสิทธิ์ไม่มาตรฐาน)
SE (ความคลาดเคลื่อนมาตรฐาน)
β (ค่าสัมประสิทธิ์มาตรฐาน) หากคำนวณ
สถิติ t
p-values
ช่วงความเชื่อมั่น 95%
หมายเหตุตารางพร้อม n, R², R² ปรับแก้, F-statistic

ข้อผิดพลาดทั่วไปในการถดถอยพหุคูณ

หลีกเลี่ยงข้อผิดพลาดที่พบบ่อยเหล่านี้ซึ่งอาจทำลายงานวิจัยวิทยานิพนธ์ของคุณ:

1. รายงาน R² แทน R² ปรับแก้

ข้อผิดพลาด: "โมเดลอธิบายความแปรปรวน 97.5% (R² = .975)"

ทำไมผิด: R² เพิ่มขึ้นเสมอเมื่อเพิ่มตัวแปรทำนาย แม้ตัวที่ไร้ประโยชน์ R² ปรับแก้แก้ไขสิ่งนี้

วิธีแก้ไข: รายงาน R² ปรับแก้เป็นขนาดผลหลัก หรือรายงานทั้งสอง: "R² = .972, adjusted R² = .969"

2. มองข้าม Multicollinearity

ข้อผิดพลาด: เพิ่มตัวแปรทำนายที่สัมพันธ์สูงโดยไม่ตรวจสอบ

ทำไมผิด: ค่าสัมประสิทธิ์ไม่เสถียร ความคลาดเคลื่อนมาตรฐานพอง และคุณไม่สามารถแปลผลว่าตัวแปรทำนายใดสำคัญ

วิธีแก้ไข: สร้าง correlation matrix ของตัวแปรทำนายเสมอก่อนทำ regression เอาออกหรือรวมตัวแปรที่มี r > 0.80

3. เอาตัวแปรทำนายที่ไม่มีนัยสำคัญออกโดยไม่มีเหตุผล

ข้อผิดพลาด: "การนอนไม่มีนัยสำคัญ ดังนั้นฉันเอามันออกและวิเคราะห์ใหม่"

ทำไมผิด: การเอาตัวแปรออกเปลี่ยนความหมายของค่าสัมประสิทธิ์อื่น การเอาออกแบบเลือกสรรอาจนำไปสู่ผลที่เบี่ยงเบน

วิธีแก้ไข: เก็บตัวแปรทำนายที่เกี่ยวข้องในทางทฤษฎีทั้งหมด รายงานตัวที่ไม่มีนัยสำคัญว่าไม่มีนัยสำคัญ เอาออกเฉพาะเมื่อมีเหตุผลทางทฤษฎีที่แข็งแกร่งและรายงานว่าคุณทำ

4. แปลผลค่าสัมประสิทธิ์ว่า "สำคัญที่สุด"

ข้อผิดพลาด: "ชั่วโมงการเรียน (B = 2.15) สำคัญกว่าการเข้าเรียน (B = 1.85) เพราะ 2.15 > 1.85"

ทำไมผิด: ค่าสัมประสิทธิ์ไม่มาตรฐานขึ้นอยู่กับมาตราวัดของแต่ละตัวแปร คุณกำลังเปรียบเทียบชั่วโมงกับคาบ - หน่วยต่างกัน

วิธีแก้ไข: คำนวณและเปรียบเทียบค่าสัมประสิทธิ์มาตรฐาน (β) สำหรับการเปรียบเทียบความสำคัญ

5. อ้างความเป็นเหตุเป็นผลจาก Regression

ข้อผิดพลาด: "การเรียนมากขึ้นทำให้คะแนนสอบสูงขึ้น"

ทำไมผิด: Regression แสดงการทำนายและความสัมพันธ์ ไม่ใช่สาเหตุ ความเป็นเหตุเป็นผลต้องการการออกแบบการทดลองที่มีการสุ่ม

วิธีแก้ไข: ใช้ภาษาระมัดระวัง - "ทำนาย" "สัมพันธ์กับ" "มีความเกี่ยวข้องกับ" แทน "ทำให้เกิด" "นำไปสู่" "ส่งผลให้"

6. ไม่ตรวจสอบข้อตกลงเบื้องต้น

ข้อผิดพลาด: ทำ regression โดยไม่ตรวจสอบความเป็นเส้นตรง การแจกแจงปกติ ความแปรปรวนคงที่ และ multicollinearity

ทำไมผิด: การละเมิดข้อตกลงเบื้องต้นนำไปสู่ค่าสัมประสิทธิ์ที่เบี่ยงเบนและ p-values ที่ไม่ถูกต้อง

วิธีแก้ไข: ตรวจสอบข้อตกลงเบื้องต้นทั้ง 5 ข้อเสมอก่อนสรุปผลลัพธ์ รายงานการตรวจสอบข้อตกลงเบื้องต้นใน Methods

7. ใช้ตัวแปรทำนายมากเกินไปสำหรับขนาดตัวอย่าง

ข้อผิดพลาด: ใส่ตัวแปรทำนาย 10 ตัวกับข้อมูลเพียง 50 ตัวอย่าง

ทำไมผิด: Overfitting เกิดขึ้นเมื่อโมเดลเหมาะกับตัวอย่างของคุณแต่ไม่สามารถ generalize ข้อกำหนดขั้นต่ำคือ n ≥ 50 + 8k

วิธีแก้ไข: ทำตามแนวทางขนาดตัวอย่าง สำหรับตัวแปรทำนาย 10 ตัว คุณต้องมีอย่างน้อย n = 130 ตัวอย่าง หากข้อมูลหายลดตัวอย่างที่ใช้ได้ จัดการสิ่งนี้ก่อน ดูวิธีจัดการข้อมูลที่หายไปสำหรับกลยุทธ์เพิ่มขนาดตัวอย่างที่ใช้ได้

สิ่งที่ Excel ทำไม่ได้: ข้อจำกัดสำหรับงานวิจัยวิทยานิพนธ์

Analysis ToolPak ของ Excel จัดการการถดถอยเชิงเส้นพหุคูณมาตรฐานได้ดี แต่มีข้อจำกัดสำคัญสำหรับเทคนิคขั้นสูง การเข้าใจสิ่งเหล่านี้ช่วยให้คุณเลือกซอฟต์แวร์ที่เหมาะสม

ประเภท Regression ที่ต้องใช้ SPSS หรือ R

เทคนิค	ทำอะไร	Excel?	ใช้แทน
Logistic Regression	ทำนายผลลัพธ์แบบสองทาง (ใช่/ไม่)	ไม่	SPSS, R
Stepwise Regression	เลือกตัวแปรอัตโนมัติ	ไม่	SPSS, R
Hierarchical Regression	เพิ่มตัวแปรทำนายเป็นบล็อก	ไม่	SPSS
Moderation Analysis	ทดสอบผลปฏิสัมพันธ์	ไม่	SPSS PROCESS
Mediation Analysis	ทดสอบผลทางอ้อม	ไม่	SPSS PROCESS
การคำนวณ VIF	ทดสอบ multicollinearity อย่างเป็นทางการ	ไม่	SPSS, R
Durbin-Watson	ทดสอบ autocorrelation	ไม่	SPSS, R
Polynomial Regression	ความสัมพันธ์โค้ง	ได้ (ทำมือ)	SPSS, R
Multiple Linear Regression	2+ ตัวแปรทำนายต่อเนื่อง	ได้	ซอฟต์แวร์ทั้งหมด

ตารางที่ 7: ความสามารถของ Excel ในการทำ Regression เทียบกับข้อกำหนดซอฟต์แวร์ทางสถิติ

เมื่อใดควรใช้ Excel vs SPSS/R

ใช้ Excel เมื่อ:

การถดถอยเชิงเส้นพหุคูณมาตรฐานเท่านั้น
ตัวแปรผลลัพธ์ต่อเนื่อง
ไม่ต้องการ VIF (correlation matrix เพียงพอ)
คณะกรรมการยอมรับผลลัพธ์จาก Excel
เรียนรู้ regression ก่อนวิธีขั้นสูง

ใช้ SPSS/R เมื่อ:

ผลลัพธ์แบบสองทาง/จัดกลุ่ม (logistic regression)
ต้องการ stepwise หรือ hierarchical regression
ทดสอบ moderation หรือ mediation
คณะกรรมการต้องการ VIF, Durbin-Watson
ตีพิมพ์ในวารสารที่ต้องการผลลัพธ์จาก SPSS/R

สรุปสำคัญ: Excel ดีเยี่ยมสำหรับเรียนรู้การถดถอยพหุคูณและสำหรับการวิเคราะห์วิทยานิพนธ์พื้นฐาน สำหรับเทคนิคขั้นสูงหรือการทดสอบ multicollinearity อย่างเป็นทางการ คุณจะต้องใช้ SPSS หรือ R ตรวจสอบกับอาจารย์ที่ปรึกษาเกี่ยวกับข้อกำหนดซอฟต์แวร์

คำถามที่พบบ่อย

คำถามจากคณะกรรมการที่คุณควรเตรียมตอบ

คณะกรรมการวิทยานิพนธ์มักถามคำถามเหล่านี้เกี่ยวกับการวิเคราะห์การถดถอยพหุคูณ การเตรียมคำตอบล่วงหน้าแสดงความสามารถทางสถิติและเสริมความแข็งแกร่งในการสอบ

"ทำไมคุณรวมตัวแปรทำนายเหล่านี้โดยเฉพาะ?"

เตรียมให้เหตุผลแต่ละตัวแปรตามทฤษฎีและงานวิจัยก่อนหน้า ไม่ใช่เพียงความสะดวกทางสถิติ อ้างอิงเอกสารที่แสดงว่าทำไมตัวแปรทำนายแต่ละตัวควรมีความเกี่ยวข้องกับผลลัพธ์อย่างมีเหตุผล คณะกรรมการสงสัย "data dredging" ที่ตัวแปรทำนายรวมเข้ามาเพียงเพราะมีข้อมูลอยู่

"คุณตรวจสอบ multicollinearity หรือไม่?"

แสดง correlation matrix และอธิบายว่าสหสัมพันธ์ของตัวแปรทำนายทั้งหมดต่ำกว่า 0.80 (หรือเกณฑ์ที่คุณใช้) หากถูกถามเกี่ยวกับ VIF และคุณใช้ Excel อธิบายว่าแม้ Excel ไม่สามารถคำนวณ VIF โดยตรง วิธี correlation matrix ระบุ multicollinearity ที่เป็นปัญหาได้ ยอมรับว่า SPSS หรือ R จำเป็นสำหรับการทดสอบ VIF อย่างเป็นทางการ

"ทำไม [ตัวแปร] ไม่มีนัยสำคัญ?"

ตัวแปรทำนายที่ไม่มีนัยสำคัญไม่ได้หมายความว่าตัวแปรนั้นไม่สำคัญ อธิบายว่าเมื่อควบคุมตัวแปรทำนายอื่น การมีส่วนร่วมเฉพาะของตัวแปรนี้ไม่สามารถแยกแยะจากศูนย์ได้ทางสถิติ เหตุผลที่เป็นไปได้รวมถึง: ทับซ้อนกับตัวแปรทำนายอื่น (ความแปรปรวนร่วม) ขนาดตัวอย่างไม่เพียงพอที่จะตรวจพบผลขนาดเล็ก หรือไม่มีความสัมพันธ์เฉพาะจริงๆ หลังจากควบคุมตัวแปรกวน

"ความสำคัญในทางปฏิบัติของผลลัพธ์เหล่านี้คืออะไร?"

นัยสำคัญทางสถิติไม่เหมือนกับความสำคัญในทางปฏิบัติ เตรียมอธิบายว่าค่าสัมประสิทธิ์หมายความว่าอะไรในแง่จริง ตัวอย่าง: "ทุกชั่วโมงการเรียนที่เพิ่มขึ้นสัมพันธ์กับคะแนนสอบเพิ่มขึ้น 1.75 คะแนน ตลอดภาคการศึกษา นักศึกษาที่เรียนมากกว่าค่าเฉลี่ย 10 ชั่วโมงต่อสัปดาห์อาจคาดหวังคะแนนเพิ่มประมาณ 17.5 คะแนน อาจเป็นความแตกต่างระหว่างเกรด B กับ A"

"ทำไมคุณไม่ใช้ SPSS หรือ R?"

หากถูกถาม อธิบายว่า Analysis ToolPak ของ Excel จัดการการถดถอยเชิงเส้นพหุคูณมาตรฐานได้เพียงพอสำหรับการออกแบบวิจัยของคุณ ยอมรับข้อจำกัดของ Excel (ไม่มี VIF ไม่มี stepwise regression ไม่มี logistic regression) และอธิบายว่าทำไมสิ่งเหล่านี้ไม่จำเป็นสำหรับการวิเคราะห์เฉพาะของคุณ หากคณะกรรมการต้องการผลลัพธ์จาก SPSS เป็นพิเศษ เสนอที่จะทำการวิเคราะห์ซ้ำใน SPSS สำหรับการส่งงานครั้งสุดท้าย

ขั้นตอนถัดไป: การประยุกต์ใช้การถดถอยพหุคูณกับวิทยานิพนธ์ของคุณ

ตอนนี้คุณมีกรอบการทำงานที่สมบูรณ์สำหรับการวิเคราะห์การถดถอยเชิงเส้นพหุคูณใน Excel - ตั้งแต่เข้าใจว่าเมื่อใดควรใช้ ผ่านการทำการวิเคราะห์ ไปจนถึงแปลผลและรายงานในรูปแบบ APA กุญแจสู่ความสำเร็จไม่ใช่แค่การทำการวิเคราะห์ แต่เข้าใจว่าผลลัพธ์แต่ละตัวหมายความว่าอะไรและตรวจสอบว่าข้อมูลของคุณตรงตามข้อตกลงเบื้องต้น

ก่อนสรุปการวิเคราะห์:

ตรวจสอบ multicollinearity ก่อน - สร้าง correlation matrix ของตัวแปรทำนายก่อนทำ regression สหสัมพันธ์ > 0.80 ต้องจัดการ
ตรวจสอบข้อตกลงเบื้องต้นทั้ง 5 ข้อ - ความเป็นเส้นตรง ความเป็นอิสระ การแจกแจงปกติของค่าคงเหลือ ความแปรปรวนคงที่ และไม่มี multicollinearity
ใช้ R² ปรับแก้ - นี่คือขนาดผลที่เหมาะสมสำหรับการถดถอยพหุคูณ ไม่ใช่ R² ปกติ
รายงานตัวแปรทำนายทั้งหมด - รวมตัวแปรทำนายที่ไม่มีนัยสำคัญในตารางผลการวิจัย อย่าเอาตัวแปรออกแบบเลือกสรรโดยไม่มีเหตุผลที่แข็งแกร่ง
รู้ข้อจำกัดของ Excel - หากคุณต้องการ VIF, stepwise regression หรือ logistic regression คุณจะต้องใช้ SPSS หรือ R

คู่มือที่เกี่ยวข้องเพื่อเรียนรู้ต่อ:

ความรู้พื้นฐาน: การถดถอยเชิงเส้นอย่างง่ายใน Excel - ทบทวนหากแนวคิดที่นี่ไม่ชัดเจน
สหสัมพันธ์: ค่าสหสัมพันธ์ Pearson - สำหรับตรวจสอบ multicollinearity
ขนาดผล: วิธีคำนวณ Effect Size - สำหรับแปลผลความสำคัญในทางปฏิบัติ
การรายงาน: รายงานสถิติเชิงพรรณนาใน APA - สำหรับบทผลการวิจัยที่สมบูรณ์
ความแตกต่างของกลุ่ม: ANOVA ใน Excel - เมื่อตัวแปรทำนายเป็นกลุ่มจัดประเภท

เอกสารอ้างอิง

American Psychological Association. (2020). Publication manual of the American Psychological Association (7th ed.). https://doi.org/10.1037/0000165-000

Cohen, J. (1988). Statistical power analysis for the behavioral sciences (2nd ed.). Lawrence Erlbaum Associates.

Green, S. B. (1991). How many subjects does it take to do a regression analysis? Multivariate Behavioral Research, 26(3), 499–510. https://doi.org/10.1207/s15327906mbr2603_7

Hair, J. F., Black, W. C., Babin, B. J., & Anderson, R. E. (2019). Multivariate data analysis (8th ed.). Cengage Learning.

Tabachnick, B. G., & Fidell, L. S. (2019). Using multivariate statistics (7th ed.). Pearson.