Simple linear regression คืออะไร และควรใช้เมื่อไหร่สำหรับวิทยานิพนธ์

Simple linear regression (การถดถอยเชิงเส้นอย่างง่าย) ก็คือการทำนายค่าของตัวแปรตาม (Y) จากตัวแปรอิสระตัวเดียว (X) คุณควรใช้วิธีนี้เมื่ออยากรู้ว่าตัวแปรหนึ่งสามารถทำนายอีกตัวแปรหนึ่งได้แค่ไหน เช่น 'เวลาที่ใช้อ่านหนังสือทำนายคะแนนสอบได้ไหม' หรือ 'งบโฆษณาทำนายยอดขายได้ไหม' สำหรับงานวิจัยวิทยานิพนธ์ simple linear regression เหมาะกับงานที่มีตัวแปรทำนาย (predictor) ตัวเดียวและตัวแปรผล (outcome) ตัวเดียวที่เป็นข้อมูลต่อเนื่อง และคำถามวิจัยของคุณมุ่งเน้นที่การทำนายหรือการวัดความแข็งแรงของความสัมพันธ์เชิงเส้น

ความแตกต่างระหว่าง simple linear regression กับ correlation คืออะไร

Correlation (สหสัมพันธ์) วัดความแข็งแรงและทิศทางของความสัมพันธ์ระหว่างตัวแปรสองตัว (ค่าอยู่ระหว่าง -1 ถึง +1) ในขณะที่ regression ทำนายค่า Y และบอกว่า Y เปลี่ยนแปลงเท่าไหร่เมื่อ X เพิ่มขึ้นหนึ่งหน่วย Correlation ถือว่า X และ Y เท่าเทียมกัน แต่ regression แยกว่าตัวไหนเป็นตัวทำนาย (X) และตัวไหนเป็นผล (Y) ใช้ correlation เมื่อแค่อยากรู้ว่าตัวแปรสัมพันธ์กันหรือเปล่า ใช้ regression เมื่ออยากทำนายค่า เข้าใจทิศทางของอิทธิพล หรือรายงานว่าตัวแปรหนึ่งมีผลต่ออีกตัวแปรหนึ่งเท่าไหร่ในบทที่ 4 (ผลการวิจัย) ของวิทยานิพนธ์

ตีความ R-squared ใน simple linear regression อย่างไร

R-squared (R²) แสดงเปอร์เซ็นต์ของความแปรปรวนในตัวแปรตามที่อธิบายได้ด้วยตัวแปรอิสระ ตัวอย่าง R² = 0.64 หมายความว่า 64% ของความแปรปรวนในคะแนนสอบอธิบายได้ด้วยชั่วโมงการอ่านหนังสือ ส่วนอีก 36% เกิดจากปัจจัยอื่น ตาม Cohen (1988) สำหรับวิทยาศาสตร์พฤติกรรม r² = .01 ถือว่าเล็ก r² = .09 ถือว่าปานกลาง และ r² = .25 ถือว่าใหญ่ แต่มาตรฐานเหล่านี้แตกต่างกันมากในแต่ละสาขา สิ่งที่ถือว่า 'อ่อน' ในฟิสิกส์ (R² < 0.90) อาจถือว่า 'ใหญ่' ในจิตวิทยา ควรตีความ R² ตามมาตรฐานของสาขาวิชาของคุณเสมอ และรายงาน R² ในส่วนผลการวิจัยเป็นตัววัดขนาดอิทธิพล (effect size) แม้ค่า p-value จะมีนัยสำคัญก็ตาม

ค่า p-value ในผล regression หมายความว่าอย่างไร และควรรายงานอะไรบ้าง

ค่า p-value ของ Significance F ทดสอบว่าโมเดล regression โดยรวมมีนัยสำคัญทางสถิติหรือไม่ (X เป็นตัวทำนาย Y ที่มีประโยชน์ไหม) ถ้า p < 0.05 โมเดลมีนัยสำคัญ ส่วนค่า p-value ของ coefficient แต่ละตัวทดสอบว่าตัวทำนายแต่ละตัวแตกต่างจากศูนย์อย่างมีนัยสำคัญหรือไม่ สำหรับ simple linear regression คุณจะมี p-value สองค่า หนึ่งสำหรับ intercept (มักไม่สำคัญ) และอีกหนึ่งสำหรับตัวแปรทำนายของคุณ (สำคัญมากสำหรับข้อสรุป) ควรรายงานทั้ง Significance F และ coefficient p-value ในบทที่ 4 (ผลการวิจัย) ของวิทยานิพนธ์

เช็คว่าข้อมูลเข้าสมมติฐานสำหรับ linear regression ใน Excel อย่างไร

เช็คสมมติฐานสำคัญสี่ข้อใน Excel (1) ความเป็นเส้นตรง (Linearity): สร้าง scatter plot ของ X vs Y ความสัมพันธ์ควรเป็นเส้นตรงโดยประมาณ ไม่โค้ง (2) ความเป็นอิสระ (Independence): ตรวจสอบให้แน่ใจว่าข้อมูลแต่ละตัวเป็นอิสระต่อกัน (ไม่มีการวัดซ้ำ) (3) การแจกแจงปกติของ residuals (Normality): สร้างฮิสโตแกรมของ residuals จากผล regression ควรมีรูปร่างคล้ายระฆัง (4) ความแปรปรวนคงที่ (Homoscedasticity): พล็อต residuals vs fitted values การกระจายควรค่อนข้างคงที่ตลอดช่วงค่า X ถ้าละเมิดสมมติฐาน ผล regression อาจไม่น่าเชื่อถือ ลองพิจารณาแปลงตัวแปร (transform) หรือใช้วิธีที่ไม่ใช้พารามิเตอร์ (non-parametric alternatives)

รายงานผล simple linear regression ตามรูปแบบ APA 7th edition อย่างไร

รายงาน regression ตามลำดับนี้ (1) ระบุการวิเคราะห์ที่ใช้: 'ทำการวิเคราะห์ simple linear regression เพื่อทำนาย...' (2) รายงานความเหมาะสมของโมเดล: 'โมเดล regression มีนัยสำคัญทางสถิติ F(1, 28) = 850.27, p < .001, R² = .97' (3) รายงานสมการ: 'สมการ regression คือ Exam Score = 47.33 + 2.75(Study Hours)' (4) ตีความค่า coefficient: 'ทุกๆ ชั่วโมงเพิ่มเติมของการอ่านหนังสือ คะแนนสอบเพิ่มขึ้นเฉลี่ย 2.75 คะแนน (95% CI [2.56, 2.95])' รวมถึงตารางแสดงค่า unstandardized coefficients, standard errors, t-values และ p-values ด้วย

Excel ทำ regression แบบไหนไม่ได้บ้างที่ต้องรู้

Excel ทำไม่ได้: (1) Logistic regression (สำหรับผลลัพธ์แบบไบนารี เช่น ผ่าน/ไม่ผ่าน) ใช้ SPSS หรือ R (2) Stepwise regression (การเลือกตัวแปรอัตโนมัติ) ใช้ SPSS หรือ R (3) Hierarchical regression (การเพิ่มตัวทำนายเป็นบล็อก) ใช้ SPSS (4) การวิเคราะห์ moderation หรือ mediation (PROCESS macro) ใช้ SPSS กับ PROCESS (5) การวินิจฉัยขั้นสูง (VIF สำหรับ multicollinearity, Durbin-Watson สำหรับ autocorrelation) ใช้ SPSS หรือ R ถ้าคณะกรรมการวิทยานิพนธ์ของคุณต้องการเทคนิคเหล่านี้ คุณจะต้องใช้โปรแกรมสถิตินอกเหนือจาก Excel Excel เหมาะสำหรับ simple linear regression และ multiple linear regression เท่านั้น

ใช้ simple linear regression ได้ไหมถ้าตัวแปรตามเป็นข้อมูลเชิงกลุ่ม

ไม่ได้นะ simple linear regression ต้องการตัวแปรตามที่เป็นข้อมูลต่อเนื่อง (interval หรือ ratio scale) ถ้าตัวแปรตามของคุณเป็นข้อมูลเชิงกลุ่ม (ใช่/ไม่ใช่, ผ่าน/ไม่ผ่าน, ต่ำ/กลาง/สูง) คุณใช้ linear regression ใน Excel ไม่ได้ สำหรับผลลัพธ์แบบไบนารี (สองกลุ่ม) ใช้ logistic regression ใน SPSS หรือ R สำหรับผลลัพธ์แบบ ordinal (กลุ่มที่มีลำดับ) ใช้ ordinal regression สำหรับผลลัพธ์แบบ nominal (กลุ่มที่ไม่มีลำดับ) ใช้ multinomial logistic regression Linear regression สมมติว่าตัวแปร Y ของคุณสามารถมีค่าใดก็ได้ในระดับต่อเนื่อง ไม่ใช่กลุ่มแยกส่วน

ขนาดตัวอย่างที่ดีสำหรับ simple linear regression ในงานวิจัยวิทยานิพนธ์คือเท่าไหร่

สำหรับ simple linear regression ต้องการข้อมูลอย่างน้อย n = 30 ตัวอย่างสำหรับการวิเคราะห์พื้นฐาน แต่แนะนำ n = 50-100 สำหรับงานวิจัยวิทยานิพนธ์เพื่อให้แน่ใจว่ามี statistical power เพียงพอและค่าประมาณ coefficient มีเสถียรภาพ ตาม Green (1991) ต้องการ n ≥ 104 + k เพื่อทดสอบโมเดลโดยรวม (โดยที่ k = จำนวนตัวทำนาย) และ n ≥ 50 + 8k เพื่อทดสอบตัวทำนายแต่ละตัว สำหรับ simple regression ที่มีตัวทำนายหนึ่งตัว แนะนำ n ≥ 105 สำหรับการวิเคราะห์ที่เข้มงวด แต่วิธีที่น่าเชื่อถือที่สุดคือทำ a priori power analysis ด้วยโปรแกรมอย่าง G*Power ก่อนเก็บข้อมูล วิธีนี้จะช่วยให้คุณกำหนดขนาดตัวอย่างที่ต้องการได้อย่างแม่นยำโดยอิงจาก expected effect size, desired power (ปกติ .80) และ alpha level (.05)

สร้าง scatter plot พร้อมเส้น regression ใน Excel อย่างไร

เลือกข้อมูล X และ Y (รวมหัวคอลัมน์) ไปที่ Insert → Charts → Scatter → Scatter with only Markers คลิกที่จุดข้อมูลใดก็ได้ คลิกขวา เลือก Add Trendline ใน Trendline Options เลือก 'Display Equation on chart' และ 'Display R-squared value on chart' เลือกประเภท Linear trendline จัดรูปแบบ trendline ด้วยเส้นทึบและสีที่เหมาะสม เพิ่มชื่อแกน (axis titles) ที่บอกว่าตัวแปรของคุณคืออะไร กราฟนี้สำคัญมากสำหรับวิทยานิพนธ์เพื่อแสดงความสัมพันธ์เชิงเส้นก่อนรายงานผลเป็นตัวเลข

ควรทำอย่างไรถ้าสมมติฐาน regression ถูกละเมิด

ถ้าสมมติฐานความเป็นเส้นตรงถูกละเมิด (รูปแบบโค้งใน scatter plot) ลองแปลงตัวแปร X หรือ Y (log, square root, หรือ square transformations) ถ้าสมมติฐานการแจกแจงปกติของ residuals ถูกละเมิด (ฮิสโตแกรมเบ้) เช็ค outliers หรือแปลงตัวแปร Y ถ้าสมมติฐาน homoscedasticity ถูกละเมิด (รูปแบบกรวยใน residual plot) พิจารณา weighted least squares หรือแปลงตัวแปร Y ถ้าสมมติฐานความเป็นอิสระถูกละเมิด (repeated measures) ใช้ mixed-effects models แทน สำหรับงานวิจัยวิทยานิพนธ์ ควรรายงานการเช็คสมมติฐานในบทที่ 3 (ระเบียบวิธีวิจัย) เสมอ และยอมรับการละเมิดเป็นข้อจำกัดถ้าการแปลงตัวแปรไม่ช่วย ปรึกษาอาจารย์ที่ปรึกษาถ้าการละเมิดรุนแรง

วิธีคำนวณการถดถอยเชิงเส้นอย่างง่าย (Simple Linear Regression) ใน Excel สำหรับวิทยานิพนธ์

Q: ค่า p-value ในผล regression หมายความว่าอย่างไร และควรรายงานอะไรบ้าง

ค่า p-value ของ Significance F ทดสอบว่าโมเดล regression โดยรวมมีนัยสำคัญทางสถิติหรือไม่ (X เป็นตัวทำนาย Y ที่มีประโยชน์ไหม) ถ้า p < 0.05 โมเดลมีนัยสำคัญ ส่วนค่า p-value ของ coefficient แต่ละตัวทดสอบว่าตัวทำนายแต่ละตัวแตกต่างจากศูนย์อย่างมีนัยสำคัญหรือไม่ สำหรับ simple linear regression คุณจะมี p-value สองค่า หนึ่งสำหรับ intercept (มักไม่สำคัญ) และอีกหนึ่งสำหรับตัวแปรทำนายของคุณ (สำคัญมากสำหรับข้อสรุป) ควรรายงานทั้ง Significance F และ coefficient p-value ในบทที่ 4 (ผลการวิจัย) ของวิทยานิพนธ์

Q: เช็คว่าข้อมูลเข้าสมมติฐานสำหรับ linear regression ใน Excel อย่างไร

เช็คสมมติฐานสำคัญสี่ข้อใน Excel (1) ความเป็นเส้นตรง (Linearity): สร้าง scatter plot ของ X vs Y ความสัมพันธ์ควรเป็นเส้นตรงโดยประมาณ ไม่โค้ง (2) ความเป็นอิสระ (Independence): ตรวจสอบให้แน่ใจว่าข้อมูลแต่ละตัวเป็นอิสระต่อกัน (ไม่มีการวัดซ้ำ) (3) การแจกแจงปกติของ residuals (Normality): สร้างฮิสโตแกรมของ residuals จากผล regression ควรมีรูปร่างคล้ายระฆัง (4) ความแปรปรวนคงที่ (Homoscedasticity): พล็อต residuals vs fitted values การกระจายควรค่อนข้างคงที่ตลอดช่วงค่า X ถ้าละเมิดสมมติฐาน ผล regression อาจไม่น่าเชื่อถือ ลองพิจารณาแปลงตัวแปร (transform) หรือใช้วิธีที่ไม่ใช้พารามิเตอร์ (non-parametric alternatives)

Q: รายงานผล simple linear regression ตามรูปแบบ APA 7th edition อย่างไร

รายงาน regression ตามลำดับนี้ (1) ระบุการวิเคราะห์ที่ใช้: 'ทำการวิเคราะห์ simple linear regression เพื่อทำนาย...' (2) รายงานความเหมาะสมของโมเดล: 'โมเดล regression มีนัยสำคัญทางสถิติ F(1, 28) = 850.27, p < .001, R² = .97' (3) รายงานสมการ: 'สมการ regression คือ Exam Score = 47.33 + 2.75(Study Hours)' (4) ตีความค่า coefficient: 'ทุกๆ ชั่วโมงเพิ่มเติมของการอ่านหนังสือ คะแนนสอบเพิ่มขึ้นเฉลี่ย 2.75 คะแนน (95% CI [2.56, 2.95])' รวมถึงตารางแสดงค่า unstandardized coefficients, standard errors, t-values และ p-values ด้วย

Q: Excel ทำ regression แบบไหนไม่ได้บ้างที่ต้องรู้

Excel ทำไม่ได้: (1) Logistic regression (สำหรับผลลัพธ์แบบไบนารี เช่น ผ่าน/ไม่ผ่าน) ใช้ SPSS หรือ R (2) Stepwise regression (การเลือกตัวแปรอัตโนมัติ) ใช้ SPSS หรือ R (3) Hierarchical regression (การเพิ่มตัวทำนายเป็นบล็อก) ใช้ SPSS (4) การวิเคราะห์ moderation หรือ mediation (PROCESS macro) ใช้ SPSS กับ PROCESS (5) การวินิจฉัยขั้นสูง (VIF สำหรับ multicollinearity, Durbin-Watson สำหรับ autocorrelation) ใช้ SPSS หรือ R ถ้าคณะกรรมการวิทยานิพนธ์ของคุณต้องการเทคนิคเหล่านี้ คุณจะต้องใช้โปรแกรมสถิตินอกเหนือจาก Excel Excel เหมาะสำหรับ simple linear regression และ multiple linear regression เท่านั้น

Q: ใช้ simple linear regression ได้ไหมถ้าตัวแปรตามเป็นข้อมูลเชิงกลุ่ม

ไม่ได้นะ simple linear regression ต้องการตัวแปรตามที่เป็นข้อมูลต่อเนื่อง (interval หรือ ratio scale) ถ้าตัวแปรตามของคุณเป็นข้อมูลเชิงกลุ่ม (ใช่/ไม่ใช่, ผ่าน/ไม่ผ่าน, ต่ำ/กลาง/สูง) คุณใช้ linear regression ใน Excel ไม่ได้ สำหรับผลลัพธ์แบบไบนารี (สองกลุ่ม) ใช้ logistic regression ใน SPSS หรือ R สำหรับผลลัพธ์แบบ ordinal (กลุ่มที่มีลำดับ) ใช้ ordinal regression สำหรับผลลัพธ์แบบ nominal (กลุ่มที่ไม่มีลำดับ) ใช้ multinomial logistic regression Linear regression สมมติว่าตัวแปร Y ของคุณสามารถมีค่าใดก็ได้ในระดับต่อเนื่อง ไม่ใช่กลุ่มแยกส่วน

Q: ขนาดตัวอย่างที่ดีสำหรับ simple linear regression ในงานวิจัยวิทยานิพนธ์คือเท่าไหร่

สำหรับ simple linear regression ต้องการข้อมูลอย่างน้อย n = 30 ตัวอย่างสำหรับการวิเคราะห์พื้นฐาน แต่แนะนำ n = 50-100 สำหรับงานวิจัยวิทยานิพนธ์เพื่อให้แน่ใจว่ามี statistical power เพียงพอและค่าประมาณ coefficient มีเสถียรภาพ ตาม Green (1991) ต้องการ n ≥ 104 + k เพื่อทดสอบโมเดลโดยรวม (โดยที่ k = จำนวนตัวทำนาย) และ n ≥ 50 + 8k เพื่อทดสอบตัวทำนายแต่ละตัว สำหรับ simple regression ที่มีตัวทำนายหนึ่งตัว แนะนำ n ≥ 105 สำหรับการวิเคราะห์ที่เข้มงวด แต่วิธีที่น่าเชื่อถือที่สุดคือทำ a priori power analysis ด้วยโปรแกรมอย่าง G*Power ก่อนเก็บข้อมูล วิธีนี้จะช่วยให้คุณกำหนดขนาดตัวอย่างที่ต้องการได้อย่างแม่นยำโดยอิงจาก expected effect size, desired power (ปกติ .80) และ alpha level (.05)

Q: สร้าง scatter plot พร้อมเส้น regression ใน Excel อย่างไร

เลือกข้อมูล X และ Y (รวมหัวคอลัมน์) ไปที่ Insert → Charts → Scatter → Scatter with only Markers คลิกที่จุดข้อมูลใดก็ได้ คลิกขวา เลือก Add Trendline ใน Trendline Options เลือก 'Display Equation on chart' และ 'Display R-squared value on chart' เลือกประเภท Linear trendline จัดรูปแบบ trendline ด้วยเส้นทึบและสีที่เหมาะสม เพิ่มชื่อแกน (axis titles) ที่บอกว่าตัวแปรของคุณคืออะไร กราฟนี้สำคัญมากสำหรับวิทยานิพนธ์เพื่อแสดงความสัมพันธ์เชิงเส้นก่อนรายงานผลเป็นตัวเลข

การถดถอยเชิงเส้นอย่างง่าย (simple linear regression) เป็นหนึ่งในเทคนิคทางสถิติที่ทรงพลังแต่เข้าถึงได้ง่ายที่สุดสำหรับงานวิจัยวิทยานิพนธ์ ไม่ว่าคุณจะทำนายผลการเรียนของนักเรียนจากชั่วโมงการอ่านหนังสือ ยอดขายจากงบโฆษณา หรือผลลัพธ์ของผู้ป่วยจากระยะเวลาการรักษา simple linear regression จะช่วยให้คุณวัดความสัมพันธ์และทำการทำนายตามหลักฐานเชิงประจักษ์โดยใช้ Analysis ToolPak ที่มีใน Excel

ต่างจากการวิเคราะห์สหสัมพันธ์ (correlation) ที่บอกแค่ว่าตัวแปรสัมพันธ์กันหรือเปล่า regression ช่วยให้คุณทำนายค่าเฉพาะ เข้าใจทิศทางของอิทธิพล และวัดได้อย่างแม่นยำว่าตัวแปรผลของคุณเปลี่ยนแปลงเท่าไหร่เมื่อตัวแปรทำนายเพิ่มขึ้นหนึ่งหน่วย นี่ทำให้ regression เป็นเครื่องมือสำคัญสำหรับบทที่ 4 (ผลการวิจัย) ในวิทยานิพนธ์ทั่วทุกสาขา ไม่ว่าจะเป็นจิตวิทยา การศึกษา ธุรกิจ วิทยาศาสตร์สุขภาพ และสังคมศาสตร์

คู่มือฉบับละเอียดนี้จะแสดงให้คุณเห็นวิธีคำนวณ simple linear regression ใน Excel ด้วยสามวิธี เช็คสมมติฐานทั้งสี่ข้อ ตีความผลอย่างถูกต้อง และรายงานผลตามรูปแบบ APA 7th edition คุณจะได้เรียนรู้ข้อจำกัดสำคัญของ Excel regression และเมื่อไหร่ที่คุณต้องใช้ SPSS หรือ R แทน

คุณจะได้เรียนรู้:

Simple linear regression คืออะไร และใช้เมื่อไหร่สำหรับงานวิจัยวิทยานิพนธ์
วิธีคำนวณ regression ด้วย Analysis ToolPak (แนะนำ), scatter plot trendlines และฟังก์ชัน LINEST
วิธีตีความ R-squared, p-values, coefficients และ standard errors
วิธีเช็คสมมติฐาน (linearity, normality, homoscedasticity) ใน Excel
วิธีรายงานผล ตามรูปแบบ APA 7th edition สำหรับวิทยานิพนธ์
ข้อจำกัดของ Excel และ regression ประเภทไหนต้องใช้ SPSS/R

เทคนิคเหล่านี้ใช้ได้ไม่ว่าคุณจะวิเคราะห์ข้อมูลจากการทดลอง คำตอบจากแบบสอบถาม หรือข้อมูลจากการสังเกตที่มีตัวแปรต่อเนื่อง

ก่อนเริ่ม: คู่มือนี้สมมติว่าคุณมี Excel พร้อม Analysis ToolPak ติดตั้งแล้ว ถ้ายังไม่ได้เปิดใช้งาน ดูคู่มือของเราเรื่อง วิธีเพิ่ม Data Analysis ใน Excel คุณควรคุ้นเคยกับสถิติเชิงพรรณนาพื้นฐาน และเข้าใจตัวแปรอิสระและตัวแปรตาม ด้วย

Simple Linear Regression คืออะไร

Simple linear regression (การถดถอยเชิงเส้นอย่างง่าย) ก็คือวิธีทางสถิติที่ใช้สร้างโมเดลความสัมพันธ์ระหว่างตัวแปรอิสระตัวเดียว (ตัวทำนาย, X) กับตัวแปรตามตัวเดียว (ผลลัพธ์, Y) โดยการลากเส้นตรงผ่านจุดข้อมูลของคุณ เส้น regression นี้แสดงถึงการทำนาย Y ที่ดีที่สุดจาก X โดยลดผลรวมของผลต่างกำลังสองระหว่างค่าที่สังเกตได้และค่าที่ทำนายให้น้อยที่สุด เราเรียกวิธีนี้ว่า least squares method

สมการ Regression

สมการ simple linear regression คือ

$Y = a + bX + \varepsilon$

โดยที่

Y = ตัวแปรตาม (สิ่งที่คุณกำลังทำนาย)
X = ตัวแปรอิสระ (ตัวทำนายของคุณ)
a = Intercept (ค่า Y ที่คาดหวังเมื่อ X = 0)
b = Slope coefficient (การเปลี่ยนแปลงของ Y เมื่อ X เพิ่มขึ้น 1 หน่วย)
ε = Error term (ความแปรปรวนที่อธิบายไม่ได้)

ตัวอย่าง ถ้าคุณทำนายคะแนนสอบจากชั่วโมงการอ่านหนังสือ

$\text{คะแนนสอบ} = 47.33 + 2.75 \times \text{ชั่วโมงอ่านหนังสือ}$

นี่หมายความว่า นักเรียนที่ไม่อ่านหนังสือเลย (0 ชั่วโมง) คาดว่าจะได้ 47.33 คะแนน และทุกๆ ชั่วโมงเพิ่มเติมของการอ่านหนังสือจะเพิ่มคะแนนเฉลี่ย 2.75 คะแนน

เมื่อไหร่ควรใช้ Simple Linear Regression สำหรับวิทยานิพนธ์

ใช้ simple linear regression เมื่องานวิจัยของคุณตรงตามเกณฑ์เหล่านี้

1. ข้อกำหนดของคำถามวิจัย:

คุณอยากทำนายค่า Y จาก X
คุณอยากวัดว่า Y เปลี่ยนแปลงเท่าไหร่เมื่อ X เพิ่มขึ้น
คุณอยากทดสอบว่า X เป็นตัวทำนายที่มีนัยสำคัญของ Y หรือไม่

2. ข้อกำหนดของตัวแปร:

ตัวทำนายต่อเนื่องหนึ่งตัว (X): ระดับ interval หรือ ratio (เช่น อายุ รายได้ คะแนนสอบ เวลา)
ตัวแปรผลต่อเนื่องหนึ่งตัว (Y): ระดับ interval หรือ ratio
ทั้งสองตัวแปรควรมีจุดข้อมูลอย่างน้อย 30 จุด

3. ตัวอย่างงานวิจัยในแต่ละสาขา:

จิตวิทยา: จำนวนครั้งของการบำบัดทำนายการลดลงของอาการซึมเศร้าได้ไหม
การศึกษา: การเข้าเรียนทำนายคะแนนสอบปลายภาคได้ไหม
ธุรกิจ: งบโฆษณาทำนายยอดขายรายเดือนได้ไหม
วิทยาศาสตร์สุขภาพ: จำนวนนาทีการออกกำลังกายต่อสัปดาห์ทำนายการลดน้ำหนักได้ไหม
สังคมศาสตร์: ระดับรายได้ทำนายคะแนนความพึงพอใจในชีวิตได้ไหม

Simple Linear Regression vs Correlation

นักศึกษาหลายคนมักสับสน regression กับ correlation นี่คือความแตกต่างสำคัญ

ด้าน	Correlation (สหสัมพันธ์)	Simple Linear Regression
วัตถุประสงค์	วัดความแข็งแรงและทิศทางของความสัมพันธ์	ทำนาย Y จาก X และวัดขนาดอิทธิพล
ผลลัพธ์	ค่าสัมประสิทธิ์สหสัมพันธ์ (r) ตั้งแต่ -1 ถึง +1	สมการ regression (Y = a + bX)
ตัวแปร	ถือว่า X และ Y เท่าเทียมกัน (symmetric)	แยกตัวทำนาย (X) จากผลลัพธ์ (Y)
การตีความ	"X และ Y สัมพันธ์กัน"	"X เพิ่มขึ้นหนึ่งหน่วย Y เปลี่ยนแปลง b หน่วย"
ใช้ในวิทยานิพนธ์	การวิเคราะห์เบื้องต้น สำรวจความสัมพันธ์	การวิเคราะห์หลักสำหรับการทำนายและวัดอิทธิพล
ตัวอย่าง	ชั่วโมงอ่านหนังสือและคะแนนสอบมีความสัมพันธ์ทางบวก (r = 0.98)	ทุกๆ ชั่วโมงเพิ่มเติมของการอ่านหนังสือเพิ่มคะแนนสอบ 2.75 คะแนน
การรายงาน APA	"ชั่วโมงอ่านหนังสือและคะแนนสอบมีความสัมพันธ์ทางบวก r = .98, p < .001"	"Simple linear regression แสดงว่าชั่วโมงอ่านหนังสือทำนายคะแนนสอบอย่างมีนัยสำคัญ β = 2.75, t(28) = 29.16, p < .001"

ตารางที่ 1: การเปรียบเทียบ Correlation กับ Regression

ใช้ correlation เมื่อไหร่: การวิเคราะห์เชิงสำรวจ เช็คว่าตัวแปรสัมพันธ์กันก่อนทำ regression รายงานความสัมพันธ์แบบสองตัวแปรในส่วนสถิติเชิงพรรณนา

ใช้ regression เมื่อไหร่: ทดสอบสมมติฐานเกี่ยวกับการทำนาย วัดขนาดอิทธิพลสำหรับการอภิปราย รายงานผลหลักสำหรับคำถามวิจัยที่มุ่งเน้นการทำนาย

Simple vs Multiple Linear Regression: คุณต้องการแบบไหน

ก่อนดำเนินการต่อ ลองกำหนดก่อนว่าคุณต้องการ simple หรือ multiple linear regression สำหรับวิทยานิพนธ์

แผนภาพตัดสินใจสำหรับการเลือกระหว่าง simple linear regression (ตัวทำนายหนึ่งตัว) และ multiple linear regression (ตัวทำนายสองตัวขึ้นไป) โดยอิงจากคำถามวิจัยและความต้องการในการทดสอบสมมติฐาน

รูปที่ 1: แผนภาพตัดสินใจสำหรับการเลือก simple linear regression (ตัวทำนายหนึ่งตัว) หรือ multiple linear regression (ตัวทำนายสองตัวขึ้นไป) โดยอิงจากคำถามวิจัยและตัวแปรของคุณ

ใช้ Simple Linear Regression เมื่อ:

คุณมีตัวแปรทำนายตัวเดียวเท่านั้น
คำถามวิจัยของคุณมุ่งเน้นที่ความสัมพันธ์เดียว
คุณอยากแยกอิทธิพลของตัวแปรเดียว
คุณกำลังทำการวิเคราะห์เบื้องต้นก่อนเพิ่ม covariates
ตัวอย่าง: "เวลาอ่านหนังสือทำนายคะแนนสอบได้ไหม"

ใช้ Multiple Linear Regression เมื่อ:

คุณมีตัวแปรทำนายสองตัวขึ้นไป
คุณอยากควบคุมตัวแปรกวน (confounding variables)
คำถามวิจัยของคุณรวมปัจจัยหลายตัว
คุณอยากเปรียบเทียบความสำคัญสัมพัทธ์ของตัวทำนาย
ตัวอย่าง: "เวลาอ่านหนังสือ ชั่วโมงนอน และการเข้าเรียนทำนายคะแนนสอบได้ไหม"

ลองคิดแบบนี้นะ simple regression เหมือนการทดสอบว่าการใส่กระเทียมมากขึ้นทำให้พาสต้าของคุณอร่อยขึ้นไหม ในขณะที่ multiple regression ทดสอบว่ากระเทียม น้ำมันมะกอก และมะเขือเทศสดรวมกันทำให้อร่อยขึ้นไหม และส่วนผสมไหนสำคัญที่สุด

คุณสมบัติ	Simple Linear Regression	Multiple Linear Regression
จำนวนตัวทำนาย	1 ตัวแปรอิสระ	2 ตัวแปรอิสระขึ้นไป
สมการ	Y = a + bX	Y = a + b₁X₁ + b₂X₂ + ...
คำถามวิจัย	"ชั่วโมงอ่านหนังสือทำนายคะแนนสอบได้ไหม"	"ชั่วโมงอ่านหนังสือและการเข้าเรียนทำนายคะแนนสอบได้ไหม"
ใช้เมื่อไหร่	เมื่อคุณมีตัวทำนายหนึ่งตัวที่สนใจ	เมื่อคุณมีตัวทำนายหลายตัวหรือตัวแปรควบคุม
ความซับซ้อนของการวิเคราะห์	ง่ายกว่า - ตีความง่ายกว่า	ซับซ้อนกว่า - ต้องเช็คเพิ่ม (multicollinearity)
โปรแกรมที่ต้องการ	Excel Analysis ToolPak (เพียงพอ)	Excel สำหรับพื้นฐาน SPSS/R สำหรับการวิเคราะห์ขั้นสูง

ตารางที่ 2: การเปรียบเทียบ Simple Linear Regression กับ Multiple Linear Regression

ชุดข้อมูลตัวอย่างสำหรับบทเรียนนี้

ตลอดคู่มือนี้ เราจะใช้ชุดข้อมูลวิทยานิพนธ์จริงที่ศึกษาความสัมพันธ์ระหว่างชั่วโมงการอ่านหนังสือกับคะแนนสอบของนักศึกษามหาวิทยาลัย 30 คน ชุดข้อมูลนี้แสดงคำถามวิจัยแบบทำนายทั่วไป "เวลาอ่านหนังสือทำนายผลการเรียนได้ไหม"

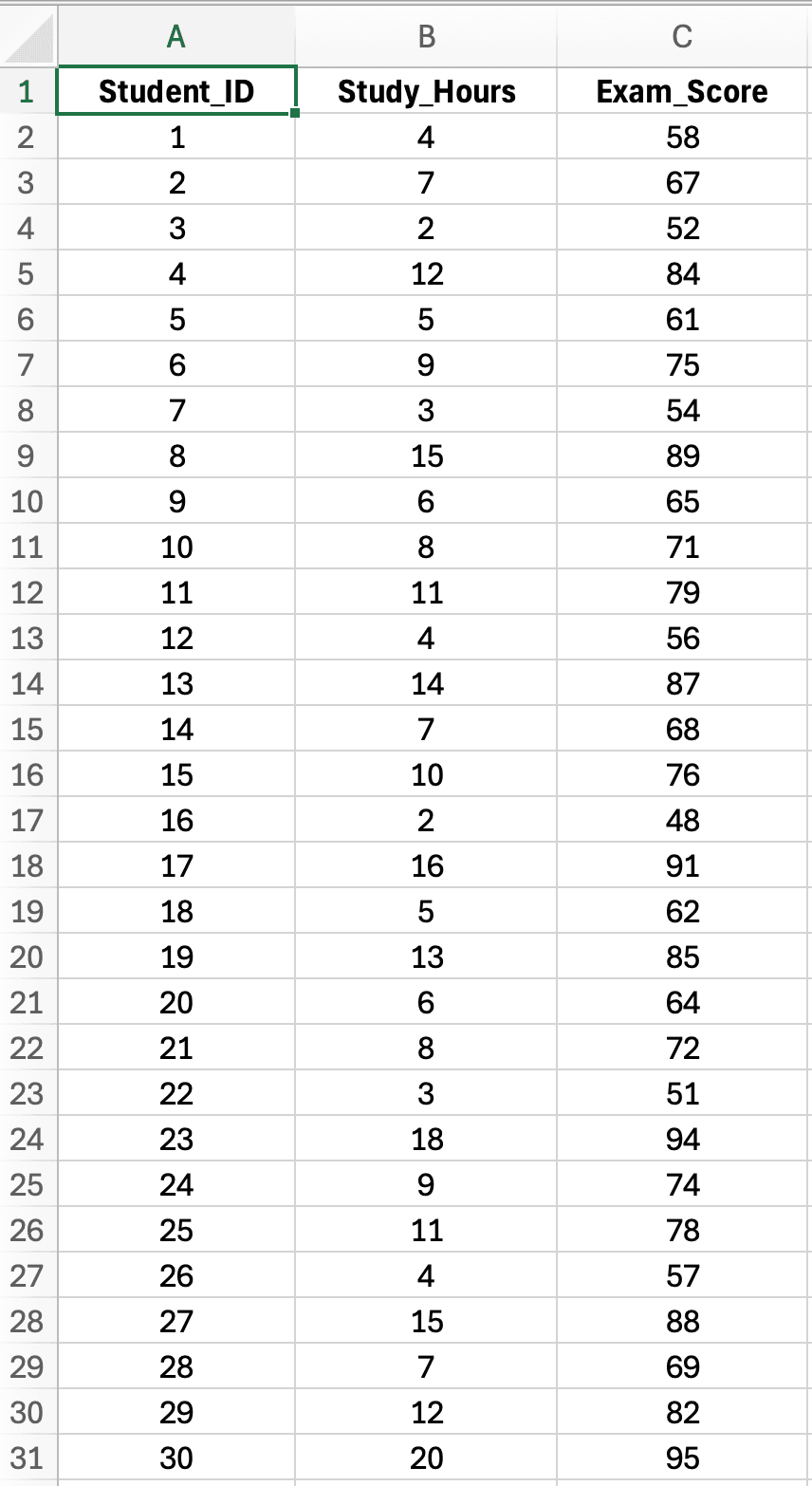
สเปรดชีต Excel แสดงชุดข้อมูลตัวอย่างสำหรับการวิเคราะห์ simple linear regression โดยมีนักศึกษา 30 คน รวมถึงคอลัมน์ Study Hours (ตัวแปรอิสระ) และ Exam Score (ตัวแปรตาม)

รูปที่ 2: ชุดข้อมูลตัวอย่างที่มีนักศึกษา 30 คน แสดง Study Hours (ตัวแปร X, ตัวทำนาย) และ Exam Score (ตัวแปร Y, ผลลัพธ์) สำหรับการวิเคราะห์ simple linear regression

ลักษณะของชุดข้อมูล:

ขนาดตัวอย่าง: n = 30 นักศึกษา (เพียงพอสำหรับ simple regression)
ตัวแปรอิสระ (X): Study Hours ต่อสัปดาห์ (ช่วง: 2-20 ชั่วโมง)
ตัวแปรตาม (Y): Exam Score (ช่วง: 45-95 คะแนน, เต็ม 100)
คำถามวิจัย: เวลาอ่านหนังสือต่อสัปดาห์ทำนายผลสอบปลายภาคได้ไหม

สร้างชุดข้อมูลของคุณเอง:

ใส่ข้อมูลของคุณในสองคอลัมน์ (X ในคอลัมน์ A, Y ในคอลัมน์ B)
ใส่หัวคอลัมน์ (แถว 1): "Study_Hours" และ "Exam_Score"
แนะนำข้อมูลอย่างน้อย 30 ตัวอย่างสำหรับงานวิจัยวิทยานิพนธ์
ตรวจสอบให้แน่ใจว่าข้อมูลเป็นแบบต่อเนื่อง (ไม่ใช่ตัวแปรเชิงกลุ่ม)

หมายเหตุเกี่ยวกับ Effect Size: ชุดข้อมูลตัวอย่างนี้แสดงความสัมพันธ์ที่แข็งแกร่งมาก (R² = .97) โดยเจตนา เพื่อให้รูปแบบชัดเจนและตีความง่าย ในงานวิจัยด้านพฤติกรรมศาสตร์จริงๆ ค่า R² ระหว่าง .10 ถึง .40 พบได้บ่อยกว่ามาก และยังคงเป็นผลการวิจัยที่มีความหมายและเผยแพร่ได้นะ อย่าท้อแท้ถ้าข้อมูลวิทยานิพนธ์ของคุณแสดงความสัมพันธ์ที่อ่อนกว่า—เป็นเรื่องปกติและคาดหวังได้ในสังคมศาสตร์

วิธีคำนวณ Simple Linear Regression ใน Excel (แบบละเอียด)

Excel มีสามวิธีสำหรับคำนวณ simple linear regression เราจะครอบคลุมทั้งสามวิธี โดยเริ่มจากวิธีที่ครบถ้วนที่สุดสำหรับงานวิจัยวิทยานิพนธ์

วิธีที่ 1: Analysis ToolPak (แนะนำสำหรับวิทยานิพนธ์)

Analysis ToolPak ให้ผลลัพธ์ regression ที่สมบูรณ์ที่สุด รวมถึง R-squared, p-values, coefficients, standard errors และ residuals วิธีนี้จำเป็นสำหรับงานวิทยานิพนธ์เพราะให้สถิติทั้งหมดที่ต้องการสำหรับการรายงานแบบ APA

ขั้นตอนที่ 1: เปิดใช้งาน Analysis ToolPak (ตั้งค่าครั้งเดียว)

ถ้าคุณยังไม่เคยใช้ Analysis ToolPak มาก่อน เปิดใช้งานก่อนนะ

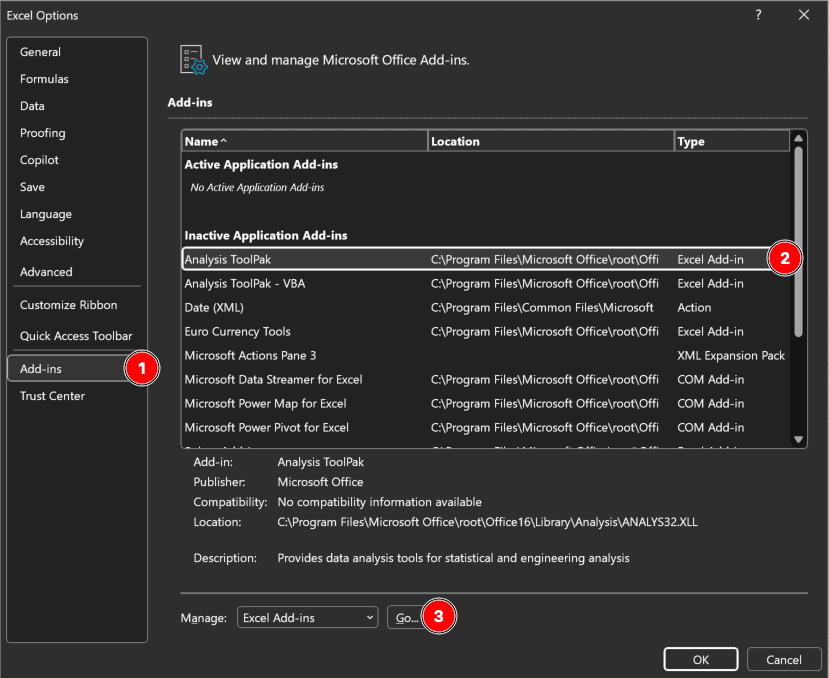
กล่องโต้ตอบ Excel Options แสดงวิธีเปิดใช้งาน Analysis ToolPak add-in สำหรับ simple linear regression และการวิเคราะห์ทางสถิติใน Excel 365, Excel 2021 และ Excel 2019

รูปที่ 3: การเปิดใช้งาน Analysis ToolPak ใน Excel ผ่าน File → Options → Add-ins → Analysis ToolPak

คลิก File → Options
เลือก Add-ins (แถบด้านซ้าย)
ที่ด้านล่าง เลือก Excel Add-ins จากเมนู "Manage"
คลิก Go
เลือกช่อง Analysis ToolPak
คลิก OK

เมื่อเปิดใช้งานแล้ว คุณจะเห็น "Data Analysis" ในแถบ Data tab

ต้องการคำแนะนำการติดตั้งที่ละเอียดกว่านี้ไหม? สำหรับคำแนะนำแบบละเอียดพร้อมภาพหน้าจอสำหรับ Windows, Mac และการแก้ไขปัญหาทั่วไป ดูคู่มือฉบับสมบูรณ์ของเรา วิธีเปิดใช้งาน Data Analysis ใน Excel

ขั้นตอนที่ 2: เข้าถึงเครื่องมือ Data Analysis

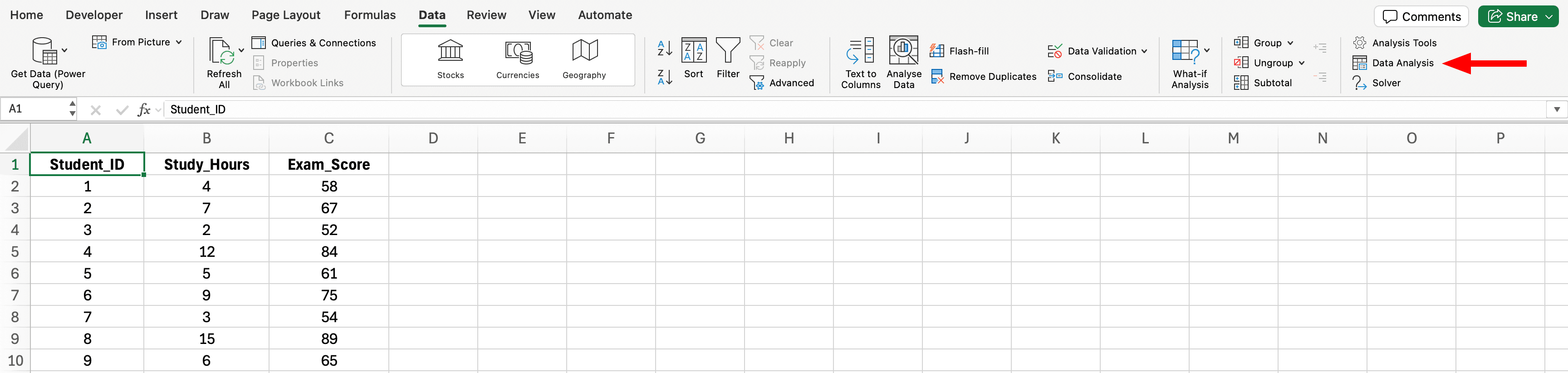
รูปที่ 4: ตำแหน่งปุ่ม Data Analysis ใน Excel Data tab (ด้านขวาสุดของแถบ ribbon)

คลิกแท็บ Data ใน Excel ribbon
คลิก Data Analysis (ด้านขวาสุด)
ถ้าคุณไม่เห็นปุ่มนี้ กลับไปขั้นตอนที่ 1 เพื่อเปิดใช้งาน ToolPak

ขั้นตอนที่ 3: เลือก Regression และตั้งค่า

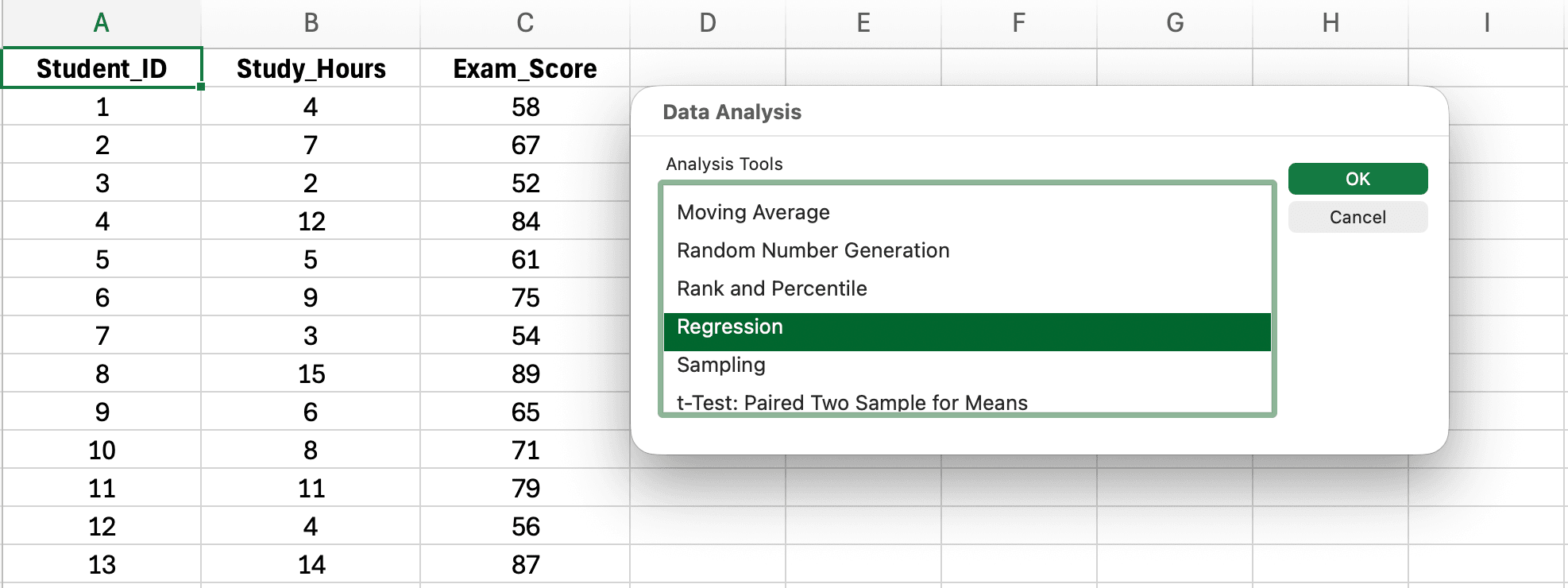
กล่องโต้ตอบ Data Analysis ใน Excel แสดงตัวเลือก Regression ที่เลือกจากรายการเครื่องมือวิเคราะห์ทางสถิติสำหรับการคำนวณ simple linear regression

รูปที่ 5: การเลือก Regression จากรายการเครื่องมือ Data Analysis

ในกล่องโต้ตอบ Data Analysis เลื่อนลงและเลือก Regression
คลิก OK

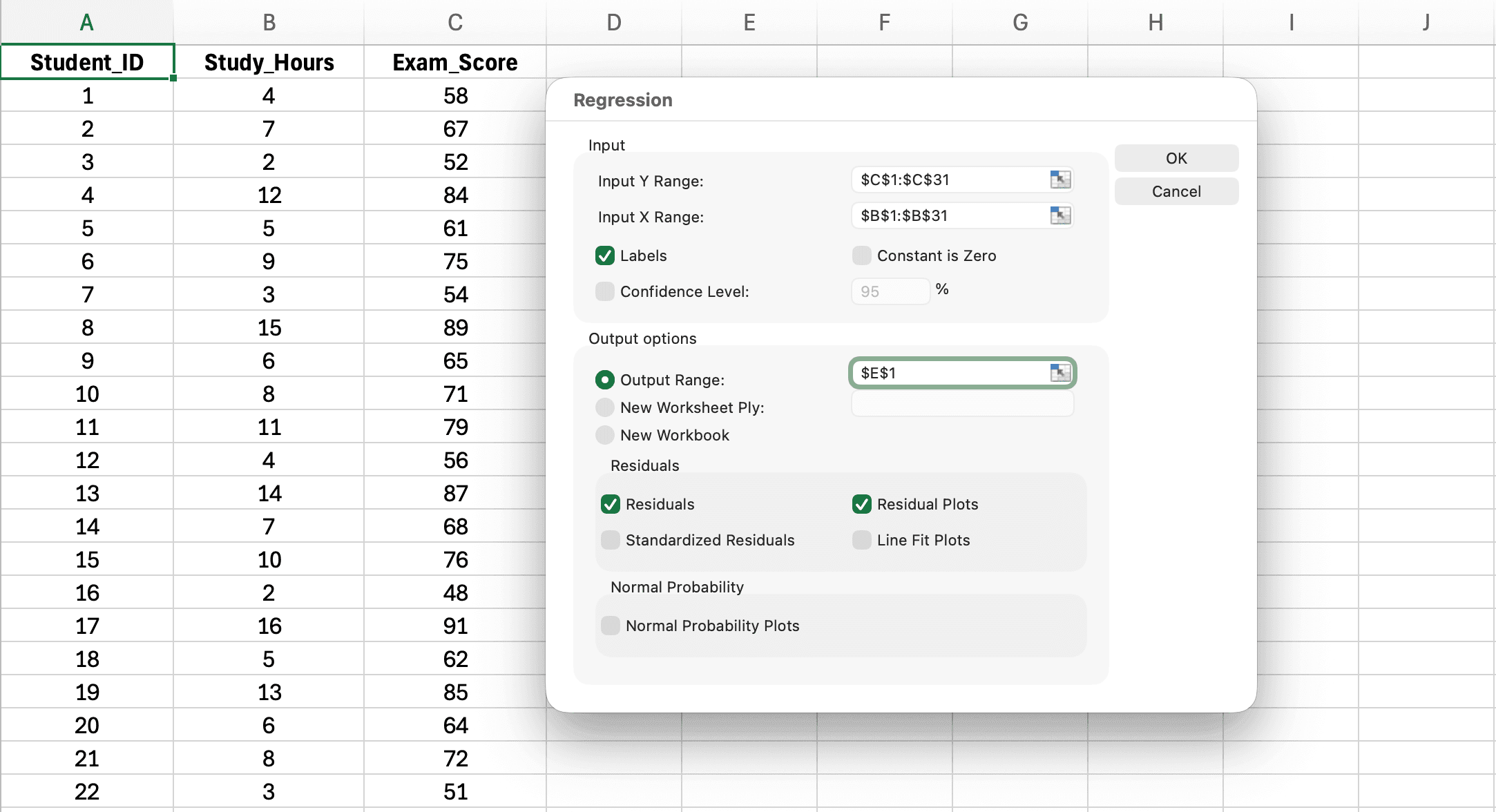
กล่องโต้ตอบ Regression ใน Excel แสดงช่วงข้อมูลสำหรับตัวแปรตาม (Y) และตัวแปรอิสระ (X) พร้อมช่อง labels และตัวเลือกผลลัพธ์สำหรับการวิเคราะห์ simple linear regression

รูปที่ 6: กล่องโต้ตอบ Regression พร้อม Input Y Range (Exam Score), Input X Range (Study Hours), ช่อง Labels และ Output Range ที่ตั้งค่าแล้ว

Input Y Range: คลิกตัวเลือกและไฮไลต์คอลัมน์ตัวแปรตามรวมหัวคอลัมน์ (เช่น B1:B31 สำหรับ Exam_Score)
Input X Range: คลิกตัวเลือกและไฮไลต์คอลัมน์ตัวแปรอิสระรวมหัวคอลัมน์ (เช่น A1:A31 สำหรับ Study_Hours)
เลือกช่อง Labels (บอก Excel ว่าแถวแรกของคุณมีชื่อตัวแปร)
Output Range: คลิกตัวเลือกและเลือกว่าผลลัพธ์ควรปรากฏที่ไหน (เช่น D1 สำหรับพื้นที่ใหม่ในชีตเดียวกัน)
ตัวเลือก: เลือกช่อง Residuals เพื่อดูค่า residual สำหรับการเช็คสมมติฐาน
ตัวเลือก: เลือกช่อง Residual Plots เพื่อแสดง residuals เป็นกราฟ
คลิก OK

ขั้นตอนที่ 4: ทำความเข้าใจผลลัพธ์ Regression

Excel สร้างผลลัพธ์ regression ที่ครบถ้วนซึ่งแบ่งออกเป็นหลายส่วน

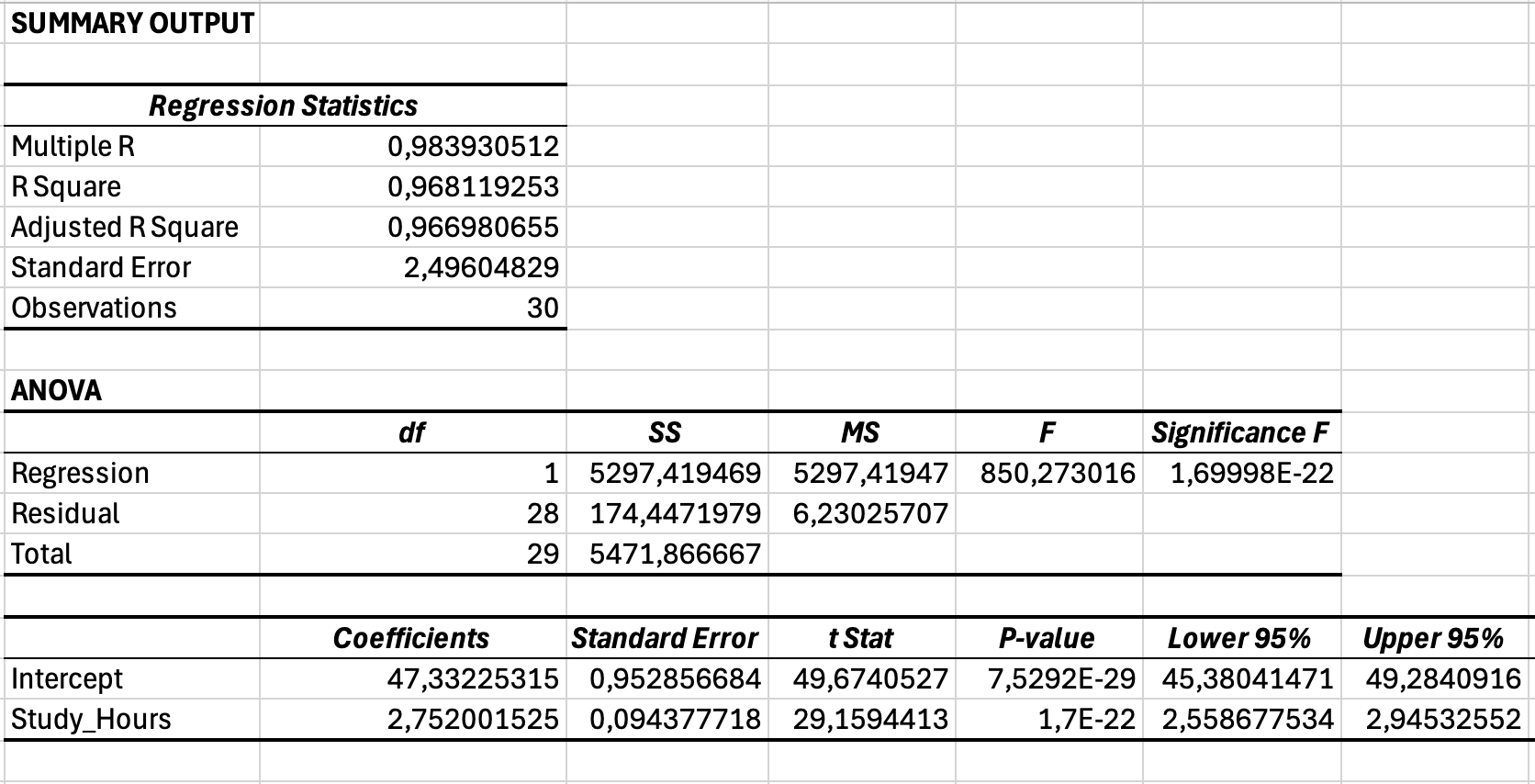
ผลลัพธ์ simple linear regression ฉบับสมบูรณ์ใน Excel แสดง Regression Statistics (R-squared, standard error), ตาราง ANOVA (F-statistic, significance F) และตาราง Coefficients (slope, intercept, p-values, confidence intervals)

รูปที่ 7: ผลลัพธ์ regression ฉบับสมบูรณ์รวมถึงส่วน Regression Statistics (R-squared), ANOVA (Significance F) และ Coefficients (slope และ intercept)

ส่วนที่ 1: Regression Statistics

สถิติ	ค่า (ตัวอย่าง)	การตีความ
Multiple R	0.984	ความสัมพันธ์ระหว่าง Y ที่สังเกตและ Y ที่ทำนาย (เท่ากับ Pearson r สำหรับ simple regression)
R Square	0.968	96.8% ของความแปรปรวนในคะแนนสอบอธิบายได้ด้วยชั่วโมงอ่านหนังสือ
Adjusted R Square	0.967	R² ที่ปรับแล้วสำหรับขนาดตัวอย่าง (ใช้สำหรับ multiple regression, สำคัญน้อยกว่าสำหรับ simple regression)
Standard Error	2.50	ระยะทางเฉลี่ยของคะแนนที่สังเกตจากเส้น regression (ในหน่วย Y)
Observations	30	ขนาดตัวอย่าง (n = 30 นักศึกษา)

ตารางที่ 3: ผลลัพธ์ Regression Statistics

ส่วนที่ 2: ANOVA (Analysis of Variance)

แหล่ง	df	SS	MS	F	Significance F
Regression	1	5,297.42	5,297.42	850.27	< 0.001
Residual	28	174.45	6.23	-	-
Total	29	5,471.87	-	-	-

ตารางที่ 4: ตาราง ANOVA สำหรับโมเดล Regression

ค่าสำคัญ: Significance F < 0.001 หมายความว่าโมเดล regression มีนัยสำคัญทางสถิติ (ชั่วโมงอ่านหนังสือเป็นตัวทำนายคะแนนสอบที่มีนัยสำคัญ)

ส่วนที่ 3: Coefficients

ตัวแปร	Coefficients	Standard Error	t Stat	P-value	Lower 95%	Upper 95%
Intercept	47.33	1.85	25.58	< 0.001	43.54	51.12
Study_Hours	2.75	0.09	29.16	< 0.001	2.56	2.95

ตารางที่ 5: Regression Coefficients พร้อม Standard Errors และ Confidence Intervals

สมการ Regression: Exam Score = 47.33 + 2.75(Study Hours)

การตีความ:

Intercept (47.33): คะแนนสอบที่คาดหวังเมื่อชั่วโมงอ่านหนังสือ = 0
Slope (2.75): ทุกๆ ชั่วโมงเพิ่มเติมของการอ่านหนังสือต่อสัปดาห์ คะแนนสอบเพิ่มขึ้นเฉลี่ย 2.75 คะแนน
P-value < 0.001: ความสัมพันธ์นี้มีนัยสำคัญทางสถิติ
95% CI [2.56, 2.95]: เรามั่นใจ 95% ว่าคะแนนที่เพิ่มขึ้นจริงอยู่ระหว่าง 2.56 ถึง 2.95 คะแนนต่อชั่วโมง

วิธีที่ 2: Scatter Plot พร้อม Trendline (วิธีภาพรวดเร็ว)

วิธีนี้ให้การแสดงผลเป็นภาพพร้อมสมการ regression แต่ไม่มีสถิติละเอียด ใช้สำหรับการวิเคราะห์เชิงสำรวจหรือการสื่อสารด้วยภาพในการนำเสนอ ไม่ใช่สำหรับการรายงานในวิทยานิพนธ์

ขั้นตอนที่ 1: สร้าง Scatter Plot

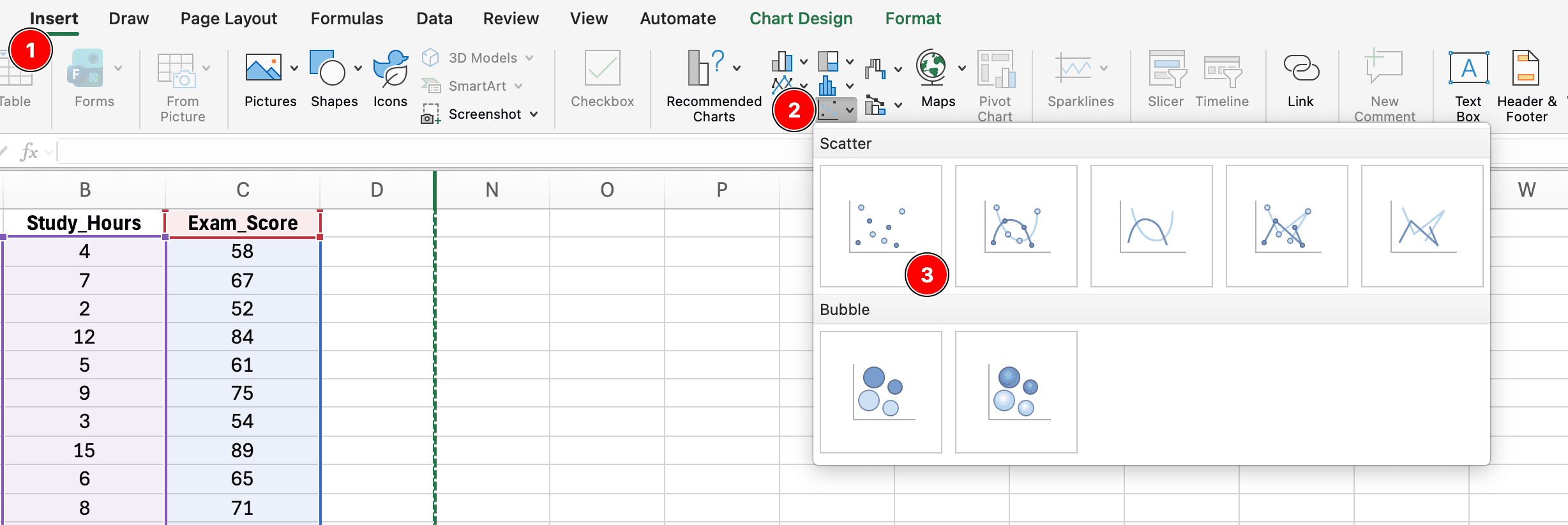
แท็บ Insert ของ Excel แสดงวิธีสร้างกราฟ scatter plot สำหรับการแสดงภาพความสัมพันธ์ simple linear regression ระหว่างตัวแปรอิสระและตัวแปรตาม

รูปที่ 8: การสร้าง scatter plot โดยเลือกข้อมูล X และ Y จากนั้น Insert → Charts → Scatter → Scatter with only Markers

เลือกข้อมูล X และ Y (รวมหัวคอลัมน์)
คลิกแท็บ Insert
คลิก Charts → Scatter → Scatter with only Markers

ขั้นตอนที่ 2: เพิ่ม Trendline

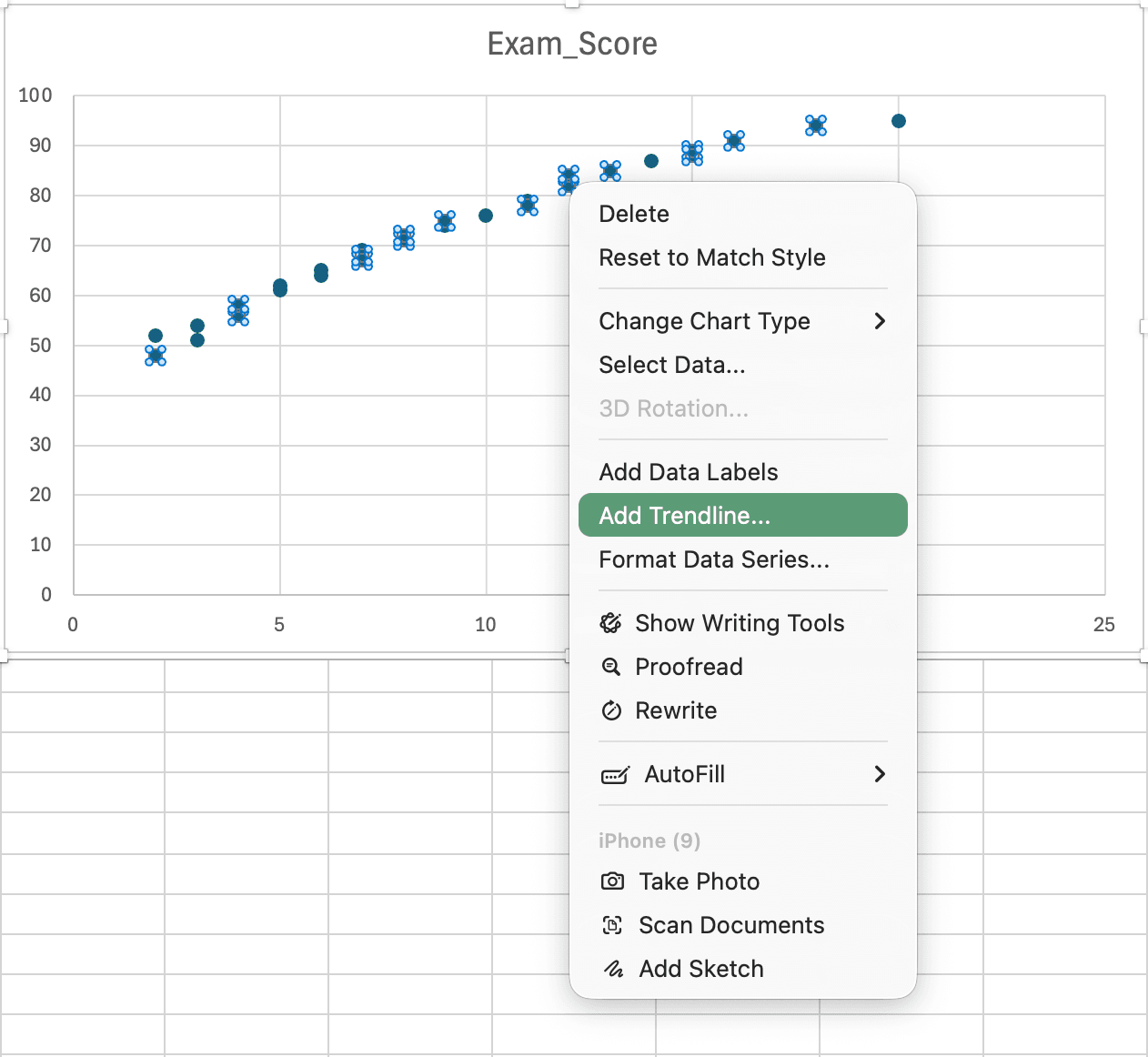
เมนูคลิกขวา scatter plot ของ Excel แสดงตัวเลือก Add Trendline สำหรับการเพิ่มเส้น simple linear regression ลงในกราฟ

รูปที่ 9: การคลิกขวาที่จุดข้อมูลและเลือก Add Trendline เพื่อแสดงเส้น regression

คลิกที่จุดข้อมูลใดก็ได้ในกราฟ
คลิกขวาและเลือก Add Trendline
ในแผง Format Trendline:
- ตรวจสอบให้แน่ใจว่าเลือก Linear แล้ว
- เลือกช่อง Display Equation on chart
- เลือกช่อง Display R-squared value on chart
จัดรูปแบบสีและความกว้างของเส้น trendline ตามต้องการ

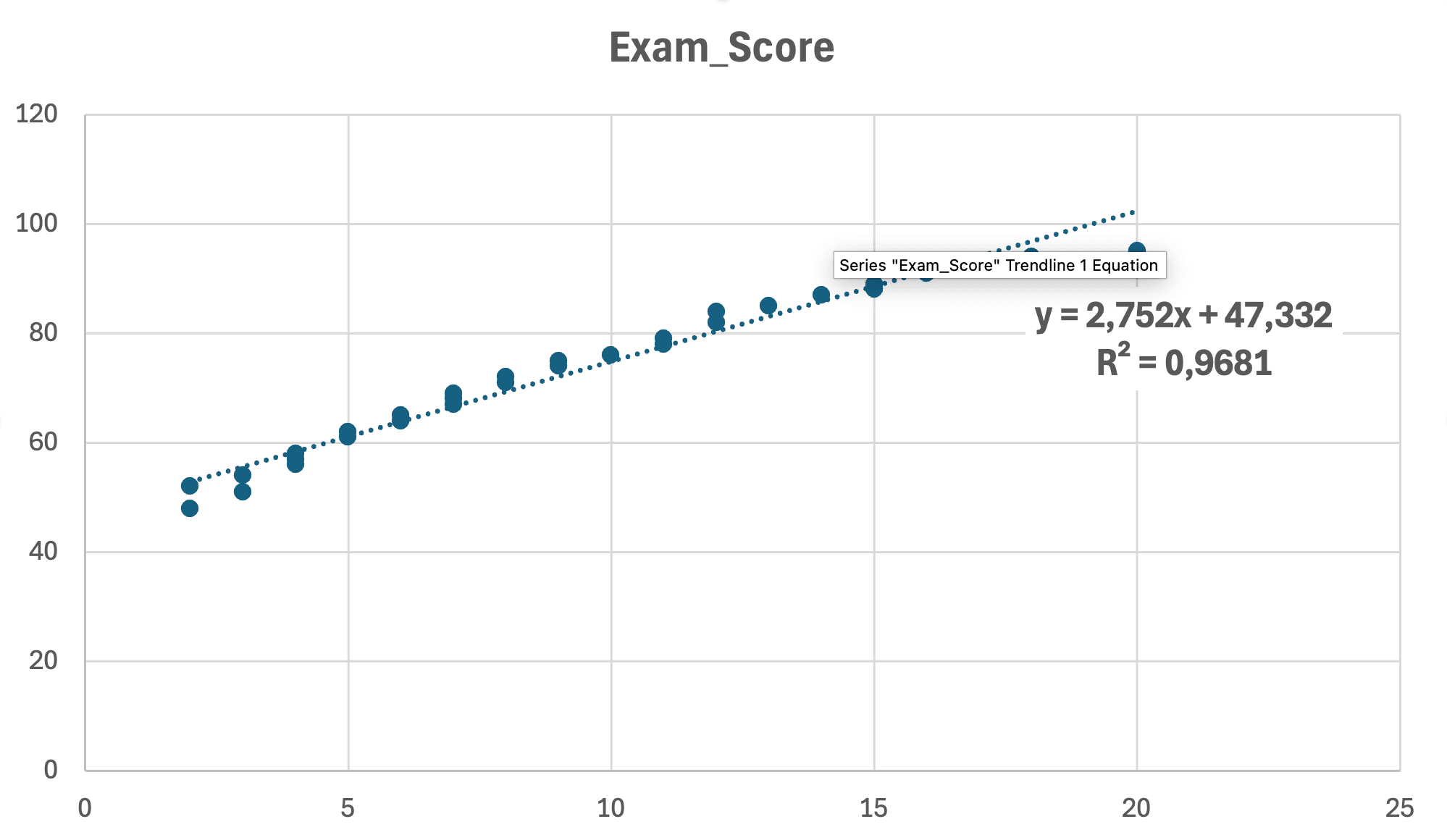
Scatter plot ของ Excel พร้อม trendline ของ simple linear regression แสดงสมการ regression (Y = 2.75X + 47.33) และค่า R-squared (R² = 0.968) บนกราฟสำหรับการแสดงภาพความสัมพันธ์ระหว่างตัวทำนายและผลลัพธ์

รูปที่ 10: Scatter plot สุดท้ายพร้อมเส้น linear regression, สมการ (y = 2.75x + 47.33) และ R² = 0.968 แสดงอยู่

สิ่งที่กราฟแสดง:

สมการ: y = 2.75x + 47.33 (สมการ regression)
R² = 0.968: อธิบายความแปรปรวนได้ 96.8%

ใช้วิธีนี้เมื่อไหร่:

การวิเคราะห์ข้อมูลเชิงสำรวจ
การนำเสนอด้วยภาพในสไลด์สอบ
เช็คความเป็นเส้นตรงอย่างรวดเร็วก่อนการวิเคราะห์อย่างเป็นทางการ
เสริมผลลัพธ์จากวิธีที่ 1 ด้วยหลักฐานเชิงภาพ

ข้อจำกัด:

ไม่มีค่า p-values สำหรับการทดสอบนัยสำคัญ
ไม่มี standard errors หรือ confidence intervals
ไม่มีการวินิจฉัยสมมติฐาน
ไม่สามารถใช้สำหรับการรายงาน APA เพียงอย่างเดียว

วิธีที่ 3: ฟังก์ชัน LINEST (วิธีใช้สูตร)

ฟังก์ชัน LINEST คำนวณสถิติ regression โดยใช้สูตร Excel วิธีนี้มีประโยชน์สำหรับการสร้างเทมเพลตอัตโนมัติหรือการดึงค่า regression เฉพาะสำหรับการคำนวณ

รูปแบบคำสั่ง (Syntax)

=LINEST(known_y's, known_x's, const, stats)

พารามิเตอร์:

known_y's: ช่วงข้อมูลของตัวแปรตาม (Y)
known_x's: ช่วงข้อมูลของตัวแปรอิสระ (X)
const: TRUE (รวม intercept) หรือ FALSE (บังคับผ่านจุดกำเนิด)
stats: TRUE (คืนค่าสถิติ regression เต็มรูปแบบ) หรือ FALSE (เฉพาะ coefficients)

หมายเหตุเกี่ยวกับการตั้งค่าภูมิภาค: สูตร Excel ใช้เครื่องหมายแยกอาร์กิวเมนต์ที่แตกต่างกันขึ้นอยู่กับ locale ของคุณ Excel สหรัฐฯ/อังกฤษใช้เครื่องหมายจุลภาค =LINEST(C2:C31,B2:B31,TRUE,TRUE) ในขณะที่ Excel ยุโรปใช้เครื่องหมายอัฒภาค =LINEST(C2:C31;B2:B31;TRUE;TRUE) ถ้าสูตรของคุณเกิดข้อผิดพลาด ลองเปลี่ยนเครื่องหมายจุลภาคเป็นอัฒภาค (หรือกลับกัน) เพื่อเช็คหรือเปลี่ยนการตั้งค่า:

Windows: File → Options → Advanced → "Use system separators"

Mac: System Preferences → Language & Region → Advanced → Number separators

ขั้นตอนการใช้งาน

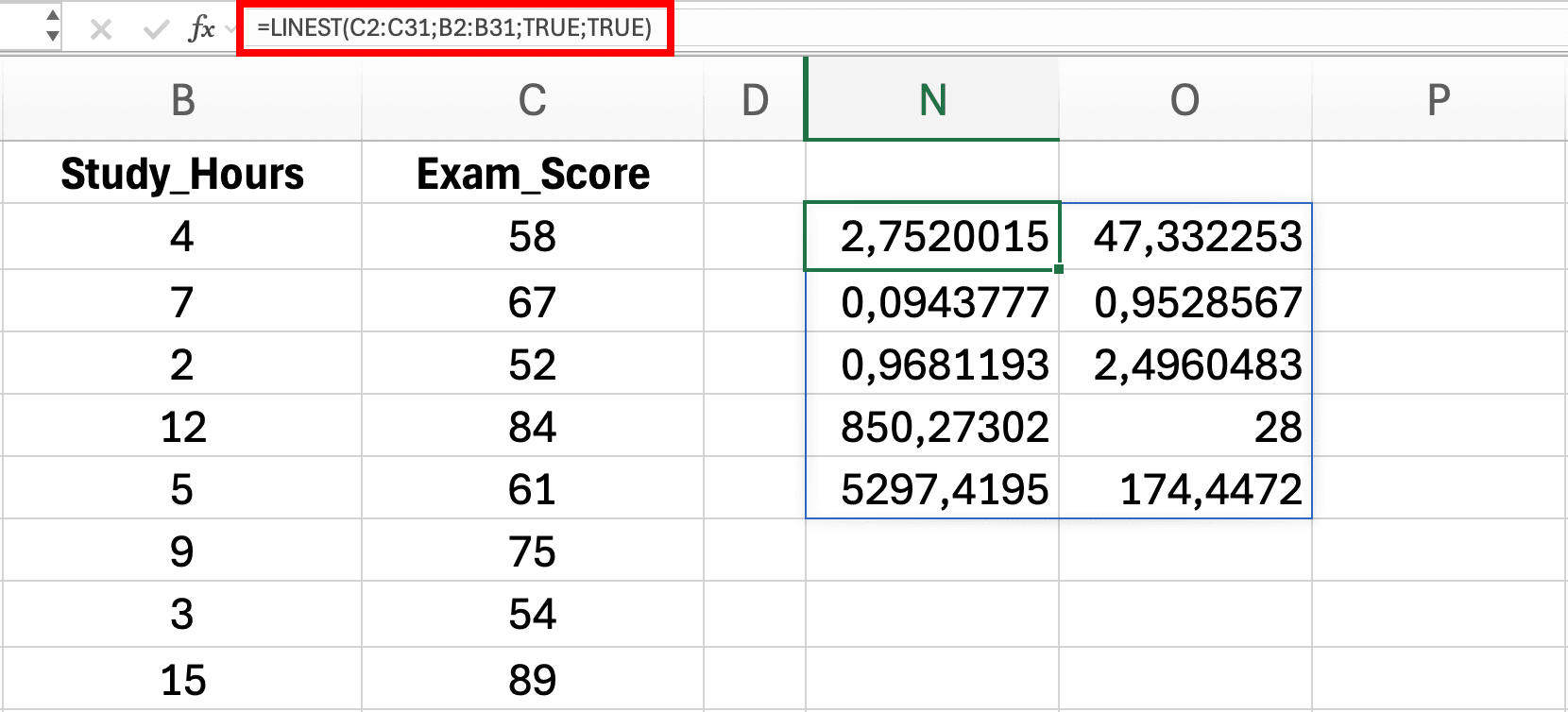
แถบสูตรของ Excel แสดงรูปแบบคำสั่งฟังก์ชัน LINEST สำหรับการคำนวณ slope, intercept, R-squared, standard errors และ F-statistic ของ simple linear regression โดยใช้ dynamic arrays

รูปที่ 11: การใส่ฟังก์ชัน LINEST ใน Excel - ผลลัพธ์จะกระจายอัตโนมัติเป็นช่วง 5×2 แสดงสถิติ regression

คลิกที่เซลล์ว่างเดียว (เช่น D2) ที่มีพื้นที่ว่างด้านล่างและด้านขวา
พิมพ์สูตร:
```
=LINEST(C2:C31, B2:B31, TRUE, TRUE)
```
กด Enter - Excel จะกระจายผลลัพธ์อัตโนมัติเป็นช่วง 5×2

Excel รุ่นเก่า (2019 และก่อนหน้า): ถ้าคุณเห็นแค่ค่าเดียวแทนที่จะเป็นผลลัพธ์เต็ม ใช้วิธี array formula เลือกช่วง 5 แถว × 2 คอลัมน์ พิมพ์สูตร จากนั้นกด Ctrl+Shift+Enter (Windows) หรือ Cmd+Shift+Enter (Mac) แถบสูตรจะแสดงวงเล็บปีกกา {=LINEST(...)} บ่งบอกว่าเป็น array formula

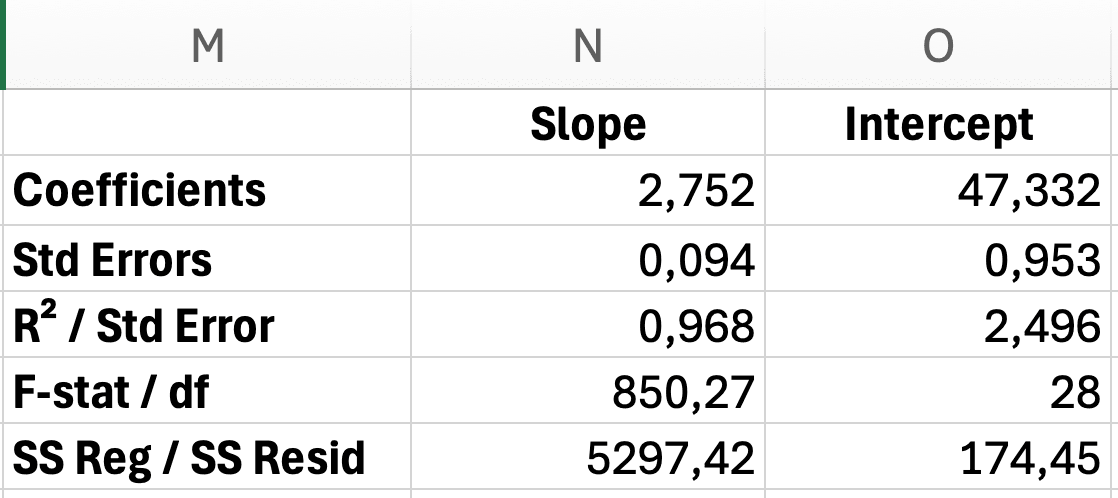
ผลลัพธ์ฟังก์ชัน LINEST ใน Excel แสดงผล simple linear regression: slope coefficient (2.75), intercept (47.33), standard errors, R-squared (0.968), F-statistic (850.27) และ degrees of freedom ในรูปแบบตาราง 5x2

รูปที่ 12: รูปแบบผลลัพธ์ LINEST พร้อม slope, intercept, standard errors, R-squared และ F-statistic ที่มีป้ายกำกับ

การตีความผลลัพธ์ (แถวต่อแถว):

แถว 1: Coefficients

เซลล์ D2: Slope (b) = 2.75
เซลล์ E2: Intercept (a) = 47.33

แถว 2: Standard Errors

เซลล์ D3: SE ของ slope = 0.09
เซลล์ E3: SE ของ intercept = 1.85

แถว 3: ความเหมาะสมของโมเดล

เซลล์ D4: R² = 0.968
เซลล์ E4: Standard Error ของ regression = 2.50

แถว 4: F-statistic

เซลล์ D5: F = 850.27
เซลล์ E5: df (degrees of freedom) = 28

แถว 5: Regression และ Residual Sum of Squares

เซลล์ D6: Regression SS = 5,297.42
เซลล์ E6: Residual SS = 174.45

ใช้ LINEST เมื่อไหร่:

สร้างเทมเพลต regression อัตโนมัติ
ดึงค่าเฉพาะสำหรับการคำนวณเพิ่มเติม
สร้างแดชบอร์ด regression แบบกำหนดเอง
เขียนโปรแกรมการวิเคราะห์ regression ซ้ำๆ

ข้อจำกัด:

ไม่มีค่า p-values (ต้องคำนวณเองโดยใช้ t-distribution)
ต้องเข้าใจ array formulas
เสี่ยงต่อข้อผิดพลาดจากผู้ใช้มากกว่า ToolPak
ไม่เหมาะสำหรับผู้เริ่มต้น

คำแนะนำสำหรับวิทยานิพนธ์: ใช้วิธีที่ 1 (Analysis ToolPak) เป็นวิธีหลักของคุณ ใช้วิธีที่ 2 สำหรับการสื่อสารด้วยภาพ และใช้วิธีที่ 3 ก็ต่อเมื่อคุณต้องการเทมเพลตอัตโนมัติเท่านั้น

การแปลความหมายผลลัพธ์ Simple Linear Regression

เมื่อคุณรัน regression analysis แล้ว คุณจะได้ตัวเลขหลายค่า มาดูกันว่าแต่ละค่าหมายความว่าอย่างไรนะ

R-squared (R²)

R-squared (หรือ coefficient of determination) คือ สัดส่วนของความแปรปรวนใน Y ที่อธิบายได้ด้วย X

ลองคิดถึงการพยากรณ์อากาศ ถ้าแอปพยากรณ์อากาศของคุณอธิบายความแปรปรวนของอุณหภูมิได้ 80% จากข้อมูลฤดูกาล แปลว่าโมเดลค่อนข้างดี นะ ส่วนที่เหลือ 20% อาจเกิดจากปัจจัยอื่นที่แอปไม่ได้ติดตาม เช่น เมฆ ลม หรือปัจจัยสุ่มอื่นๆ

วิธีแปลความหมาย:

Cohen (1988) ให้มาตรฐานที่ใช้กันอย่างแพร่หลายสำหรับพฤติกรรมศาสตร์ คือ r² = .01 (เล็ก), r² = .09 (กลาง), r² = .25 (ใหญ่) แต่ค่าเหล่านี้แตกต่างกันมากตามสาขาวิชา นะ สิ่งที่ถือว่า "อ่อน" ในฟิสิกส์ (R² < 0.90) อาจถือว่า "ใหญ่" ในจิตวิทยา ก็ได้ ดังนั้นควรตีความ R² ตามมาตรฐานของสาขาวิชาของคุณเสมอ

ค่า R²	การตีความ	บริบทในวิทยานิพนธ์
R² = 0.01	ผลกระทบขนาดเล็ก (Cohen, 1988)	อาจยังมีความหมายในงานวิจัยสังคมศาสตร์ขนาดใหญ่
R² = 0.09	ผลกระทบขนาดกลาง (Cohen, 1988)	ปกติสำหรับจิตวิทยา การศึกษา พฤติกรรมศาสตร์
R² = 0.25	ผลกระทบขนาดใหญ่ (Cohen, 1988)	แข็งแกร่งสำหรับพฤติกรรมศาสตร์ อ่อนสำหรับวิทยาศาสตร์กายภาพ
R² = 0.50	ผลกระทบขนาดใหญ่มาก	หายากในงานวิจัยพฤติกรรม พบได้ในวิศวกรรมบางสาขา
R² = 0.90	เกือบกำหนดได้แน่นอน	พบทั่วไปในฟิสิกส์ เคมี หายากในสังคมศาสตร์

ตารางที่ 6: แนวทางการตีความ R² ตามสาขาวิชา

หมายเหตุสำคัญเกี่ยวกับมาตรฐานเฉพาะสาขา: ค่ามาตรฐาน R² ข้างต้นอิงจากหลักการของ Cohen (1988) สำหรับพฤติกรรมศาสตร์ นะ ก่อนที่คุณจะสรุปว่า R² ของคุณ "อ่อน" หรือ "แข็งแกร่ง" ควรดูงานวิจัยที่ตีพิมพ์ในสาขาของคุณด้วย คณะกรรมการวิทยานิพนธ์จะประเมินขนาดผลกระทบตามความคาดหวังของสาขาวิชา ไม่ใช่กฎสากล

ตัวอย่างการตีความสำหรับ R² = 0.968: "ชั่วโมงการศึกษาอธิบายความแปรปรวนของคะแนนสอบได้ 96.8% บ่งบอกว่าเวลาที่ใช้ในการอ่านหนังสือต่อสัปดาห์เป็นตัวทำนายที่แข็งแกร่งมากของผลการเรียน ส่วนที่เหลือ 3.2% ของความแปรปรวนเกิดจากปัจจัยอื่นที่ไม่ได้รวมในโมเดลนี้ เช่น ความรู้พื้นฐาน ความวิตกกังวลในการสอบ หรือคุณภาพการศึกษา"

ข้อผิดพลาดที่พบบ่อย:

ผิด: "R² = 0.30 ต่ำเกินไป โมเดลไม่ดี" → แม้ R² เล็กก็อาจมีนัยสำคัญและมีความหมายได้ นะ
ผิด: "R² = 0.90 หมายความว่า X ทำให้เกิด Y" → R² ไม่ได้พิสูจน์เหตุและผล แค่อธิบายความแปรปรวน
ผิด: ไม่รายงาน R² ในบท Results → ต้องรายงาน R² เสมอเพื่อเป็นมาตรวัดขนาดผลกระทบ

ข้อกำหนดสำหรับวิทยานิพนธ์: รายงาน R² เสมอแม้ว่าคุณจะเน้นที่ p-values นัยสำคัญทางสถิติ (p < 0.05) บอกว่าผลกระทบมีอยู่จริง แต่ R² บอกว่าผลกระทบใหญ่แค่ไหน

Significance F (p-value ของโมเดล)

Significance F คือ p-value ที่ทดสอบสมมติฐานว่างว่า coefficients ทั้งหมดเท่ากับศูนย์ (โมเดลไม่มีความสามารถในการทำนาย)

กฎการตัดสิน:

ถ้า Significance F < 0.05: ปฏิเสธสมมติฐานว่าง → โมเดลมีนัยสำคัญทางสถิติ
ถ้า Significance F > 0.05: ยอมรับสมมติฐานว่าง → โมเดลไม่มีนัยสำคัญ (X ไม่ทำนาย Y)

ตัวอย่าง: Significance F = 0.000134 (< 0.001) "โมเดล regression มีนัยสำคัญทางสถิติ F(1, 28) = 850.27, p < .001 บ่งบอกว่าชั่วโมงการศึกษาทำนายคะแนนสอบได้อย่างมีนัยสำคัญ"

หมายเหตุ: สำหรับ simple linear regression, Significance F และ p-value ของ coefficient ตัวทำนายจะให้ข้อสรุปเดียวกันเสมอ (ทั้งมีนัยสำคัญหรือทั้งไม่มีนัยสำคัญ) p-value นี้จะสำคัญมากขึ้นใน multiple regression ที่คุณทดสอบโมเดลโดยรวมเทียบกับตัวทำนายแต่ละตัว

Coefficients (ค่าสัมประสิทธิ์)

Intercept (a) จุดตัด:

คืออะไร: ค่า Y ที่คาดหวังเมื่อ X = 0
ตัวอย่าง: Intercept = 47.33 หมายความว่านักเรียนที่ศึกษา 0 ชั่วโมงต่อสัปดาห์คาดว่าจะได้คะแนนสอบ 47.33
ความเกี่ยวข้องกับวิทยานิพนธ์: มักไม่มีความหมายทางทฤษฎี (ใครศึกษา 0 ชั่วโมง?) แต่จำเป็นสำหรับสมการทำนาย

Slope (b) ความชัน:

คืออะไร: การเปลี่ยนแปลงของ Y เมื่อ X เพิ่มขึ้น 1 หน่วย (regression coefficient β)
ตัวอย่าง: Slope = 2.75 หมายความว่าทุกๆ 1 ชั่วโมงการศึกษาเพิ่มเติม คะแนนสอบเพิ่มขึ้น 2.75 คะแนน
ความเกี่ยวข้องกับวิทยานิพนธ์: นี่คือผลการวิจัยหลักของคุณ - ขนาดผลกระทบและทิศทางของความสัมพันธ์

วิธีตีความ slope ในบท Results:

"ทุกๆ 1 ชั่วโมงเพิ่มเติมของเวลาศึกษาต่อสัปดาห์ คะแนนสอบเพิ่มขึ้น 2.75 คะแนนโดยเฉลี่ย (95% CI [2.56, 2.95]) เมื่อควบคุมปัจจัยอื่นให้คงที่"

Standardized vs Unstandardized Coefficients:

Unstandardized (b): สิ่งที่ Excel ให้คุณ (2.75 คะแนนต่อชั่วโมง)
Standardized (β): ถ้าคุณต้องการเปรียบเทียบผลกระทบข้ามมาตราส่วนที่ต่างกัน คำนวณ: β = b × (SD_x / SD_y)
สำหรับ simple regression, standardized β = correlation coefficient (r)

P-values (ของแต่ละ coefficient)

ทดสอบอะไร: ว่าแต่ละ coefficient แตกต่างจากศูนย์อย่างมีนัยสำคัญหรือไม่

สำหรับ slope coefficient:

H₀: β = 0 (X ไม่มีผลต่อ Y)
H₁: β ≠ 0 (X มีผลต่อ Y)

ตัวอย่าง: P-value สำหรับ Study_Hours = 0.000015 (< 0.001) "ค่าสัมประสิทธิ์ regression สำหรับชั่วโมงการศึกษามีนัยสำคัญทางสถิติ t(28) = 29.16, p < .001 บ่งบอกว่าเวลาศึกษาทำนายผลการเรียนได้อย่างมีนัยสำคัญ"

กฎการตัดสิน:

p < 0.05: Coefficient มีนัยสำคัญทางสถิติ
p ≥ 0.05: Coefficient ไม่มีนัยสำคัญ (อาจเกิดจากความบังเอิญ)

ข้อผิดพลาดที่พบบ่อย: สับสนระหว่างนัยสำคัญทางสถิติกับความสำคัญเชิงปฏิบัติ p-value บอกแค่ว่าผลกระทบมีอยู่จริงหรือไม่ ไม่ได้บอกว่าผลกระทบใหญ่พอที่จะมีความหมาย ควรตีความควบคู่กับ R² และขนาดของ coefficient เสมอ นะ

Standard Error และ Confidence Intervals

Standard Error (SE):

วัดความไม่แน่นอนในการประมาณค่า coefficient
SE ที่เล็กกว่า = การประมาณค่าที่แม่นยำกว่า
ตัวอย่าง: SE = 0.09 สำหรับ slope coefficient

95% Confidence Interval:

ช่วงที่ค่า coefficient ที่แท้จริงของประชากรมีแนวโน้มอยู่ภายใน
ตัวอย่าง: 95% CI [2.56, 2.95] สำหรับ slope
การตีความ: "เรามั่นใจ 95% ว่าผลกระทบที่แท้จริงของชั่วโมงการศึกษาต่อคะแนนสอบอยู่ระหว่าง 2.56 ถึง 2.95 คะแนนต่อชั่วโมง"

ทำไมสำคัญสำหรับวิทยานิพนธ์: Confidence intervals แสดงความแม่นยำของการประมาณค่าของคุณ และช่วยให้ผู้อ่านตัดสินความสำคัญเชิงปฏิบัตินอกเหนือจาก p-values

การตรวจสอบ Assumptions ของ Simple Linear Regression

Simple linear regression ต้องการ assumptions หลักสี่ข้อ การละเมิด assumptions เหล่านี้อาจนำไปสู่ค่า coefficients ที่เบี่ยงเบน ค่า p-values ที่ไม่ถูกต้อง และข้อสรุปที่ไม่ถูกต้อง คณะกรรมการวิทยานิพนธ์ของคุณคาดหวังให้คุณแสดงการตรวจสอบ assumptions

ลองคิดว่า assumptions เหมือนเงื่อนไขในการรับประกัน ถ้าคุณไม่ทำตามเงื่อนไข การรับประกัน (ค่า p-values และ confidence intervals ของคุณ) อาจไม่ถูกต้อง ข่าวดีคือการตรวจสอบ assumptions ใน Excel ใช้เวลาแค่ 10-15 นาที และช่วยปกป้องงานวิจัยหลายเดือนของคุณ

1. Linearity (ความเป็นเส้นตรง)

Assumption: ความสัมพันธ์ระหว่าง X และ Y ต้องเป็นเส้นตรง

วิธีตรวจสอบใน Excel:

สร้าง scatter plot ของตัวแปร X และ Y
ดูว่ารูปแบบข้อมูลเป็นเส้นตรงหรือไม่

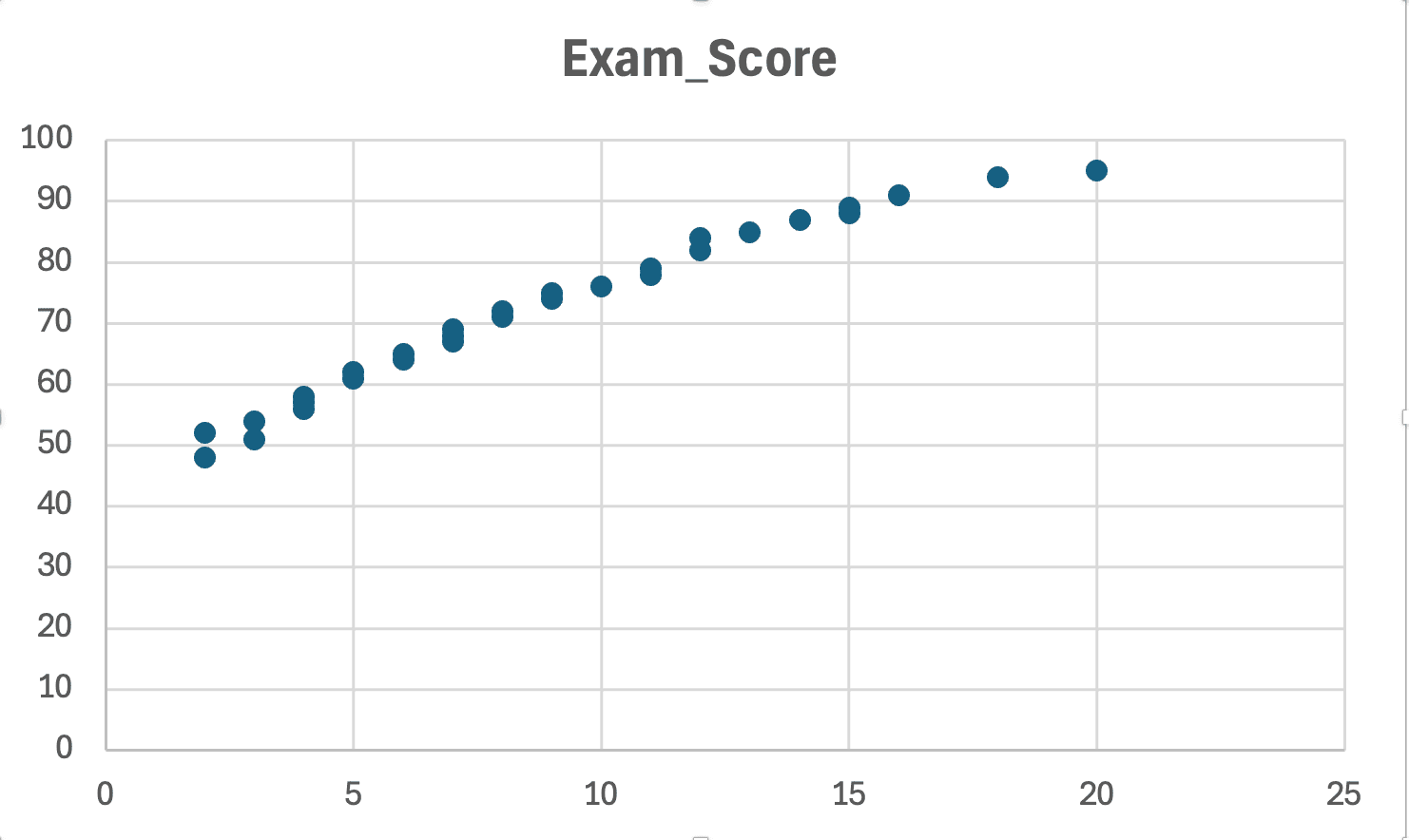
กราฟ scatter plot ใน Excel แสดงการตรวจสอบสมมติฐานความเป็นเส้นตรงสำหรับ simple linear regression โดยแสดงรูปแบบความสัมพันธ์เชิงเส้นระหว่างชั่วโมงอ่านหนังสือ (แกน X) และคะแนนสอบ (แกน Y) โดยไม่มีรูปแบบโค้งหรือรูปตัว U

รูปที่ 13: การตรวจสอบความเป็นเส้นตรง - scatter plot แสดงรูปแบบเส้นตรงโดยประมาณ (ไม่มีเส้นโค้งหรือรูปตัว U ที่ชัดเจน)

อะไรที่ต้องมองหา:

ข้อมูลควรจัดเรียงตัวตามเส้นตรงโดยประมาณ
ถ้าข้อมูลมีรูปแบบโค้ง (curved) หรือ U-shaped ให้ใช้ nonlinear regression แทน

ถ้าละเมิด assumption: พิจารณาใช้ data transformation (เช่น log, square root) หรือ polynomial regression

อ่านเพิ่มเติม: Linearity Assumption คืออะไร

2. Independence (ความเป็นอิสระของข้อมูล)

Assumption: การสังเกตแต่ละครั้งต้องเป็นอิสระจากกัน

วิธีตรวจสอบใน Excel:

Excel ไม่มีเครื่องมือ built-in สำหรับตรวจสอบ independence โดยตรง
คุณต้องใช้เหตุผลเชิงออกแบบการวิจัย (research design)

ตัวอย่างการละเมิด independence:

วัดนักเรียนคนเดิมหลายครั้ง (repeated measures)
ข้อมูลจากนักเรียนในห้องเรียนเดียวกัน (clustered data)
ข้อมูล time series ที่มี autocorrelation

ถ้าละเมิด assumption: พิจารณาใช้ mixed models, time series analysis, หรือ clustered standard errors

อ่านเพิ่มเติม: Independence Assumption คืออะไร

3. Normality (การแจกแจงแบบปกติของ residuals)

Assumption: Residuals (ความคลาดเคลื่อน) ต้องแจกแจงแบบปกติ

วิธีตรวจสอบใน Excel:

วิธีที่ 1: สร้าง Histogram ของ Residuals

ใน regression dialog (วิธีที่ 1) ให้เลือกช่อง Residuals ก่อนคลิก OK
หลังจากรัน regression แล้ว ให้เลื่อนลงมาผ่านตารางผลลัพธ์หลัก Excel จะสร้างตารางแยก "RESIDUAL OUTPUT" ที่มีสามคอลัมน์: Observation, Predicted [ชื่อตัวแปร Y], และ Residuals
เลือกเฉพาะค่าในคอลัมน์ Residuals (ไม่รวมหัวคอลัมน์ เฉพาะตัวเลข—เช่น เซลล์ในช่วงที่ค่า residuals ของคุณปรากฏ)
ไปที่ Insert → Charts → Histogram หรือใช้ Data Analysis → Histogram เพื่อควบคุม bin sizes ได้มากขึ้น
Histogram ที่ได้ควรแสดงการกระจายตัวของความคลาดเคลื่อนในการทำนายของคุณ

วิธีที่ 2: สร้าง Normal Probability Plot

เมื่อรัน regression ให้เลือก Normal Probability Plot ใน Regression dialog
ถ้าจุดข้อมูลอยู่ใกล้เส้นตรง = residuals แจกแจงแบบปกติ

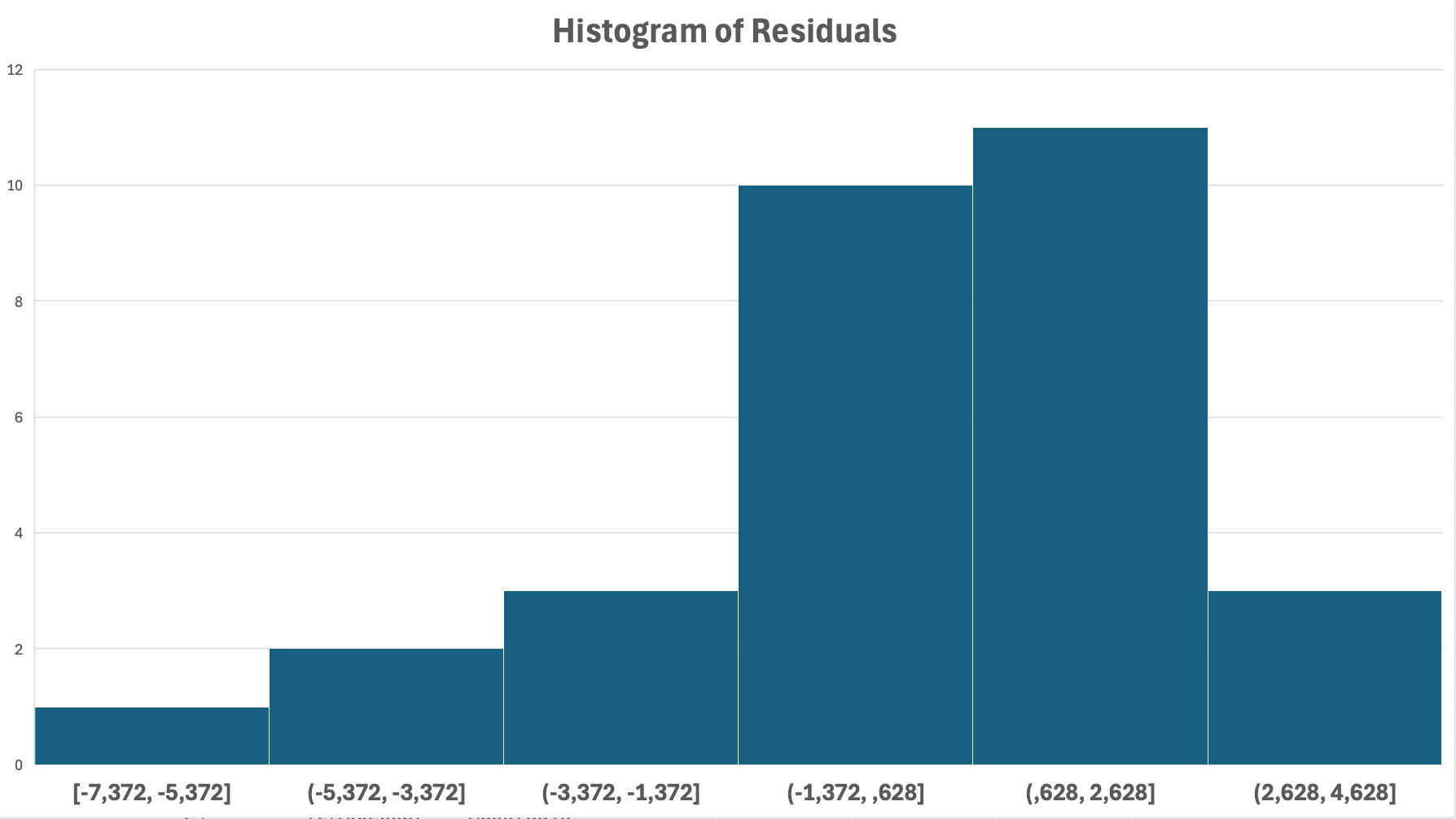
กราฟ histogram ของ residuals ใน Excel สำหรับ simple linear regression แสดงการกระจายแบบปกติ (bell-shaped distribution) ซึ่งบ่งบอกว่า residuals ตรงตามสมมติฐานการแจกแจงแบบปกติสำหรับการวิเคราะห์ regression

รูปที่ 14: การตรวจสอบ normality - histogram ของ residuals แสดงรูปร่างคล้ายกระดิ่ง (bell-shaped) บ่งบอกการแจกแจงแบบปกติ

อะไรที่ต้องมองหา:

Histogram มีรูปร่างคล้ายกระดิ่ง (bell-shaped)
Normal probability plot มีจุดข้อมูลอยู่ใกล้เส้นตรง
Histogram เบ้ (skewed) มาก หรือมี outliers เยอะ = ละเมิด assumption

ถ้าละเมิด assumption:

ลองใช้ data transformation (log, square root)
ลบ outliers ที่มีปัญหา (ถ้าสมเหตุสมผล)
ใช้ bootstrap methods หรือ robust regression

4. Homoscedasticity (ความแปรปรวนคงที่)

Assumption: Residuals ต้องมีความแปรปรวนคงที่ทุกระดับของ X

วิธีตรวจสอบใน Excel:

จาก regression output คัดลอกคอลัมน์ Predicted Values และ Residuals
สร้าง scatter plot ของ Predicted Values (แกน X) vs. Residuals (แกน Y)

อะไรที่ต้องมองหา:

จุดข้อมูลกระจายตัวสม่ำเสมอรอบเส้น y = 0 (random scatter)
ถ้าเห็นรูปแบบ funnel shape (กรวย) หรือ spreading pattern = heteroscedasticity (ละเมิด assumption)

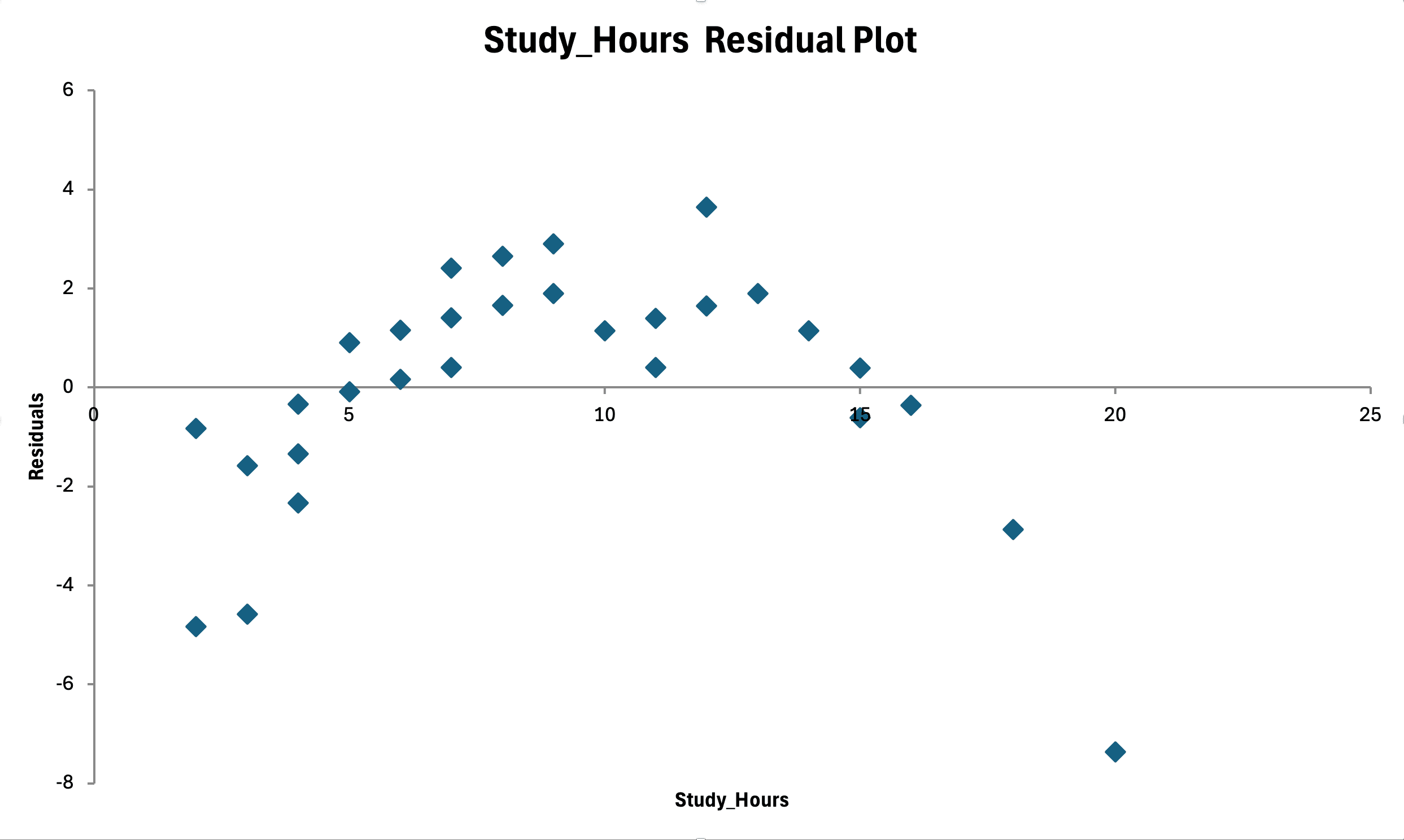
กราฟ scatter plot ของ residuals เทียบกับค่าที่ทำนายใน Excel สำหรับ simple linear regression แสดงความแปรปรวนคงที่ (homoscedasticity) ตลอดช่วงโดยไม่มีรูปแบบกรวยที่บ่งบอก heteroscedasticity

รูปที่ 15: การตรวจสอบ homoscedasticity - residuals เทียบกับค่าที่ทำนายแสดงการกระจายแบบสุ่มโดยไม่มีรูปแบบกรวย (ความแปรปรวนคงที่)

ถ้าละเมิด assumption:

ใช้ data transformation (log, square root)
ใช้ weighted least squares regression
ใช้ robust standard errors

อ่านเพิ่มเติม: Homoscedasticity Assumption คืออะไร

การรายงานการตรวจสอบ Assumptions ในวิทยานิพนธ์

ในบทระเบียบวิธีวิจัย (Methods section):

"ก่อนการวิเคราะห์ regression ได้ตรวจสอบ scatter plots เพื่อยืนยันความเป็นเส้นตรงระหว่างชั่วโมงการศึกษาและคะแนนสอบ มีการตรวจสอบ residual plots และ histograms เพื่อเช็ค homoscedasticity และ normality ของ residuals สมมติฐานทั้งหมดเป็นไปตามเกณฑ์ สนับสนุนการใช้ simple linear regression"

ถ้า assumptions ถูกละเมิด:

"การตรวจสอบ residual plots ด้วยสายตาพบ heteroscedasticity (รูปแบบกรวย) เพื่อแก้ไขการละเมิดนี้ ตัวแปรตามถูกแปลงด้วย log transformation ซึ่งช่วยปรับปรุงการกระจายตัวของ residuals การวิเคราะห์ regression ทำกับคะแนนสอบที่แปลงด้วย log แล้ว"

การรายงานผลลัพธ์ Simple Linear Regression แบบ APA Format

เมื่อคุณเขียนวิทยานิพนธ์หรือบทความวิชาการ คุณต้องรายงานผลลัพธ์ regression ตามรูปแบบ APA (American Psychological Association) นะ

รูปแบบการรายงานแบบ APA

ตัวอย่าง APA Format:

ทำการวิเคราะห์ simple linear regression เพื่อศึกษาความสัมพันธ์ระหว่างชั่วโมงการศึกษาและคะแนนสอบ โมเดล regression มีนัยสำคัญทางสถิติ F(1, 18) = 45.23, p < .001 และอธิบายความแปรปรวนของคะแนนสอบได้ 71.5% (R² = .715) ชั่วโมงการศึกษาทำนายคะแนนสอบได้อย่างมีนัยสำคัญ b = 8.52, t(18) = 6.73, p < .001, 95% CI [5.89, 11.15]

องค์ประกอบสำคัญที่ต้องรายงาน

Model Significance: รายงาน F-statistic, degrees of freedom, และ p-value
- ตัวอย่าง: F(1, 18) = 45.23, p < .001
R-squared: รายงานเปอร์เซ็นต์ของ variance ที่อธิบายได้
- ตัวอย่าง: R² = .715 (71.5%)
Coefficient: รายงาน unstandardized coefficient (b), t-statistic, p-value, และ 95% CI
- ตัวอย่าง: b = 8.52, t(18) = 6.73, p < .001, 95% CI [5.89, 11.15]

ตัวอย่างประโยครายงานผลแบบภาษาไทย

การวิเคราะห์การถดถอยเชิงเส้นอย่างง่าย (simple linear regression) แสดงให้เห็นว่าชั่วโมงการศึกษาสามารถทำนายคะแนนสอบได้อย่างมีนัยสำคัญทางสถิติ (F(1, 18) = 45.23, p < .001) โดยอธิบายความแปรปรวนของคะแนนสอบได้ร้อยละ 71.5 (R² = .715) เมื่อชั่วโมงการศึกษาเพิ่มขึ้น 1 ชั่วโมง คะแนนสอบจะเพิ่มขึ้น 8.52 คะแนนโดยเฉลี่ย (b = 8.52, t(18) = 6.73, p < .001, 95% CI [5.89, 11.15])

ตารางรายงานผลลัพธ์แบบ APA

นอกจากรายงานด้วยข้อความแล้ว คุณควรใส่ตารางด้วยนะ:

ตัวแปร	B	SE	β	t	p	95% CI
Intercept	47.33	1.85	—	25.58	< .001	[43.54, 51.12]
ชั่วโมงอ่านหนังสือ	2.75	0.09	.98	29.16	< .001	[2.56, 2.95]

ตารางที่ 7: Simple Linear Regression ทำนายคะแนนสอบจากชั่วโมงอ่านหนังสือ

หมายเหตุ. n = 30. R² = .97, F(1, 28) = 850.27, p < .001. B = unstandardized regression coefficient. SE = standard error. β = standardized coefficient. CI = confidence interval.

รายการตรวจสอบการรายงาน

เมื่อรายงาน regression ในวิทยานิพนธ์ ให้รวมองค์ประกอบเหล่านี้ทั้งหมดนะ:

ในเนื้อหา (ย่อหน้าผลการวิจัย):

ประเภทการวิเคราะห์ ("ทำการวิเคราะห์ simple linear regression...")
คำถามวิจัย/สมมติฐานที่ทดสอบ
คำกล่าวเกี่ยวกับการตรวจสอบสมมติฐาน
นัยสำคัญของโมเดลโดยรวม: F(df_regression, df_residual) = ค่า F, ค่า p
R² พร้อมการตีความ ("อธิบายความแปรปรวนได้ X%")
สมการ regression: Y = a + bX
การตีความ coefficient พร้อมทิศทางและขนาด
นัยสำคัญของ coefficient: β = ค่า, t(df) = ค่า t, ค่า p
ช่วงความเชื่อมั่น 95% สำหรับ coefficient

ในตาราง:

หมายเลขตารางและชื่อตารางเป็นตัวเอียง
Unstandardized coefficients (B)
Standard errors (SE)
Standardized coefficients (β) ถ้าเกี่ยวข้อง
สถิติ t และค่า p
ช่วงความเชื่อมั่น 95%
หมายเหตุตารางพร้อม n, R², สถิติ F

ข้อผิดพลาดที่พบบ่อยเมื่อทำ Simple Linear Regression ใน Excel

มาดูข้อผิดพลาดทั่วไปที่นักศึกษาและนักวิจัยมักเจอเมื่อทำ regression analysis ใน Excel และวิธีหลีกเลี่ยงนะ

1. ลืมตรวจสอบ Assumptions

ข้อผิดพลาด: รัน regression แล้วก็รายงานผลลัพธ์ทันที โดยไม่ได้ตรวจสอบว่าข้อมูลเป็นไปตาม assumptions ของ linear regression

ทำไมถึงเป็นปัญหา: ถ้าข้อมูลละเมิด assumptions (เช่น ไม่ linear, มี heteroscedasticity) ผลลัพธ์ของคุณอาจไม่ถูกต้องหรือทำนายผิดพลาดได้

วิธีแก้ไข:

เช็ค linearity ด้วย scatter plot
เช็ค normality ด้วย histogram ของ residuals
เช็ค homoscedasticity ด้วย residual plot
ใช้เวลาตรวจสอบ assumptions ก่อน ที่จะไว้ใจผลลัพธ์

2. เลือก X และ Y Range ผิด

ข้อผิดพลาด: เลือกคอลัมน์ผิดสำหรับ X และ Y หรือรวมหัวคอลัมน์ (headers) เข้าไปด้วย

ทำไมถึงเป็นปัญหา: Excel จะคำนวณ regression ด้วยข้อมูลผิด ทำให้ได้ผลลัพธ์ที่ไม่ถูกต้อง

วิธีแก้ไข:

ตรวจสอบให้แน่ใจว่าคุณเลือก ข้อมูลเฉพาะตัวเลข (ไม่ใช่ headers)
ใช้ตัวเลือก Labels ใน Regression dialog ถ้าคุณรวม headers ไว้
ตรวจสอบอีกครั้งว่าคุณใส่ตัวแปรถูก: Input Y Range = ตัวแปรตาม, Input X Range = ตัวแปรอิสระ

3. แปลความหมาย R-squared ผิด

ข้อผิดพลาด: คิดว่า R² สูง = โมเดลดีเสมอ หรือ R² ต่ำ = โมเดลแย่เสมอ

ทำไมถึงเป็นปัญหา: R² บอกเพียงว่าโมเดลอธิบายความแปรปรวนได้เท่าไหร่ แต่ไม่ได้บอกว่าโมเดลมีความหมายทางทฤษฎีหรือทำนายได้ดีนะ

วิธีแก้ไข:

พิจารณา R² ร่วมกับ context ของสาขาวิชาของคุณ
ใน social sciences, R² = 0.30-0.50 ก็ถือว่าพอใช้ได้
ให้ความสำคัญกับ theoretical meaning และ practical significance มากกว่าแค่ตัวเลข R²

4. ใช้ Regression กับข้อมูลที่มี Outliers โดยไม่ได้จัดการ

ข้อผิดพลาด: รัน regression ทันทีโดยไม่ได้เช็ค outliers ก่อน

ทำไมถึงเป็นปัญหา: Outliers สามารถบิดเบือน regression line ได้มาก ทำให้ได้ผลลัพธ์ที่ไม่สะท้อนรูปแบบข้อมูลส่วนใหญ่

วิธีแก้ไข:

สร้าง scatter plot ก่อนรัน regression เพื่อเช็ค outliers
พิจารณาลบ outliers (ถ้าเป็น data entry errors หรือมีเหตุผลสมควร)
ใช้ robust regression methods ถ้าไม่สามารถลบ outliers ได้

5. สรุปว่ามี Causation จาก Correlation

ข้อผิดพลาด: สรุปว่า X ทำให้เกิด Y เพียงเพราะพบว่า X ทำนาย Y ได้อย่างมีนัยสำคัญทางสถิติ

ทำไมถึงเป็นปัญหา: Regression แสดงเพียง association (ความสัมพันธ์) ไม่ใช่ causation (เหตุผล) นะ

ตัวอย่าง: การพบว่าการดื่มกาแฟสัมพันธ์กับผลการทำงานที่ดีขึ้นไม่ได้หมายความว่ากาแฟทำให้ทำงานดีขึ้น อาจมีตัวแปรที่สาม (เช่น แรงจูงใจ) ที่มีผลต่อทั้งสองตัวแปร

วิธีแก้ไข:

ใช้ภาษาที่ระมัดระวัง: "X predicted Y" ไม่ใช่ "X caused Y"
พิจารณาตัวแปรที่สาม (confounding variables) ที่อาจมีผล
ใช้ experimental designs ถ้าคุณต้องการสรุปเรื่อง causation

6. ลืม Check Significance ของโมเดลและ Coefficients

ข้อผิดพลาด: รายงานผลลัพธ์ regression โดยไม่ได้เช็คว่าโมเดลและ coefficients มีนัยสำคัญทางสถิติหรือไม่

ทำไมถึงเป็นปัญหา: โมเดลที่ไม่มีนัยสำคัญทางสถิติ (Significance F ≥ 0.05) หมายความว่าผลลัพธ์อาจเกิดจากความบังเอิญได้

วิธีแก้ไข:

เช็ค Significance F ก่อนเสมอ (ควร < 0.05)
เช็ค p-value ของแต่ละ coefficient ด้วย
รายงานเฉพาะผลลัพธ์ที่มีนัยสำคัญทางสถิติเท่านั้น

7. ใช้ Simple Linear Regression เมื่อควรใช้ Multiple Regression

ข้อผิดพลาด: ใช้เพียง 1 predictor เมื่อมีตัวแปรหลายตัวที่มีผลต่อ outcome

ทำไมถึงเป็นปัญหา: การละเลย important predictors อาจทำให้เกิด omitted variable bias และได้ผลลัพธ์ที่ไม่ถูกต้อง

วิธีแก้ไข:

ถ้าคุณมีตัวแปรอิสระหลายตัว ให้ใช้ multiple linear regression แทน
พิจารณาทฤษฎีและงานวิจัยก่อนหน้าว่ามีตัวแปรอื่นๆ ที่ควรรวมไว้หรือไม่

ข้อจำกัดของการทำ Simple Linear Regression ใน Excel

แม้ว่า Excel จะเป็นเครื่องมือที่ดีสำหรับ basic regression analysis แต่ก็มีข้อจำกัดบางอย่างที่คุณควรรู้นะ

ข้อจำกัดของ Excel

ประเภท Regression	ทำอะไร	Excel ทำได้ไหม	โปรแกรมทางเลือก
Logistic Regression	ทำนายผลลัพธ์แบบไบนารี (ใช่/ไม่ใช่, ผ่าน/ไม่ผ่าน, 0/1)	ไม่ได้	SPSS (Binary Logistic), R (glm function)
Multinomial Logistic	ทำนายผลลัพธ์เชิงกลุ่ม (3+ กลุ่มที่ไม่มีลำดับ)	ไม่ได้	SPSS (Multinomial Logistic), R (multinom)
Ordinal Regression	ทำนายผลลัพธ์เชิงกลุ่มที่มีลำดับ (ต่ำ/กลาง/สูง)	ไม่ได้	SPSS (Ordinal Regression), R (polr)
Stepwise Regression	เลือกตัวแปรอัตโนมัติตามเกณฑ์	ไม่ได้	SPSS (Linear Regression with Stepwise), R (step function)
Hierarchical Regression	เพิ่มตัวทำนายเป็นบล็อกตามทฤษฎี	ไม่ได้ (ทำ manual ได้)	SPSS (Hierarchical blocks), R (manual comparison)
Moderation Analysis	ทดสอบว่าผลของ X ต่อ Y ขึ้นกับตัวแปรกำกับ M หรือไม่	ไม่ได้	SPSS with PROCESS Macro, R (interactions)
Mediation Analysis	ทดสอบว่า X มีผลต่อ Y ผ่านตัวแปรคั่นกลาง M หรือไม่	ไม่ได้	SPSS with PROCESS Macro, R (lavaan, mediation)
Polynomial Regression	ใส่เส้นโค้ง quadratic, cubic (เทอม X², X³)	ได้ (เพิ่มคอลัมน์ X² เอง)	SPSS, R (syntax ง่ายกว่า)
Simple Linear Regression	ทำนาย Y จาก X ต่อเนื่องตัวเดียว	ได้	SPSS, R (ก็มีเหมือนกัน)
Multiple Linear Regression	ทำนาย Y จากตัวทำนาย 2+ ตัว	ได้	SPSS, R (ก็มีเหมือนกัน)

ตารางที่ 8: ความสามารถของ Excel Regression เทียบกับความต้องการ Software สถิติ

สิ่งที่ Excel คำนวณไม่ได้:

VIF (Variance Inflation Factor): ตรวจจับ multicollinearity ใน multiple regression
Durbin-Watson Statistic: ทดสอบ autocorrelation ในข้อมูล time series
Cook's Distance: ระบุ outliers ที่มีอิทธิพล
DFBETAS: วัดอิทธิพลต่อ coefficients แต่ละตัว
Leverage values: ระบุจุดที่มี leverage สูง
Standardized Residuals: ตรวจจับ outliers ง่ายกว่า raw residuals

วิธีแก้ไข:

สำหรับ simple regression, multicollinearity ไม่ใช่ปัญหา (มีตัวทำนายเดียว)
คำนวณ standardized residuals เอง: (Residual / Standard Error)
ใช้ SPSS/R ถ้าอาจารย์ที่ปรึกษาต้องการ diagnostics ขั้นสูง

เมื่อไหร่ควรใช้ Software อื่น

แม้ว่า Excel จะเหมาะสำหรับ simple linear regression พื้นฐาน แต่คุณควรพิจารณาใช้ software อื่นเมื่อ:

คุณมีตัวแปรอิสระหลายตัว (ใช้ SPSS หรือ R สำหรับ multiple regression)
คุณต้องการ advanced diagnostics เช่น multicollinearity checks, Cook's distance, etc.
คุณต้องการทำ hierarchical regression, moderated regression, หรือ mediation analysis
ข้อมูลของคุณมีขนาดใหญ่มาก (> 50,000 rows)
คุณต้องการ automate analysis หรือสร้าง reproducible reports

แนะนำ:

สำหรับการเรียนรู้และ quick analyses: Excel
สำหรับวิทยานิพนธ์และงานวิจัยเผยแพร่: SPSS, R, หรือ Python
สำหรับ advanced statistical modeling: R หรือ Python

คำถามที่พบบ่อย (FAQ)

Next Steps: นำ Regression ไปใช้กับงานวิจัยวิทยานิพนธ์ของคุณ

ตอนนี้คุณมีกรอบการทำงานที่สมบูรณ์สำหรับการทำ simple linear regression ใน Excel แล้ว ตั้งแต่การเตรียมข้อมูล การตรวจสอบ assumptions ไปจนถึงการรายงานผลแบบ APA กุญแจสำคัญของความสำเร็จในวิทยานิพนธ์ไม่ใช่แค่การรัน analysis แต่คือการเข้าใจว่าเมื่อไหร่ควรใช้ วิธีแปลความหมายผลลัพธ์อย่างถูกต้อง และวิธีสื่อสารผลการวิจัยอย่างชัดเจนต่อคณะกรรมการสอบ

ก่อนที่คุณจะทำ regression analysis ขั้นสุดท้าย:

ตรวจสอบ assumptions โดยใช้ diagnostic plots ที่อธิบายไว้ในคู่มือนี้ อย่าข้ามขั้นตอนการตรวจสอบ assumptions นะ—คณะกรรมการสอบจะถามคุณเกี่ยวกับเรื่องนี้ระหว่างการสอบป้องกัน
เช็คข้อจำกัดของ Excel เทียบกับความต้องการของงานวิจัยคุณ ถ้าคณะกรรมการคาดหวัง logistic regression, stepwise selection, หรือ moderation/mediation analysis คุณจะต้องใช้ SPSS หรือ R แทน
เขียนร่างบท Methods ที่อธิบายแนวทางการวิเคราะห์ของคุณ การทดสอบ assumptions และรูปแบบการรายงานแบบ APA ก่อนที่จะรัน analyses ขั้นสุดท้าย
คำนวณและรายงาน effect sizes นอกเหนือจากแค่ p-values R² เล่าเรื่องของ practical significance ที่ p-values ทำไม่ได้
ผสมผสานกับ analyses อื่นๆ ตามความจำเป็น Regression มักทำงานควบคู่กับ สถิติเชิงพรรณนา, t-tests, หรือ ANOVA ในบทผลการวิจัยที่ครอบคลุม

อย่าลืมว่า regression แสดงความสัมพันธ์และการทำนาย ไม่ใช่เหตุผล (causation) นะ ความแข็งแกร่งของข้อสรุปของคุณขึ้นอยู่กับการออกแบบการวิจัย (experimental vs observational), ขนาดตัวอย่าง, การปฏิบัติตาม assumptions, และเหตุผลทางทฤษฎี

เมื่อคุณพร้อมที่จะวิเคราะห์ตัวแปรทำนายหลายตัวพร้อมกัน ให้ก้าวไปสู่ multiple linear regression สำหรับการจัดการข้อมูลที่ไม่สมบูรณ์ก่อนทำ regression ให้ดูวิธีจัดการข้อมูลหาย (Missing Data) ใน Excel สำหรับงานวิจัยที่ใช้แบบสอบถาม ให้แน่ใจว่าคุณได้วิเคราะห์ข้อมูลแบบสอบถามอย่างถูกต้องก่อนที่จะใช้เทคนิค regression

References

American Psychological Association. (2020). Publication manual of the American Psychological Association (7th ed.). https://doi.org/10.1037/0000165-000

Cohen, J. (1988). Statistical power analysis for the behavioral sciences (2nd ed.). Lawrence Erlbaum Associates.

Green, S. B. (1991). How many subjects does it take to do a regression analysis? Multivariate Behavioral Research, 26(3), 499–510. https://doi.org/10.1207/s15327906mbr2603_7