วิธีวิเคราะห์ข้อมูลแบบสอบถามใน Excel: คู่มือฉบับสมบูรณ์สำหรับวิทยานิพนธ์และงานวิจัย

•By Natcharee Chaisirijirasin•th
Statistical TestsExcelResearch Methods

หลังจากที่คุณเก็บข้อมูลจากแบบสอบถามสำหรับวิทยานิพนธ์เสร็จแล้ว สิ่งที่ต้องทำต่อไปคือนำข้อมูลเหล่านี้มาวิเคราะห์ใน Excel อย่างเป็นระบบ ขั้นตอนนี้หลายคนมักรู้สึกว่ายากเพราะต้องจัดการกับตัวเลขเชิงสถิติเยอะ

ข่าวดีก็คือ Excel มันเป็นเครื่องมือที่ทรงพลังเพียงพอสำหรับการวิเคราะห์ข้อมูลแบบสอบถามอย่างถูกต้องตามหลักวิชาการ โดยไม่ต้องใช้โปรแกรมทางสถิติที่แพงอย่าง SPSS ด้วยวิธีการที่เหมาะสม คุณสามารถคำนวณความเชื่อมั่น วิเคราะห์สถิติเชิงพรรณนา ทดสอบสมมติฐาน และจัดรูปแบบผลลัพธ์ตามมาตรฐานวิชาการสำหรับวิทยานิพนธ์ได้เลย

บทความนี้จะพาคุณไปดูกระบวนการวิเคราะห์ข้อมูลแบบสอบถามใน Excel อย่างครบถ้วน คุณจะได้เรียนรู้วิธีเตรียมข้อมูล เช็คความเชื่อมั่นด้วย Cronbach's Alpha คำนวณสถิติเชิงพรรณนา เลือกสถิติทดสอบที่เหมาะสม และเขียนผลการวิจัยในรูปแบบ APA โดยจะอธิบายแบบทีละขั้นตอนตั้งแต่การจัดการข้อมูลดิบจากแบบสอบถามจนถึงการนำเสนอผลในรูปแบบที่เหมาะสมสำหรับวิทยานิพนธ์

สิ่งที่คุณจะได้เรียนรู้ในบทความนี้:

  • วิธีจัดระเบียบและเช็คความถูกต้องของข้อมูลแบบสอบถามก่อนวิเคราะห์
  • คำนวณ Cronbach's Alpha เพื่อดูความเชื่อมั่นของมาตรวัด
  • คำนวณสถิติเชิงพรรณนาสำหรับข้อมูล Likert scale
  • เลือกและใช้สถิติทดสอบที่เหมาะสม
  • สร้างตารางแจกแจงความถี่และตารางไขว้
  • เขียนผลการวิจัยเชิงสถิติในรูปแบบ APA

คุณสามารถศึกษาควบคู่กับการลงมือทำได้เลยโดยดาวน์โหลด Survey Analysis Excel Template จากส่วนดาวน์โหลดใน sidebar

การวิเคราะห์ข้อมูลแบบสอบถามคืออะไร?

การวิเคราะห์ข้อมูลแบบสอบถามก็คือกระบวนการแปลงคำตอบจากแบบสอบถามให้กลายเป็นข้อมูลที่มีความหมาย เพื่อใช้ตอบคำถามวิจัยของคุณ สำหรับนักศึกษาที่กำลังทำวิทยานิพนธ์ กระบวนการนี้มักจะรวมถึงการคำนวณค่าความเชื่อมั่น สรุปรูปแบบของคำตอบ และทดสอบสมมติฐานเกี่ยวกับความสัมพันธ์ระหว่างตัวแปร

แบบสอบถามทางวิชาการส่วนใหญ่จะใช้ Likert scale ซึ่งผู้ตอบจะให้คะแนนความเห็นด้วยกับข้อความตั้งแต่ 1 (ไม่เห็นด้วยอย่างยิ่ง) ถึง 5 (เห็นด้วยอย่างยิ่ง) คำตอบเหล่านี้ต้องจัดการแบบเฉพาะเจาะจง เพราะทางเทคนิคแล้วมันเป็นข้อมูลระดับ ordinal แต่นักวิจัยมักจะใช้งานเหมือนกับข้อมูลระดับ interval เพื่อวัตถุประสงค์ทางสถิติ

แล้วคุณจะวิเคราะห์อย่างไรขึ้นอยู่กับว่าคุณอยากรู้อะไร:

เป้าหมายการวิจัยวิธีการวิเคราะห์
อธิบายรูปแบบของคำตอบความถี่, ค่าเฉลี่ย, ส่วนเบี่ยงเบนมาตรฐาน
ตรวจสอบคุณภาพแบบสอบถามความเชื่อมั่น Cronbach's Alpha
เปรียบเทียบสองกลุ่มIndependent samples t-test
เปรียบเทียบหลายกลุ่มOne-way ANOVA
ศึกษาความสัมพันธ์Pearson correlation
ทำนายผลลัพธ์Regression analysis

เป้าหมายการวิจัยทั่วไปและวิธีการวิเคราะห์ทางสถิติที่เหมาะสม

ก่อนที่จะเริ่มคำนวณอะไร คุณต้องมีข้อมูลที่จัดโครงสร้างให้เรียบร้อยก่อน ส่วนถัดไปจะบอกวิธีเตรียมข้อมูลแบบสอบถามสำหรับการวิเคราะห์

การเตรียมข้อมูลแบบสอบถามสำหรับการวิเคราะห์

การจัดระเบียบและเช็คความถูกต้องของข้อมูลเป็นขั้นตอนแรกที่สำคัญมาก เพราะจะช่วยป้องกันปัญหาตอนวิเคราะห์

การจัดโครงสร้างข้อมูล

ตาราง Excel สำหรับการวิจัยควรมีโครงสร้างง่ายๆ ก็คือ แต่ละแถวคือผู้ตอบ 1 คน และแต่ละคอลัมน์คือ 1 คำถามหรือตัวแปร แถวแรกใส่ชื่อคอลัมน์ที่สั้นและเข้าใจง่าย

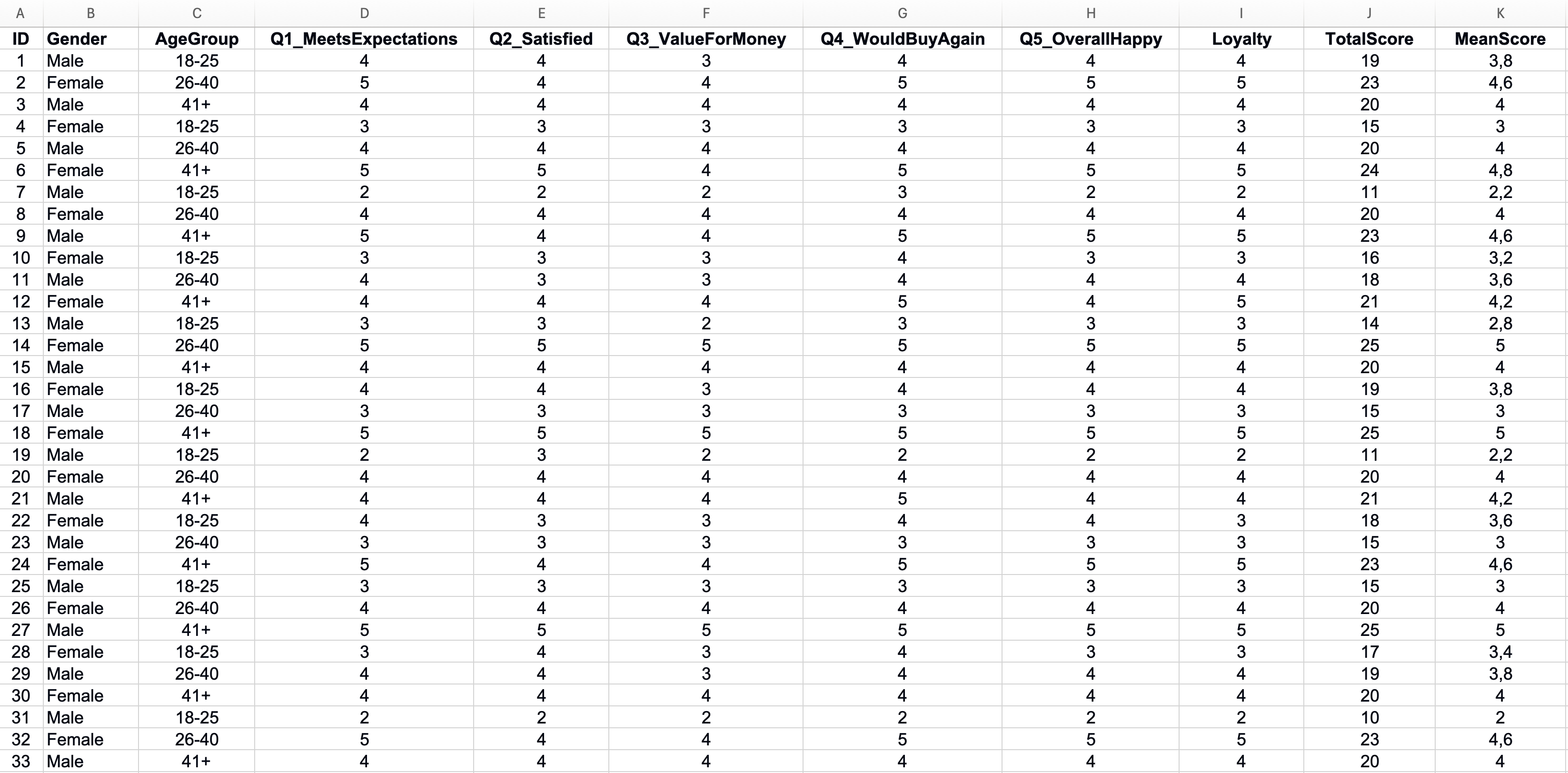Properly organized Excel survey data with headers in row 1 showing ID and Gender and Age and Q1-Q5 and TotalScore columns and numeric responses in rows 2-31 รูปที่ 1: โครงสร้างข้อมูลสำรวจใน Excel ที่จัดระเบียบอย่างเหมาะสม

หมายเหตุ: ชุดข้อมูลตัวอย่างและตัวอย่างทั้งหมดในคู่มือนี้จะใช้ชื่อคอลัมน์เป็นภาษาอังกฤษ (อย่างเช่น Gender, AgeGroup, Q1_MeetsExpectations, Loyalty) เพื่อให้เป็นไปตามมาตรฐานการวิจัยระดับสากลและเพื่อความเข้ากันได้กับซอฟต์แวร์ทางสถิติ ชื่อตัวแปรเหล่านี้จะถูกระบุในวงเล็บตลอดคู่มือ

กฎบางข้อที่จะทำให้ข้อมูลของคุณพร้อมสำหรับการวิเคราะห์:

  • ใช้รหัสตัวเลขสำหรับคำตอบ (1-5 สำหรับ Likert scale, 1 สำหรับใช่และ 0 สำหรับไม่ใช่)
  • เก็บ 1 ตัวแปรต่อ 1 คอลัมน์
  • ไม่ merge cell หรือเพิ่มแถวว่างระหว่างข้อมูล
  • ใช้การ coding ที่เหมือนกันตลอด (ไม่ผสมระหว่างมาตรวัด 1-5 กับ 0-4)

หมายเหตุสำหรับผู้ใช้ Excel นอกสหรัฐอเมริกา: ตัวคั่นในสูตร Excel จะขึ้นอยู่กับการตั้งค่าภูมิภาคของคุณ ถ้าระบบของคุณใช้จุลภาคเป็นตัวคั่นทศนิยม (เช่น 3,14 แทน 3.14) คุณต้องใช้เครื่องหมายอัฒภาค (;) แทนจุลภาคในสูตร ตัวอย่างเช่น ใช้ =COUNTIF(B2:B101;1) แทน =COUNTIF(B2:B101,1) สูตรทั้งหมดในคู่มือนี้ใช้รูปแบบสหรัฐอเมริกา (จุลภาค) ลองปรับให้เข้ากับการตั้งค่าภูมิภาคของคุณนะ

การ Coding ตัวแปรเชิงกลุ่ม

คำตอบจากแบบสอบถามมักจะมีข้อมูลเชิงกลุ่มเช่น เพศ (Gender), กลุ่มอายุ (AgeGroup), ระดับการศึกษา หรือแผนก ลองแปลงคำตอบที่เป็นข้อความให้เป็นรหัสตัวเลขก่อนวิเคราะห์

คำตอบเดิมรหัสตัวเลข
ชาย1
หญิง2
ไม่ระบุ3

ตัวอย่างการ coding ตัวแปรเชิงกลุ่มสำหรับคำตอบเพศ

ลองสร้าง sheet แยกในไฟล์ Excel สำหรับเก็บ coding scheme ที่บันทึกความหมายของแต่ละตัวเลข เอกสารอ้างอิงนี้จะมีประโยชน์มากตอนตีความผลและเขียนบทที่ 3

การจัดการข้อคำถามที่ต้อง Reverse Score

แบบสอบถามบางชุดจะมีข้อคำถามที่ใช้คำในเชิงลบเพื่อเช็คว่าผู้ตอบตั้งใจตอบจริงๆ หรือเปล่า ก่อนคำนวณคะแนนรวมของมาตรวัด คุณต้อง reverse-code ข้อเหล่านี้เพื่อให้คำตอบทั้งหมดหันไปทางเดียวกัน

สำหรับ Likert scale 5 ระดับ สูตรการ reverse score คือ:

Reversed Score=(Max Scale Value+1)−Original Score\text{Reversed Score} = (\text{Max Scale Value} + 1) - \text{Original Score}

ใน Excel ถ้าค่าสูงสุดของมาตรวัดคือ 5 และคำตอบเดิมอยู่ในเซลล์ B2:

=6-B2

คำตอบ 1 จะกลายเป็น 5, คำตอบ 2 จะกลายเป็น 4 แบบนี้ไปเรื่อยๆ ลองสร้างคอลัมน์ใหม่สำหรับข้อที่ reverse แล้ว อย่าไปเขียนทับข้อมูลเดิมนะ

การระบุข้อมูลที่ขาดหาย

คำตอบที่ขาดหายมันสร้างปัญหาให้กับการวิเคราะห์ทางสถิติ ก่อนจะทำอะไรต่อ ลองเช็คก่อนว่ามีช่องว่างอยู่ตรงไหนบ้างในชุดข้อมูล

ใช้ฟังก์ชัน COUNTBLANK ของ Excel เพื่อนับเซลล์ว่างในแต่ละคอลัมน์:

=COUNTBLANK(B2:B101)

มันจะบอกคุณว่ามีผู้ตอบกี่คนที่ข้ามคำถามนั้น ค่าที่ขาดหายเล็กน้อยเป็นเรื่องปกติ แต่ถ้าคำถามไหนมีคำตอบขาดหายเยอะกว่าข้ออื่นมาก ลองเช็คดูว่าทำไม บางทีคำถามนั้นอาจจะสับสนหรือเป็นเรื่องละเอียดอ่อน

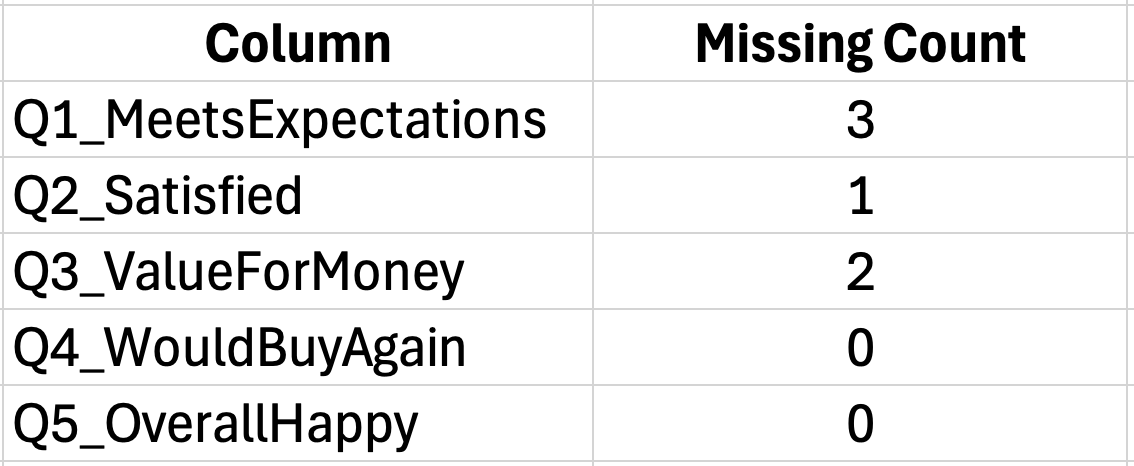Excel COUNTBLANK results showing blank counts for each survey column with Q4 highlighted showing 5 missing values compared to 0-1 for other questions รูปที่ 2: การระบุข้อมูลที่ขาดหายไปด้วยฟังก์ชัน COUNTBLANK

พอเจอข้อมูลที่ขาดหายนิดหน่อย คุณมีทางเลือก:

  • ลบ case ที่มีค่าขาดหายออกไป (listwise deletion)
  • แทนที่ค่าที่ขาดหายด้วยค่าเฉลี่ยของข้อนั้น (mean imputation)
  • ปล่อยไว้แล้วให้ Excel ไม่นับเซลล์ว่างตอนคำนวณ

อาจารย์ส่วนใหญ่จะรับ listwise deletion เมื่อคำตอบที่ขาดหายน้อยกว่า 5% อย่าลืมบันทึกวิธีที่คุณใช้ไว้ในบทที่ 3 นะ

การคำนวณคะแนนรวมและคะแนนรายมิติ

เครื่องมือวัดจากแบบสอบถามมักจะมีหลาย subscale ที่วัดสิ่งต่างๆ กัน ก่อนวิเคราะห์ ให้คำนวณคะแนนรวมสำหรับแต่ละ subscale โดยการรวม (หรือหาค่าเฉลี่ย) ข้อที่เกี่ยวข้อง

สำหรับมาตรวัด "ความพึงพอใจของลูกค้า" 5 ข้อ:

=SUM(B2:F2)

สูตรนี้จะคำนวณคะแนนรวมสำหรับผู้ตอบคนที่ 1 จากข้อในคอลัมน์ B ถึง F แล้วคัดลอกลงมาสำหรับผู้ตอบทุกคน

การใช้ AVERAGE แทน SUM จะทำให้คะแนนอยู่บนมาตรวัดเดิม 1-5 ซึ่งง่ายต่อการตีความกว่า:

=AVERAGE(B2:F2)

Excel showing columns B-F with individual Likert items Q1-Q5 and column G with SUM formula for Satisfaction_Total and column H with AVERAGE formula for Satisfaction_Mean รูปที่ 3: การคำนวณคะแนนรวมและคะแนนเฉลี่ยสำหรับ subscales

พอข้อมูลพร้อมแล้ว คุณก็สามารถตรวจสอบได้ว่ามาตรวัดของคุณวัดสิ่งที่ต้องการวัดได้อย่างน่าเชื่อถือหรือเปล่า

การเช็คความเชื่อมั่น: Cronbach's Alpha ใน Excel

ก่อนจะวิเคราะห์ผลแบบสอบถาม คุณต้องยืนยันก่อนว่าแบบสอบถามของคุณใช้งานได้จริง Cronbach's Alpha จะบอกคุณว่าข้อต่างๆ ในมาตรวัดวัด construct เดียวกันอย่างสม่ำเสมอหรือเปล่า มาตรวัดที่ความเชื่อมั่นต่ำจะให้ผลลัพธ์ที่ไม่น่าเชื่อถือ

หลักการคิดแบบนี้: ถ้าคุณวัดคนเดียวกันสองครั้งด้วยมาตรวัดที่ดี คุณควรจะได้คะแนนที่ใกล้เคียงกัน มาตรวัดที่ไม่ดีจะให้ผลต่างกันทุกครั้ง ทำให้ไม่สามารถสรุปอะไรได้

เมื่อไหร่ควรคำนวณ Cronbach's Alpha

ลองคำนวณความเชื่อมั่นสำหรับมาตรวัดที่มีหลายข้อในแบบสอบถาม ถ้าคุณใช้เครื่องมือที่มีคนพัฒนาไว้แล้วอย่าง Job Satisfaction Scale หรือ Customer Loyalty Index นักวิจัยก่อนหน้าก็เคยพิสูจน์ความเชื่อมั่นแล้ว แต่คุณควรคำนวณ Alpha สำหรับกลุ่มตัวอย่างของคุณเองด้วย เพื่อยืนยันว่ามาตรวัดใช้ได้ในบริบทของคุณ

คุณต้องการ Cronbach's Alpha เมื่อ:

  • แบบสอบถามมีหลายข้อที่วัด construct เดียว
  • คุณวางแผนจะรวมหรือหาค่าเฉลี่ยข้อต่างๆ เป็นคะแนนมาตรวัด
  • คุณต้องพิสูจน์ว่าเครื่องมือของคุณน่าเชื่อถือ

ไม่ต้องการมันสำหรับ:

  • มาตรวัดข้อเดียว (1 คำถามต่อ 1 construct)
  • คำถามข้อมูลประชากร
  • คำถามข้อเท็จจริงที่มีคำตอบชัดเจน

สูตร Cronbach's Alpha

Cronbach's Alpha มีค่าตั้งแต่ 0 ถึง 1 ยิ่งค่าสูงก็ยิ่งบ่งบอกว่าข้อต่างๆ สอดคล้องกันดี สูตรคือ:

α=KK−1×(1−∑i=1Kσi2σT2)\alpha = \frac{K}{K-1} \times \left(1 - \frac{\sum_{i=1}^{K} \sigma_{i}^{2}}{\sigma_{T}^{2}}\right)

โดยที่:

  • K = จำนวนข้อในมาตรวัด
  • σ²ᵢ = ความแปรปรวนของแต่ละข้อ
  • σ²ₜ = ความแปรปรวนของคะแนนรวม

แม้ว่าสูตรจะดูซับซ้อน แต่ Excel สามารถจัดการได้แบบไม่ยาก

การคำนวณทีละขั้นตอนใน Excel

ลองดูตัวอย่างการวิเคราะห์กับมาตรวัดความพึงพอใจของลูกค้า 5 ข้อ โดยใช้คำตอบจากผู้ตอบ 30 คน

ขั้นตอนที่ 1: คำนวณความแปรปรวนของแต่ละข้อ

ใช้ฟังก์ชัน VAR.S สำหรับความแปรปรวนของกลุ่มตัวอย่าง ถ้าคำตอบของข้อแรกอยู่ในคอลัมน์ B (แถว 2-31):

=VAR.S(B2:B31)

ทำซ้ำสำหรับแต่ละคอลัมน์ของข้อคำถาม วางการคำนวณความแปรปรวนเหล่านี้ไว้ในพื้นที่สรุปด้านล่างข้อมูล

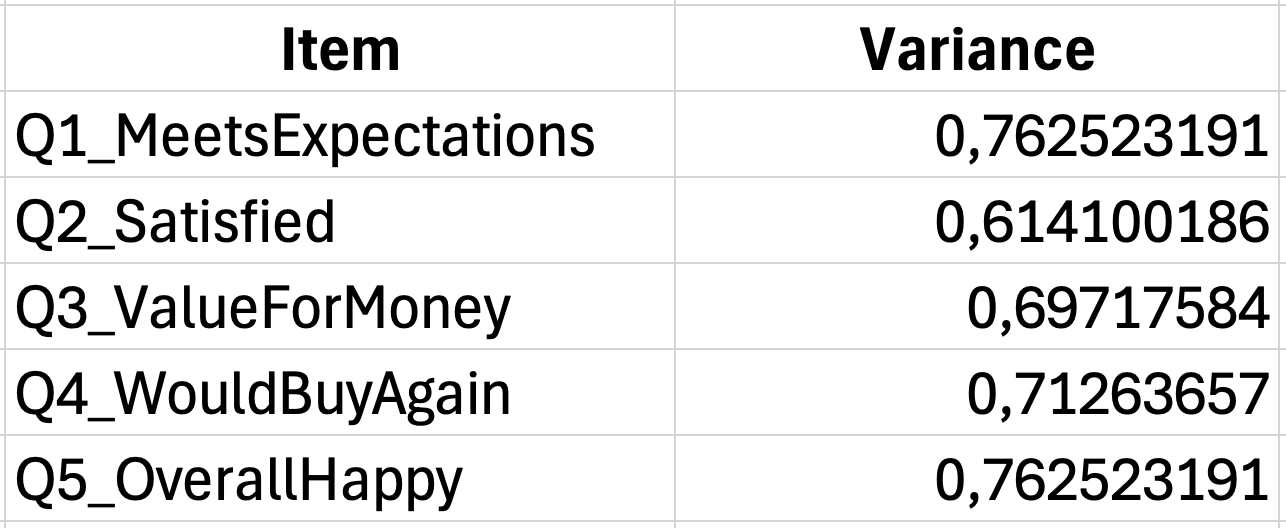Excel showing variance calculations for 5 items in summary section with Item 1 Variance is 1.24, Item 2 is 0.98, Item 3 is 1.15, Item 4 is 1.08, Item 5 is 1.32, with VAR.S formula visible in formula bar รูปที่ 4: การคำนวณความแปรปรวนของแต่ละข้อคำถาม

ขั้นตอนที่ 2: รวมความแปรปรวนของข้อทั้งหมด

รวมความแปรปรวนของแต่ละข้อเข้าด้วยกัน:

=SUM(G35:G39)

ถ้าความแปรปรวนของข้อต่างๆ อยู่ในเซลล์ G35 ถึง G39 สูตรนี้จะให้ผลรวมของความแปรปรวนทั้งหมด

ขั้นตอนที่ 3: คำนวณความแปรปรวนของคะแนนรวม

ก่อนอื่น ค ำนวณคะแนนรวมของผู้ตอบแต่ละคนโดยรวมข้อต่างๆ:

=SUM(B2:F2)

แล้วคำนวณความแปรปรวนของคะแนนรวมเหล่านี้:

=VAR.S(G2:G31)

ขั้นตอนที่ 4: ใช้สูตร Cronbach's Alpha

เมื่อ K = 5 ข้อ, ผลรวมความแปรปรวนของข้ออยู่ในเซลล์ G40 และความแปรปรวนรวมอยู่ในเซลล์ G42:

=(5/4)*(1-(G40/G42))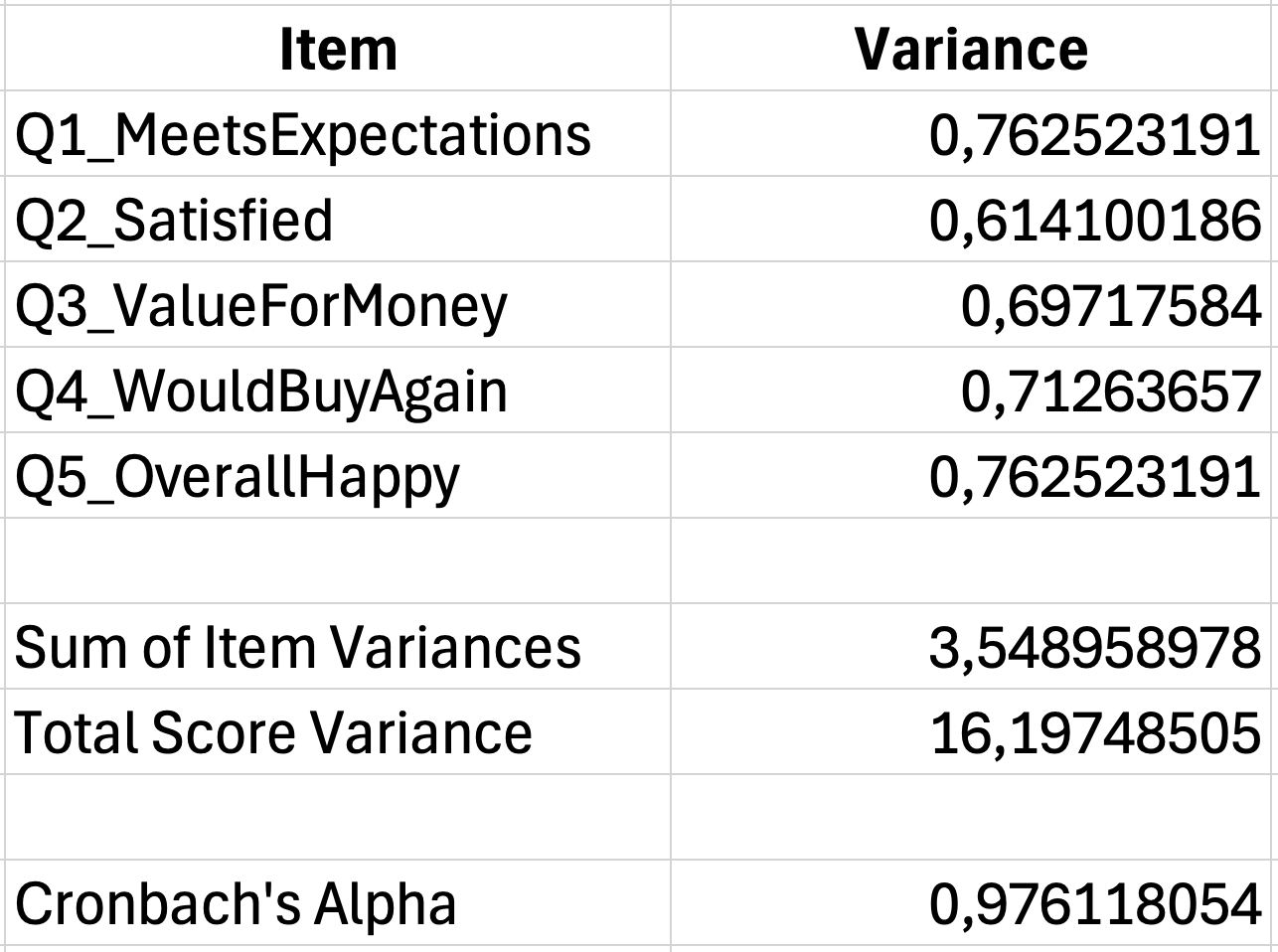

Excel showing complete Cronbach's Alpha calculation with individual item variances and sum of variances and total score column and total score variance and final Alpha formula showing result of 0.78 รูปที่ 5: การคำนวณ Cronbach's Alpha แบบสมบูรณ์ (α = 0.78)

การตีความค่า Alpha

พอคุณได้ค่าสัมประสิทธิ์แล้ว ใช้ตารางนี้ตีความผลลัพธ์:

ค่า Alphaการตีความ
0.90 ขึ้นไปดีเยี่ยม
0.80 ถึง 0.89ดี
0.70 ถึง 0.79ยอมรับได้
0.60 ถึง 0.69น่าสงสัย
0.50 ถึง 0.59ต่ำ
ต่ำกว่า 0.50ยอมรับไม่ได้

แนวทางการตีความ Cronbach's Alpha สำหรับการประเมินความเชื่อมั่น

สำหรับงานวิจัยวิทยานิพนธ์ มาตรฐานทางวิชาการกำหนดให้มีค่า Alpha 0.70 ขึ้นไป ค่าระหว่าง 0.60 ถึง 0.70 อาจจะโอเคได้สำหรับงานวิจัยเชิงสำรวจหรือมาตรวัดที่มีน้อยกว่า 10 ข้อ (Pallant, 2016)

ถ้าค่า Alpha ของคุณต่ำกว่าระดับที่ยอมรับได้ ลองพิจารณา:

  • ลบข้อที่ไม่สัมพันธ์กับข้ออื่นๆ ออก
  • เช็คข้อที่ต้อง reverse-score ที่คุณอาจจะลืม recode
  • เช็คดูว่า construct นั้นอาจจะมีหลายมิติจริงๆ

การรายงานความเชื่อมั่นในวิทยานิพนธ์

รวมผลการทดสอบความเชื่อมั่นไว้ในบทที่ 3 หรือบทที่ 4 รูปแบบมาตรฐานตาม APA style:

"มาตรวัดความพึงพอใจของลูกค้ามีความสอดคล้องภายในระดับที่ยอมรับได้ (Cronbach's α = 0.78, 5 ข้อ)"

สำหรับหลายมาตรวัด นำเสนอความเชื่อมั่นในรูปแบบตาราง:

มาตรวัดจำนวนข้อCronbach's Alpha
ความพึงพอใจของลูกค้า50.78
ความตั้งใจซื้อ40.84
ความภักดีต่อแบรนด์60.91

ตัวอย่างตารางความเชื่อมั่นแสดงค่า Cronbach's Alpha สำหรับหลายมาตรวัด

สำหรับคำแนะนำโดยละเอียดเกี่ยวกับการคำนวณ Cronbach's Alpha พร้อม template ดาวน์โหลด ดูคู่มือฉบับเต็มของเรา: วิธีคำนวณ Cronbach's Alpha ใน Excel

หากต้องการคู่มือฉบับสมบูรณ์พร้อมตัวอย่างจริง ขั้นตอนแก้ไขปัญหาสำหรับค่า Alpha ที่ต่ำหรือสูง และแบบฟอร์มการรายงานแบบ APA ดูบทความโดยละเอียดของเรา: วิธีแปลผล Cronbach's Alpha

สถิติเชิงพรรณนาสำหรับข้อมูลแบบสอบถาม

พอยืนยันความเชื่อมั่นแล้ว คุณก็สามารถอธิบายได้ว่าข้อมูลของคุณบอกอะไร สถิติเชิงพรรณนาช่วยสรุปรูปแบบของคำตอบและช่วยให้ผู้อ่านเข้าใจกลุ่มตัวอย่างของคุณ ก่อนที่คุณจะนำเสนอสถิติอนุมาน

สำหรับข้อมูลแบบสอบถาม คุณมักจะรายงานความถี่ ค่าเฉลี่ย (mean), มัธยฐาน (median), ฐานนิยม (mode) และส่วนเบี่ยงเบนมาตรฐาน (SD) ว่าจะใช้สถิติอะไรบ้างขึ้นอยู่กับประเภทข้อมูลและคำถามวิจัยของคุณ

การสร้างตารางแจกแจงความถี่

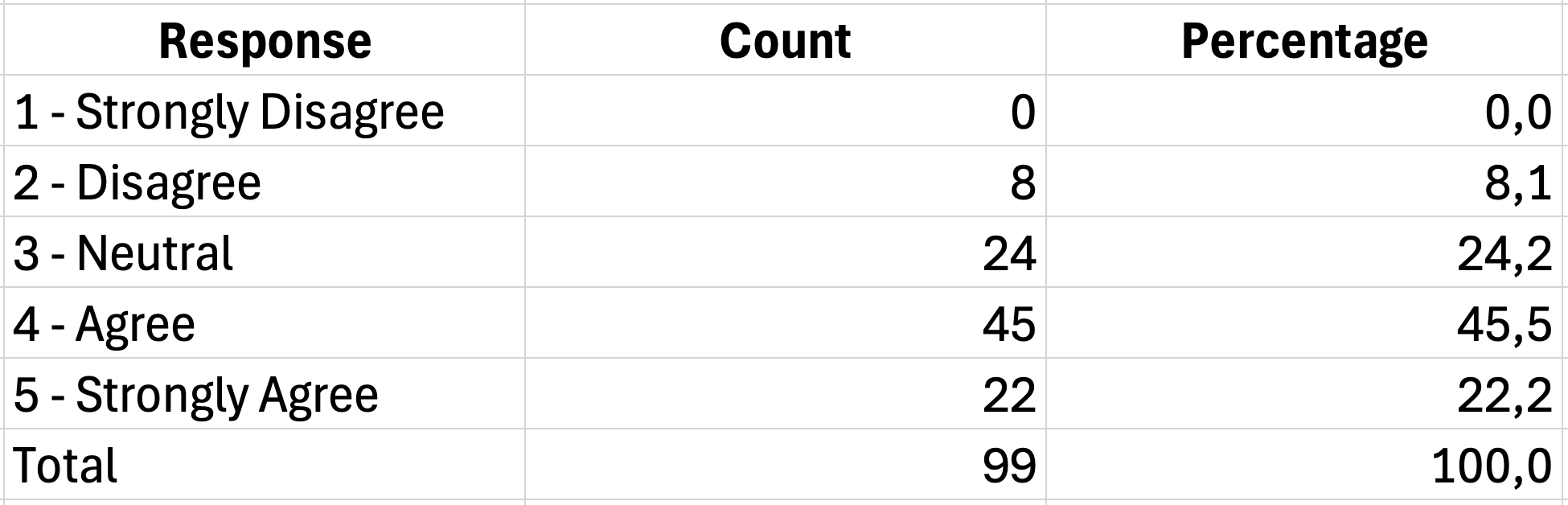
ตารางความถี่จะแสดงว่าคำตอบกระจายตัวอย่างไรในแต่ละตัวเลือก มันช่วยตอบคำถามเช่น "มีผู้ตอบกี่คนที่เห็นด้วยกับข้อความนี้?" หรือ "ผู้เข้าร่วมกี่เปอร์เซ็นต์ที่เลือกแต่ละตัวเลือก?"

ใช้ฟังก์ชัน COUNTIF เพื่อนับคำตอบสำหรับแต่ละตัวเลือก:

=COUNTIF(B2:B101,1)

สูตรนี้จะนับว่ามีผู้ตอบกี่คนที่เลือก "1" (ไม่เห็นด้วยอย่างยิ่ง) ในช่วง B2:B101

Excel showing frequency table construction with raw Likert data on left and summary table on right displaying Response Value and Count and Percentage columns with COUNTIF formula visible รูปที่ 6: การสร้างตารางความถี่ด้วย COUNTIF

ในการคำนวณเปอร์เซ็นต์ ให้หารจำนวนแต่ละค่าด้วยจำนวนคำตอบทั้งหมด:

=D2/SUM($D$2:$D$6)*100

เครื่องหมาย dollar จะล็อคช่วงรวม เพื่อให้คัดลอกสูตรลงมาโดยไม่เปลี่ยนแปลง

ตารางความถี่ที่สมบูรณ์สำหรับข้อ Likert หนึ่งข้อมีลักษณะแบบนี้:

คำตอบความถี่เปอร์เซ็นต์
1 - ไม่เห็นด้วยอย่างยิ่ง55.0%
2 - ไม่เห็นด้วย1212.0%
3 - เฉยๆ2828.0%
4 - เห็นด้วย3535.0%
5 - เห็นด้วยอย่างยิ่ง2020.0%
รวม100100.0%

ตารางแจกแจงความถี่สำหรับข้อคำถาม Likert scale 5 ระดับ

การคำนวณค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐาน

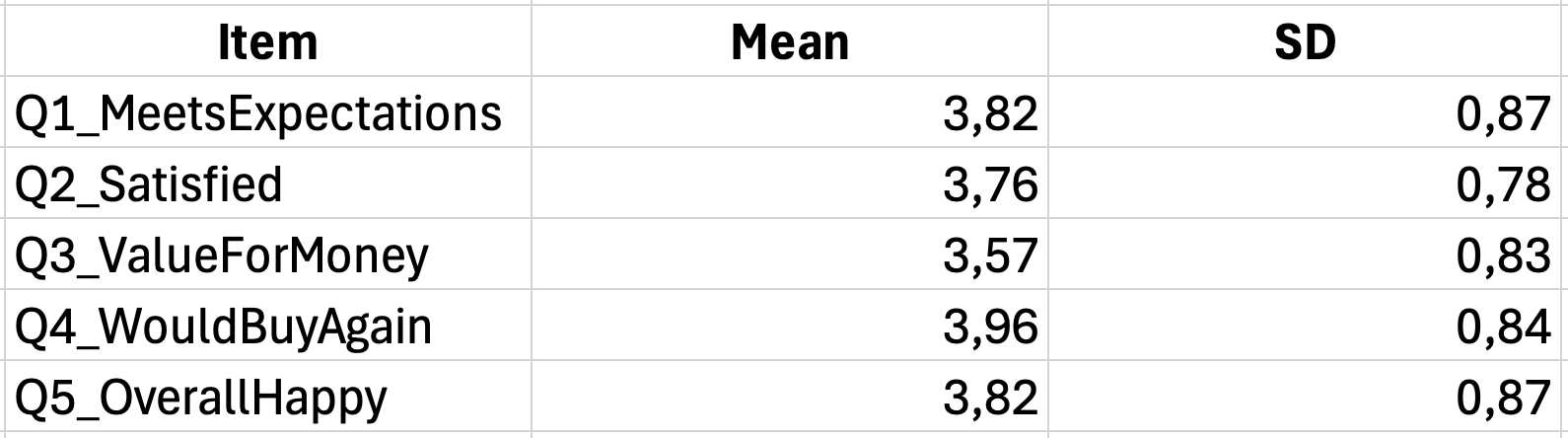
สำหรับข้อมูล Likert scale นักวิจัยมักรายงานค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐาน สถิติเหล่านี้ช่วยสรุปแนวโน้มกลางและการกระจายของคำตอบ

ค่าเฉลี่ยจะบอกว่าคำตอบเฉลี่ยของผู้ตอบทั้งหมดคืออะไร:

=AVERAGE(B2:B101)

ส่วนเบี่ยงเบนมาตรฐานบอกว่าคำตอบแตกต่างจากค่าเฉลี่ยมากน้อยแค่ไหน:

=STDEV.S(B2:B101)

ใช้ STDEV.S (ส่วนเบี่ยงเบนมาตรฐานของกลุ่มตัวอย่าง) แทน STDEV.P เพราะผู้ตอบของคุณเป็นตัวแทนของกลุ่มตัวอย่างจากประชากรที่ใหญ่กว่า

Excel showing mean and SD calculations for multiple survey items in summary table with columns for Item and Mean and SD displaying 5 rows with AVERAGE function visible in formula bar รูปที่ 7: สรุปค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐาน

การสรุปคะแนนมาตรวัด

พอคำนวณคะแนนรวมหรือคะแนนเฉลี่ยสำหรับมาตรวัดแล้ว ให้รายงานสถิติเชิงพรรณนาสำหรับมาตรวัดรวมเหล่านี้ด้วย

สำหรับมาตรวัดความพึงพอใจที่คุณหาค่าเฉลี่ยของข้อ 1-5:

การวัดค่า
ค่าเฉลี่ย3.67
ส่วนเบี่ยงเบนมาตรฐาน0.82
ค่าต่ำสุด1.40
ค่าสูงสุด5.00
พิสัย3.60

สรุปสถิติเชิงพรรณนาสำหรับคะแนนรวมของมาตรวัดความพึงพอใจ

คำนวณโดยใช้:

Mean: =AVERAGE(G2:G101)
SD: =STDEV.S(G2:G101)
Min: =MIN(G2:G101)
Max: =MAX(G2:G101)
Range: =MAX(G2:G101)-MIN(G2:G101)

การตีความค่าเฉลี่ย Likert Scale

คำถามที่พบบ่อยคือ "ค่าเฉลี่ย 3.67 หมายความว่าอะไร?" การตีความก็ขึ้นอยู่กับ anchor ของมาตรวัดของคุณ

สำหรับ Likert scale 5 ระดับมาตรฐานเกี่ยวกับความเห็นด้วย:

ช่วงค่าเฉลี่ยการตีความ
1.00 ถึง 1.80ไม่เห็นด้วยอย่างยิ่ง
1.81 ถึง 2.60ไม่เห็นด้วย
2.61 ถึง 3.40เฉยๆ
3.41 ถึง 4.20เห็นด้วย
4.21 ถึง 5.00เห็นด้วยอย่างยิ่ง

แนวทางการตีความค่าเฉลี่ยบน Likert scale 5 ระดับ

ค่าเฉลี่ยความพึงพอใจ 3.67 อยู่ในช่วง "เห็นด้วย" แสดงว่าผู้ตอบโดยทั่วไปแสดงความพึงพอใจในเชิงบวก

ระวังอย่าตีความความแตกต่างเล็กน้อยมากเกินไปนะ ค่าเฉลี่ย 3.52 เทียบกับ 3.48 อาจจะไม่ได้แตกต่างกันมากพอที่จะมีความหมาย ลองดูส่วนเบี่ยงเบนมาตรฐานและทำการทดสอบทางสถิติก่อนจะบอกว่าความแตกต่างมีนัยสำคัญ

สถิติเชิงพรรณนาแยกตามกลุ่ม

บ่อยครั้งคุณต้องการเปรียบเทียบสถิติระหว่างกลุ่ม เช่น ชายกับหญิง หรือกลุ่มอายุต่างๆ ลองสร้างการคำนวณแยกสำหรับแต่ละกลุ่มย่อย

ฟังก์ชัน AVERAGEIF คำนวณค่าเฉลี่ยสำหรับกลุ่มเฉพาะ:

=AVERAGEIF(A2:A101,"Male",G2:G101)

สูตรนี้จะคำนวณคะแนนความพึงพอใจเฉลี่ยสำหรับผู้ตอบที่ถูก code เป็น "Male" ในคอลัมน์ เพศ (Gender)

Excel showing grouped descriptive statistics comparison table with columns for Group and N and Mean and SD displaying Male and Female rows with AVERAGEIF formula in formula bar รูปที่ 8: สถิติเชิงพรรณนาแยกตามกลุ่มด้วย AVERAGEIF

สำหรับส่วนเบี่ยงเบนมาตรฐานแยกตามกลุ่ม คุณต้องใช้ DSTDEV กับช่วงเกณฑ์ หรือกรองข้อมูลแล้วคำนวณแยกกัน

การจัดรูปแบบสถิติเชิงพรรณนาสำหรับวิทยานิพนธ์

นำเสนอสถิติเชิงพรรณนาในรูปแบบตารางที่อ่านง่าย รูปแบบ APA ต้องการการจัดรูปแบบเฉพาะ:

ตารางที่ 1 สถิติเชิงพรรณนาสำหรับข้อคำถามมาตรวัดความพึงพอใจของลูกค้า

ข้อคำถามMSD
ผลิตภัณฑ์ตรงกับความคาดหวังของฉัน3.820.98
ฉันพึงพอใจกับการซื้อครั้งนี้3.671.05
คุณภาพสมกับราคา3.541.12
ฉันจะซื้อผลิตภัณฑ์นี้อีก3.910.89
โดยรวมแล้ว ฉันมีความสุขกับผลิตภัณฑ์3.780.94
คะแนนรวมมาตรวัด3.740.82

สถิติเชิงพรรณนาสำหรับข้อคำถามมาตรวัดความพึงพอใจของลูกค้า

หมายเหตุ. N = 100 คำตอบวัดด้วย Likert scale 5 ระดับ (1 = ไม่เห็นด้วยอย่างยิ่ง, 5 = เห็นด้วยอย่างยิ่ง)

ประเด็นสำคัญในการจัดรูปแบบ:

  • ใช้ M สำหรับค่าเฉลี่ย และ SD สำหรับส่วนเบี่ยงเบนมาตรฐาน
  • รายงานทศนิยม 2 ตำแหน่งสำหรับค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐาน
  • รวมขนาดกลุ่มตัวอย่างและคำอธิบายมาตรวัดในหมายเหตุ
  • ทำตัวเอียงชื่อตาราง

การวิเคราะห์ข้อมูล Likert Scale

Likert scale ต้องดูแลเป็นพิเศษเพราะมันอยู่ในพื้นที่สีเทาระหว่างข้อมูล ordinal กับ interval การเข้าใจวิธีวิเคราะห์คำตอบเหล่านี้อย่างถูกต้องจะช่วยป้องกันไม่ให้ผลการวิจัยของคุณมีปัญหา

การถกเถียงระหว่าง Ordinal และ Interval

ในทางเทคนิค คำตอบ Likert เป็นข้อมูล ordinal เพราะความแตกต่างระหว่าง "เห็นด้วย" กับ "เห็นด้วยอย่างยิ่ง" อาจจะไม่เท่ากับความแตกต่างระหว่าง "ไม่เห็นด้วย" กับ "เฉยๆ" แต่นักวิจัยมักจะใช้งาน Likert scale 5 และ 7 ระดับเหมือนกับข้อมูล interval เพื่อความสะดวกในทางปฏิบัติ

วิธีการนี้โดยทั่วไปก็ยอมรับได้เมื่อ:

  • มาตรวัดมีอย่างน้อย 5 ระดับ
  • ตัวเลือกคำตอบมีระยะห่างเท่ากัน (1, 2, 3, 4, 5)
  • คุณวิเคราะห์คะแนนรวมของมาตรวัดแทนที่จะเป็นข้อเดี่ยว

พอคุณรวมหรือหาค่าเฉลี่ยหลายข้อ Likert เป็นคะแนนมาตรวัด ผลลัพธ์ก็จะใกล้เคียงข้อมูล interval มากขึ้น และสามารถวิเคราะห์ด้วยสถิติ parametric ได้

การคำนวณค่าเฉลี่ยของ Construct

ตอนที่แบบสอบถามของคุณวัด construct ทางทฤษฎีด้วยหลายข้อ ลองคำนวณคะแนนเฉลี่ยจากข้อเหล่านั้นสำหรับผู้ตอบแต่ละคน มันจะสร้างตัวแปรเดียวที่แทน construct นั้น

ถ้าข้อ Q1 ถึง Q5 (Q1_MeetsExpectations, Q2_Satisfied, Q3_ValueForMoney, Q4_WouldBuyAgain, Q5_OverallHappy) วัด "ความพึงพอใจในงาน":

=AVERAGE(B2:F2)

คัดลอกลงมาสำหรับผู้ตอบทุกคน คอลัมน์ที่ได้จะมีคะแนนความพึงพอใจของแต่ละคนบนมาตรวัดเดิม 1-5

Excel showing individual item columns Q1-Q5 with various Likert values and new column JobSat_Mean with AVERAGE formula calculating to value 3.60 for first respondent รูปที่ 9: การคำนวณคะแนนเฉลี่ยของ construct จากหลายข้อคำถาม

การจัดการกับคำตอบเป็นกลาง

จุดกลางของ Likert scale (มักจะเป็น "เฉยๆ" หรือ "ไม่เห็นด้วยและไม่คัดค้าน") มักได้รับคำตอบเยอะที่สุด คำตอบเป็นกลางจำนวนมากอาจบอกว่า:

  • ผู้ตอบรู้สึกลังเลจริงๆ
  • คำถามสับสนหรือไม่เกี่ยวข้อง
  • ผู้ตอบเลือกตัวเลือกกลางเพราะง่าย (satisficing)

ลองเช็คความถี่ของคำตอบเป็นกลางสำหรับแต่ละข้อ ถ้าคำถามไหนมีคำตอบเป็นกลางเยอะกว่าข้ออื่นอย่างมาก ลองเช็คการใช้คำ

การสร้างตัวแปรแบบจัดกลุ่ม

บางครั้งคุณอาจต้องรวมคำตอบ Likert ให้เป็นหมวดหมู่น้อยลงสำหรับการวิเคราะห์หรือรายงาน ตัวอย่างเช่น การรวม "เห็นด้วย" กับ "เห็นด้วยอย่างยิ่ง" เป็นหมวด "เห็นด้วย" เดียว

ใช้ฟังก์ชัน IF ซ้อนกัน:

=IF(B2<=2,"Disagree",IF(B2=3,"Neutral","Agree"))

สูตรนี้จะ recode คำตอบ 1-2 เป็น "Disagree", 3 เป็น "Neutral" และ 4-5 เป็น "Agree"

มาตรวัดเดิมหมวดหมู่ที่จัดกลุ่ม
1 - ไม่เห็นด้วยอย่างยิ่งไม่เห็นด้วย
2 - ไม่เห็นด้วยไม่เห็นด้วย
3 - เฉยๆเฉยๆ
4 - เห็นด้วยเห็นด้วย
5 - เห็นด้วยอย่างยิ่งเห็นด้วย

ตัวอย่างการรวม Likert scale 5 ระดับเป็น 3 หมวดหมู่

ตัวแปรที่จัดกลุ่มเหมาะสำหรับการนำเสนอผลให้คนอ่านที่ไม่ใช่นักเทคนิค แทนที่จะบอกว่า "ค่าเฉลี่ยคือ 3.67" คุณสามารถบอกว่า "55% ของผู้ตอบเห็นด้วยหรือเห็นด้วยอย่างยิ่ง"

ความผิดพลาดที่พบบ่อยกับข้อมูล Likert

มีความผิดพลาดหลายข้อที่มักเจอในงานวิทยานิพนธ์ที่เกี่ยวกับ Likert scale:

ความผิดพลาดที่ 1: วิเคราะห์ข้อเดี่ยวด้วยสถิติ parametric

การทำ t-test กับข้อ Likert เดี่ยวนั้นผิดข้อสมมติเรื่องการวัดระดับ interval ลองใช้สถิติ non-parametric แทน (Mann-Whitney U) หรือวิเคราะห์คะแนนรวมของมาตรวัด

ความผิดพลาดที่ 2: ลืม reverse-code ข้อเชิงลบ

ถ้ามาตรวัดของคุณมีข้อที่ใช้คำเชิงลบ พอไม่ reverse-code ก่อนรวม คะแนนมาตรวัดก็จะผิดไปหมด อย่าลืมเช็คแบบสอบถามต้นฉบับว่ามีข้อไหนต้อง reverse-score บ้างนะ

ความผิดพลาดที่ 3: ปฏิบัติกับจุดเป็นกลางเหมือน "ข้อมูลที่ขาดหาย"

นักศึกษาบางคนตัดคำตอบเป็นกลางออกจากการวิเคราะห์ โดยสมมติว่าผู้ตอบเหล่านี้ไม่มีความคิดเห็น มันสร้างอคติได้ เป็นกลางก็เป็นคำตอบที่ถูกต้องที่ควรรวมไว้

ความผิดพลาดที่ 4: ตีความความแตกต่างทศนิยมมากเกินไป

ค่าเฉลี่ย 3.65 ไม่ได้แตกต่างจาก 3.58 อย่างมีความหมายหรอกถ้าไม่มีการทดสอบทางสถิติยืนยัน ลองรายงานขนาดอิทธิพลควบคู่กับค่า p เพื่อกำหนดความสำคัญในทางปฏิบัติ

สำหรับคำแนะนำโดยละเอียดเกี่ยวกับการสร้างและวิเคราะห์มาตรวัด ดูบทความของเราเรื่อง วิธีคำนวณ Cronbach's Alpha ใน Excel ซึ่งจะพาคุณไปดูการวิเคราะห์ข้อและการทดสอบความเชื่อมั่น

การทดสอบสมมติฐานใน Excel

สถิติเชิงพรรณนาบอกคุณว่าเกิดอะไรขึ้นในกลุ่มตัวอย่าง การทดสอบสมมติฐานจะบอกว่าผลที่คุณเจอนี้ใช้ได้กับประชากรที่ใหญ่กว่าหรือเปล่า สถิติทดสอบที่เหมาะสมก็ขึ้นอยู่กับคำถามวิจัย จำนวนกลุ่มที่คุณเปรียบเทียบ และประเภทข้อมูลที่คุณเก็บมา

การเลือกสถิติทดสอบที่เหมาะสม

ลองใช้กรอบการตัดสินใจนี้เพื่อเลือกสถิติทดสอบที่เหมาะสม:

เป้าหมายการวิจัยคืออะไร?เปรียบเทียบค่าเฉลี่ยความสัมพันธ์ความถี่2 กลุ่ม3+ กลุ่มคนกลุ่มเดียวกัน?(ก่อน/หลัง)T-Testแบบจับคู่ใช่T-Testอิสระไม่ใช่ANOVAทางเดียวความแข็งแรง?การทำนาย?สหสัมพันธ์เพียร์สันการถดถอยเชิงเส้นตัวแปรเชิงประเภท?การทดสอบไคสแควร์คำอธิบาย:เริ่มต้น / เป้าหมายวิจัยจุดตัดสินใจการทดสอบทางสถิติ

รูปที่ 10: แผนภูมิการตัดสินใจเพื่อเลือกการทดสอบทางสถิติที่เหมาะสม

คำถามวิจัยจำนวนกลุ่มสถิติทดสอบ
มีความแตกต่างระหว่างค่าเฉลี่ยของสองกลุ่มหรือไม่?2 กลุ่มอิสระIndependent t-test
คะแนนเปลี่ยนแปลงจากก่อนทดสอบถึงหลังทดสอบหรือไม่?2 การวัดที่เกี่ยวข้องกันPaired t-test
มีความแตกต่างระหว่างหลายกลุ่มหรือไม่?3 กลุ่มขึ้นไปOne-way ANOVA
มีความสัมพันธ์ระหว่างสองตัวแปรหรือไม่?ไม่เกี่ยวข้องPearson correlation
ตัวแปรหนึ่งสามารถทำนายอีกตัวหนึ่งได้หรือไม่?ไม่เกี่ยวข้องLinear regression

กรอบการตัดสินใจสำหรับการเลือกสถิติทดสอบที่เหมาะสมตามคำถามวิจัย

ก่อนทำการทดสอบอะไร ลองเช็คก่อนว่าข้อมูลของคุณตรงตามข้อสมมติหรือเปล่า สถิติ parametric ส่วนใหญ่ต้องการให้ข้อมูลกระจายตัวแบบปกติและความแปรปรวนเท่ากัน ถ้ากลุ่มตัวอย่างเล็กหรือข้อมูลไม่ปกติ ลองใช้สถิติ non-parametric แทนนะ

การทำ T-Test ใน Excel

T-test เปรียบเทียบค่าเฉลี่ยระหว่างสองกลุ่ม Excel มีฟีเจอร์นี้ผ่าน Data Analysis Toolpak

การเปิดใช้งาน Data Analysis Toolpak:

  1. คลิก File แล้วเลือก Options
  2. เลือก Add-ins จากเมนูด้านซ้าย
  3. ที่ด้านล่าง เลือก Excel Add-ins แล้วคลิก Go
  4. เลือก Analysis ToolPak แล้วคลิก OK

พอทำเสร็จ ตัวเลือก Data Analysis จะปรากฏในแท็บ Data สำหรับคำแนะนำโดยละเอียดพร้อมภาพหน้าจอ ดูคู่มือของเรา: วิธีเปิดใช้งาน Data Analysis ใน Excel

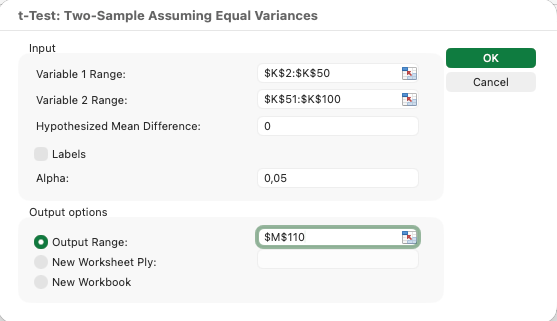
การทำ Independent Samples T-Test:

สมมติว่าคุณต้องการเปรียบเทียบคะแนนความพึงพอใจระหว่างผู้ตอบชายและหญิง

  1. คลิก Data แล้วเลือก Data Analysis
  2. เลือก t-Test: Two-Sample Assuming Equal Variances
  3. สำหรับ Variable 1 Range ให้เลือกคะแนนความพึงพอใจของเพศชาย
  4. สำหรับ Variable 2 Range ให้เลือกคะแนนความพึงพอใจของเพศหญิง
  5. ตั้งค่า Alpha เป็น 0.05
  6. เลือกตำแหน่ง output แล้วคลิก OK

Excel Data Analysis dialog box with t-Test selected showing input fields filled with sample data ranges and alpha set to 0.05 and output options visible รูปที่ 11: การตั้งค่า independent samples t-test

การตีความผลลัพธ์ T-Test:

Excel จะสร้างตารางที่มีสถิติหลายค่า ลองดูที่ค่าสำคัญเหล่านี้:

ค่า Outputความหมาย
Meanคะแนนเฉลี่ยของแต่ละกลุ่ม
Varianceการกระจายของคะแนนภายในแต่ละกลุ่ม
t Statค่า t ที่คำนวณได้
P(T less than or equal to t) two-tailค่า p สำหรับการทดสอบสองหาง
t Critical two-tailค่า t เกณฑ์สำหรับนัยสำคัญ

ค่า output สำคัญจากการวิเคราะห์ t-test ใน Excel และความหมาย

ถ้าค่า p น้อยกว่า 0.05 แสดงว่าความแตกต่างระหว่างกลุ่มมีนัยสำคัญทางสถิติ ถ้าค่า p เกิน 0.05 ก็ไม่สามารถสรุปได้ว่ากลุ่มแตกต่างกัน

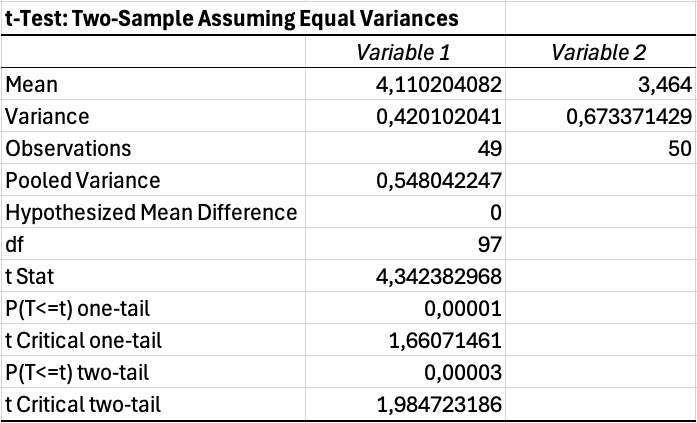Excel t-test output table highlighting key values including Mean for each group showing 3.52 vs 3.78 and t Stat showing -2.14 and P two-tail showing 0.035 with annotation pointing to p-value รูปที่ 12: ผลลัพธ์ t-test แสดงความแตกต่างอย่างมีนัยสำคัญ (p = 0.035)

สำหรับบทเรียน t-test ฉบับเต็มพร้อมคำแนะนำทีละขั้นตอน ดูคู่มือของเรา: T-Test ใน Excel: คู่มือฉบับสมบูรณ์

การทำ One-Way ANOVA

เมื่อเปรียบเทียบสามกลุ่มขึ้นไป ต้องใช้ ANOVA แทนการทำ t-test หลายครั้ง เพราะการทำ t-test หลายครั้งจะเพิ่มโอกาสได้ผลบวกลวง (Type I error)

ตัวอย่าง: เปรียบเทียบคะแนนความพึงพอใจระหว่างสามกลุ่มอายุ (18-25, 26-40, 41+)

  1. จัดข้อมูลโดยให้แต่ละกลุ่มอยู่ในคอลัมน์แยก
  2. คลิก Data แล้วเลือก Data Analysis
  3. เลือก Anova: Single Factor
  4. เลือกช่วง input ที่ครอบคลุมคอลัมน์กลุ่มทั้งหมด
  5. เลือก Labels ถ้าแถวแรกมีหัวคอลัมน์
  6. ตั้งค่า Alpha เป็น 0.05
  7. คลิก OK

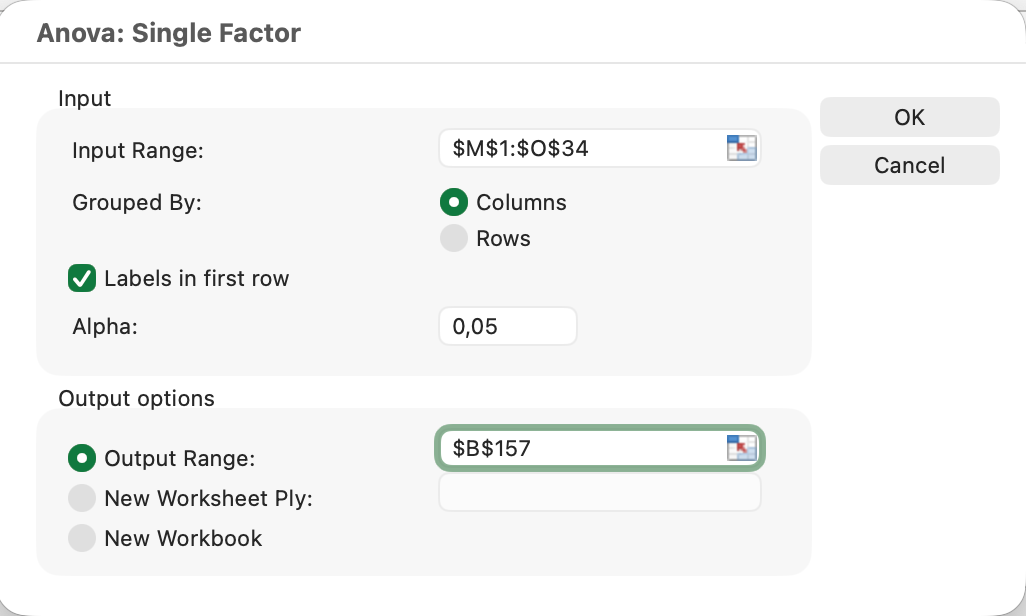Excel showing ANOVA setup with three columns of data labeled Age 18-25 and Age 26-40 and Age 41+ containing satisfaction scores and Anova dialog box with correct settings รูปที่ 13: การตั้งค่า one-way ANOVA สำหรับสามกลุ่มอายุ

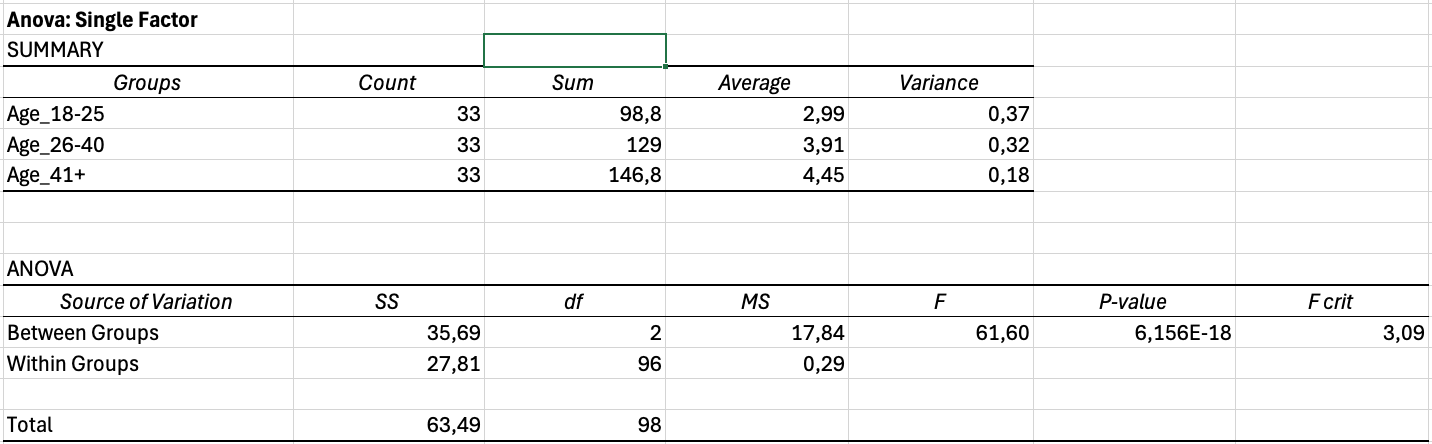Excel ANOVA output table showing F statistic of 61.60 and p-value of 6.156E-18 indicating highly significant differences between age groups รูปที่ 14: ผลลัพธ์ ANOVA แสดงความแตกต่างอย่างมีนัยสำคัญสูง

การตีความผลลัพธ์ ANOVA:

Output จะมีสองตาราง ตาราง Summary แสดงสถิติเชิงพรรณนาสำหรับแต่ละกลุ่ม ตาราง ANOVA แสดงผลการทดสอบ

ค่าสำคัญที่ต้องรายงาน:

SourceSSdfMSFP-value
Between Groups12.4526.224.180.018
Within Groups144.32971.49
Total156.7799

ตัวอย่างตาราง output ANOVA แสดงการแบ่งความแปรปรวนและการทดสอบนัยสำคัญ

ถ้าค่า p น้อยกว่า 0.05 แสดงว่าอย่างน้อยหนึ่งกลุ่มแตกต่างอย่างมีนัยสำคัญจากกลุ่มอื่น แต่ ANOVA ไม่ได้บอกนะว่ากลุ่มไหนแตกต่างกัน ถ้าต้องการรู้ต้องทำ post-hoc tests (ซึ่งต้องการการคำนวณเพิ่มเติมหรือโปรแกรมอื่น)

การคำนวณ Correlation ใน Excel

Correlation วัดความแข็งแกร่งและทิศทางของความสัมพันธ์ระหว่างสองตัวแปรต่อเนื่อง ใช้เมื่อคุณอยากรู้ว่าค่าที่สูงกว่าบนตัวแปรหนึ่งสัมพันธ์กับค่าที่สูงกว่า (หรือต่ำกว่า) บนอีกตัวแปรหนึ่งหรือเปล่า

การใช้ฟังก์ชัน CORREL:

ตัวอย่างเช่น เพื่อหาความสัมพันธ์ระหว่างความพึงพอใจ (Satisfaction_Mean) กับความภักดี (Loyalty):

=CORREL(B2:B101,C2:C101)

สูตรนี้จะคำนวณค่าสัมประสิทธิ์สหสัมพันธ์ Pearson ระหว่างข้อมูลในคอลัมน์ B และ C

การตีความค่าสัมประสิทธิ์สหสัมพันธ์:

ค่าสัมประสิทธิ์อยู่ระหว่าง -1 ถึง +1:

ค่าสัมประสิทธิ์การตีความ
0.90 ถึง 1.00สัมพันธ์ทางบวกแข็งแกร่งมาก
0.70 ถึง 0.89สัมพันธ์ทางบวกแข็งแกร่ง
0.40 ถึง 0.69สัมพันธ์ทางบวกปานกลาง
0.10 ถึง 0.39สัมพันธ์ทางบวกอ่อน
0.00 ถึง 0.09ไม่มีนัยสำคัญ
-0.10 ถึง -0.39สัมพันธ์ทางลบอ่อน
-0.40 ถึง -0.69สัมพันธ์ทางลบปานกลาง
-0.70 ถึง -0.89สัมพันธ์ทางลบแข็งแกร่ง
-0.90 ถึง -1.00สัมพันธ์ทางลบแข็งแกร่งมาก

แนวทางการตีความค่าสัมประสิทธิ์สหสัมพันธ์ Pearson

ค่าสัมประสิทธิ์บวกหมายความว่าตัวแปรเคลื่อนที่ไปด้วยกัน ค่าสัมประสิทธิ์ลบหมายความว่าเคลื่อนที่ในทิศทางตรงข้าม ยิ่งใกล้ 1 หรือ -1 ความสัมพันธ์ยิ่งแข็งแกร่ง

Excel showing correlation calculation with two columns of data for Satisfaction and Loyalty and CORREL formula returning 0.67 and small scatter plot visualizing positive relationship รูปที่ 15: Pearson correlation แสดงความสัมพันธ์เชิงบวกที่แข็งแกร่ง (r = 0.67)

การตรวจสอบนัยสำคัญทางสถิติ:

ฟังก์ชัน CORREL ไม่ให้ค่า p ถ้าต้องการดูว่า correlation มีนัยสำคัญหรือเปล่า ให้เปรียบเทียบกับค่าวิกฤตหรือใช้ Data Analysis Toolpak:

  1. คลิก Data แล้วเลือก Data Analysis
  2. เลือก Correlation
  3. เลือกช่วงข้อมูล
  4. คลิก OK

มันจะสร้าง correlation matrix แต่ยังขาดค่า p สำหรับงานวิทยานิพนธ์ คุณอาจต้องคำนวณค่า p ด้วยตนเองหรือใช้สูตรสำหรับ t-statistic จาก correlation:

t=rn−21−r2t = r \sqrt{\frac{n-2}{1-r^2}}

โดยที่ r คือค่าสัมประสิทธิ์สหสัมพันธ์และ n คือขนาดกลุ่มตัวอย่าง แล้วเปรียบเทียบค่า t นี้กับค่าวิกฤตสำหรับ degrees of freedom (n-2)

สำหรับคู่มือโดยละเอียดรวมถึงการทดสอบนัยสำคัญ ดู: วิธีคำนวณ Pearson Correlation ใน Excel

Cross-Tabulation และการวิเคราะห์ Chi-Square

Cross-tabulation เช็คความสัมพันธ์ระหว่างสองตัวแปรเชิงกลุ่ม มันตอบคำถามเช่น "มีความสัมพันธ์ระหว่างเพศและความชอบผลิตภัณฑ์หรือไม่?" หรือ "กลุ่มอายุต่างๆ เลือกระดับความพึงพอใจต่างกันหรือเปล่า?"

การสร้าง Cross-Tab ด้วย PivotTables

PivotTables เป็นวิธีที่ง่ายที่สุดในการสร้าง cross-tabulation ใน Excel

  1. เลือกข้อมูลรวมทั้งหัวคอลัมน์
  2. คลิก Insert แล้วเลือก PivotTable
  3. เลือกตำแหน่งที่จะวาง PivotTable
  4. ลากตัวแปรหนึ่งไปที่ Rows
  5. ลากตัวแปรอีกตัวไปที่ Columns
  6. ลากตัวแปรใดก็ได้ไปที่ Values (ตั้งค่าเป็น Count)

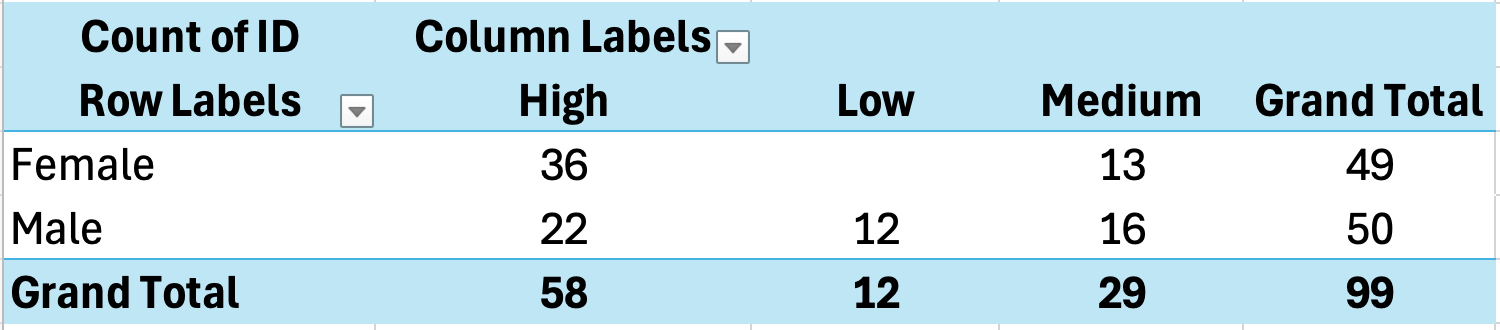Excel PivotTable setup for cross-tabulation showing field list with Gender dragged to Rows and SatisfactionLevel to Columns and Gender to Values displaying Count with resulting frequency table รูปที่ 16: การสร้าง cross-tabulation ด้วย PivotTable

ตัวอย่าง Cross-Tab Output:

ไม่พอใจเฉยๆพอใจรวม
ชาย8152245
หญิง5183255
รวม133354100

Cross-tabulation แสดงความสัมพันธ์ระหว่างเพศและระดับความพึงพอใจ

ถ้าอยากแสดงเปอร์เซ็นต์แทนจำนวน:

  1. คลิกที่ตัวเลขใดๆ ในพื้นที่ Values
  2. คลิกขวาแล้วเลือก Show Values As
  3. เลือก % of Row Total หรือ % of Column Total

การตีความผลลัพธ์ Cross-Tab

Cross-tabulation เผยให้เห็นรูปแบบว่าหมวดหมู่สัมพันธ์กันอย่างไร ในตัวอย่างข้างต้น:

  • 49% ของเพศชายพอใจเทียบกับ 58% ของเพศหญิง
  • เพศชายมีอัตราความไม่พอใจสูงกว่า (18%) เทียบกับเพศหญิง (9%)

แต่ความแตกต่างเชิงพรรณนาเหล่านี้ไม่ได้ยืนยันว่าความสัมพันธ์มีนัยสำคัญทางสถิติ ถ้าต้องการรู้ ต้องใช้ Chi-Square test

Chi-Square Test for Independence

Chi-Square test จะบอกว่าความสัมพันธ์ระหว่างสองตัวแปรเชิงกลุ่มมีนัยสำคัญทางสถิติหรือมีแนวโน้มเกิดจากความบังเอิญ

Excel ไม่มี Chi-Square test ในตัว แต่คุณสามารถคำนวณได้ด้วยสูตร

ขั้นตอนที่ 1: คำนวณความถี่ที่คาดหวัง

สำหรับแต่ละเซลล์ ความถี่ที่คาดหวังคือ:

E=(Row Total)×(Column Total)Grand TotalE = \frac{(\text{Row Total}) \times (\text{Column Total})}{\text{Grand Total}}

สำหรับเซลล์ Male/Dissatisfied: (45 × 13) / 100 = 5.85

ขั้นตอนที่ 2: คำนวณ Chi-Square

χ2=∑(O−E)2E\chi^2 = \sum \frac{(O - E)^2}{E}

โดยที่ O คือความถี่ที่สังเกตได้และ E คือความถี่ที่คาดหวัง

สร้างตารางค่าที่คาดหวัง แล้วคำนวณ chi-square contribution สำหรับแต่ละเซลล์และรวมกัน

ขั้นตอนที่ 3: กำหนดนัยสำคัญ

ใช้ฟังก์ชัน CHISQ.TEST ใน Excel:

=CHISQ.TEST(ObservedRange, ExpectedRange)

สูตรนี้จะคืนค่า p ถ้าน้อยกว่า 0.05 ความสัมพันธ์ก็มีนัยสำคัญ

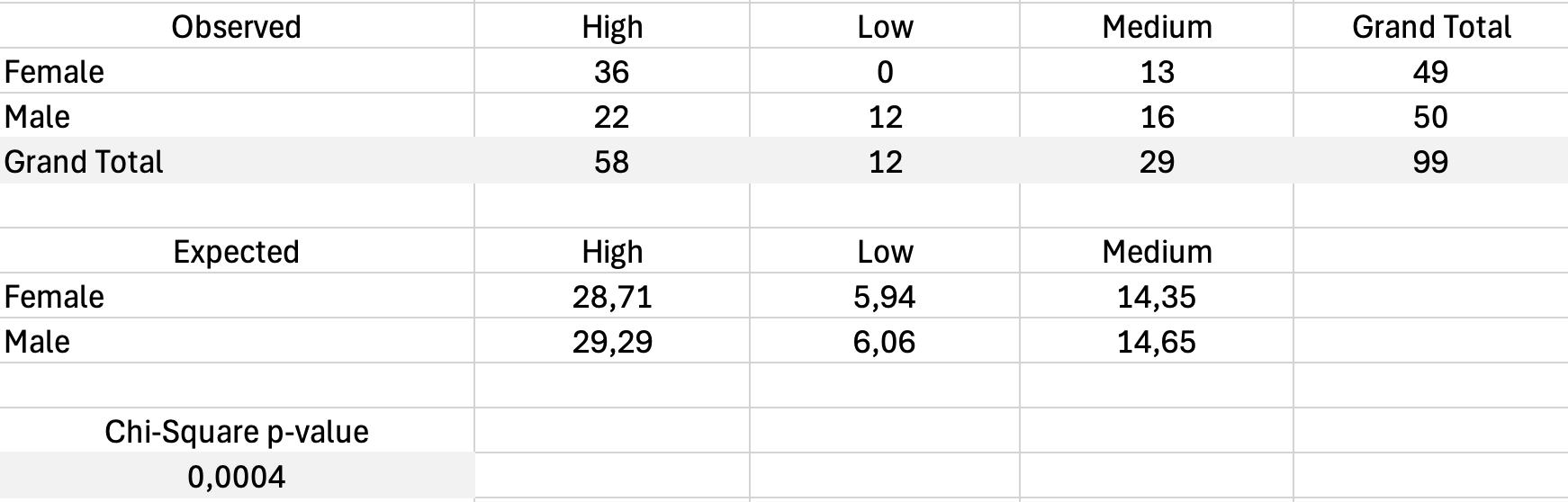Excel showing Chi-Square calculation setup with observed frequencies table and expected frequencies table calculated and CHISQ.TEST formula returning p value 0.042 with annotation indicating significance รูปที่ 17: การคำนวณ Chi-Square test ด้วยความถี่ที่สังเกตและคาดหวัง

การสร้างภาพผลลัพธ์แบบสอบถาม

แผนภูมิแปลงตัวเลขให้เป็นรูปแบบที่ผู้อ่านเข้าใจได้ทันที สำหรับข้อมูลแบบสอบถาม แผนภูมิบางประเภทสื่อสารผลการค้นพบได้ดีกว่าประเภทอื่น

Bar Charts สำหรับความถี่

Bar charts เหมาะที่สุดสำหรับแสดงว่าคำตอบกระจายตัวอย่างไรในแต่ละหมวดหมู่ ใช้สำหรับ:

  • การกระจายตัวของคำตอบ Likert scale
  • การเปรียบเทียบระหว่างกลุ่ม
  • การแยกตามข้อมูลประชากร

สร้าง bar chart จากตารางความถี่:

  1. เลือก label หมวดหมู่และค่าความถี่
  2. คลิก Insert แล้วเลือก Bar Chart หรือ Column Chart
  3. จัดรูปแบบด้วย label ที่ชัดเจนและสีที่เหมาะสม

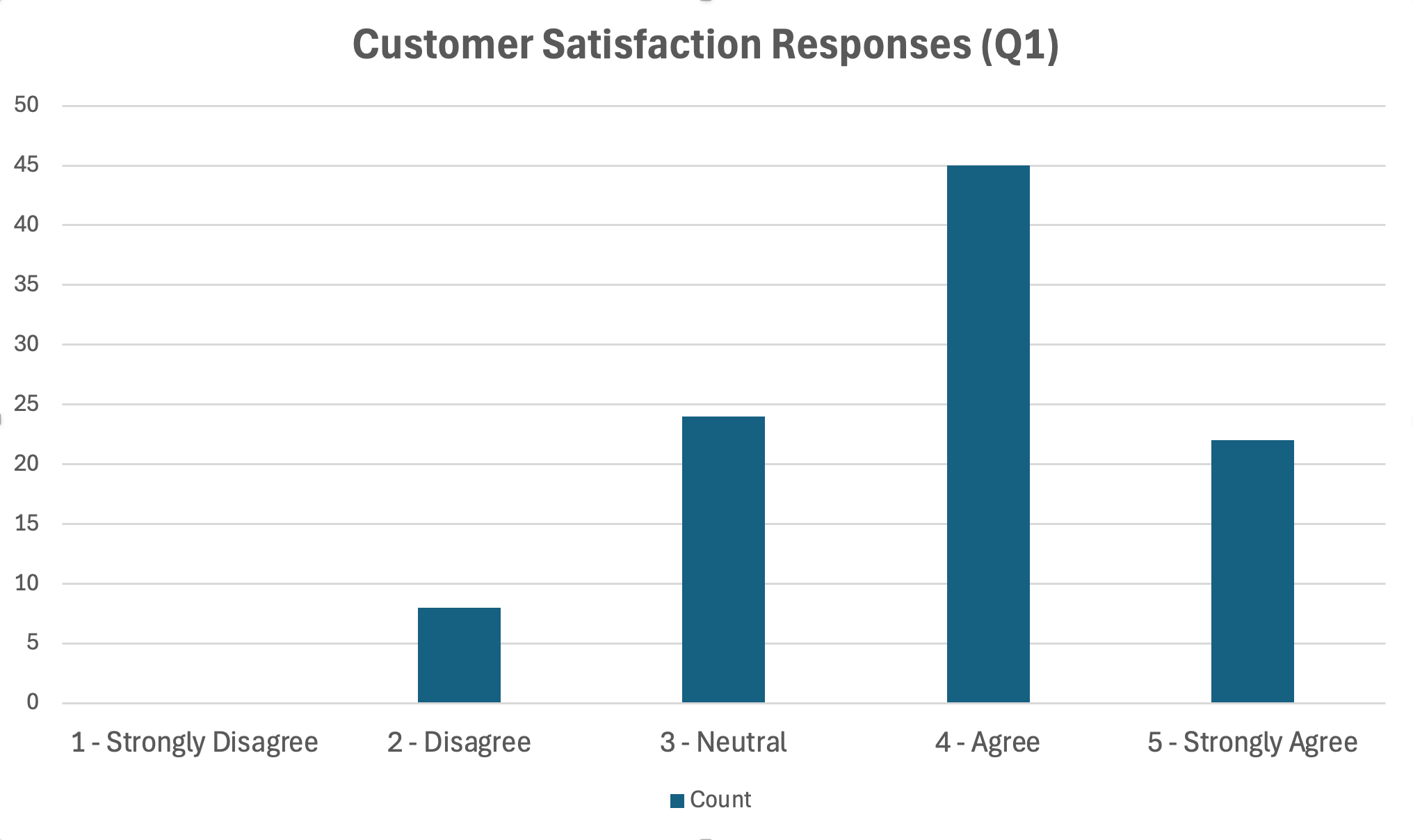Horizontal bar chart showing Likert response distribution with five bars labeled Strongly Disagree through Strongly Agree with data labels showing percentages and title Customer Satisfaction Responses N is 100 รูปที่ 18: กราฟแท่งแสดงการกระจายของคำตอบในมาตรวัด Likert

เคล็ดลับการจัดรูปแบบ:

  • ใช้สีเดียวหรือ gradient (หลีกเลี่ยงสีรุ้ง)
  • เรียงลำดับแท่งอย่างมีเหตุผล (สำหรับ Likert ให้คงลำดับ 1-5)
  • รวม data labels หรือแกนที่ชัดเจนพร้อมค่า
  • เพิ่มขนาดกลุ่มตัวอย่างในชื่อเรื่องหรือหมายเหตุ

การเปรียบเทียบกลุ่มด้วย Clustered Bar Charts

เมื่อเปรียบเทียบคำตอบระหว่างกลุ่ม clustered bar charts วางแท่งเคียงข้างกันเพื่อการเปรียบเทียบที่ง่าย

  1. สร้างตารางสรุปโดยมีกลุ่มเป็นแถวและหมวดหมู่คำตอบเป็นคอลัมน์
  2. เลือกข้อมูลแล้วแทรก Clustered Bar Chart
  3. แต่ละ cluster แทนหนึ่งหมวดหมู่คำตอบพร้อมแท่งสำหรับแต่ละกลุ่ม

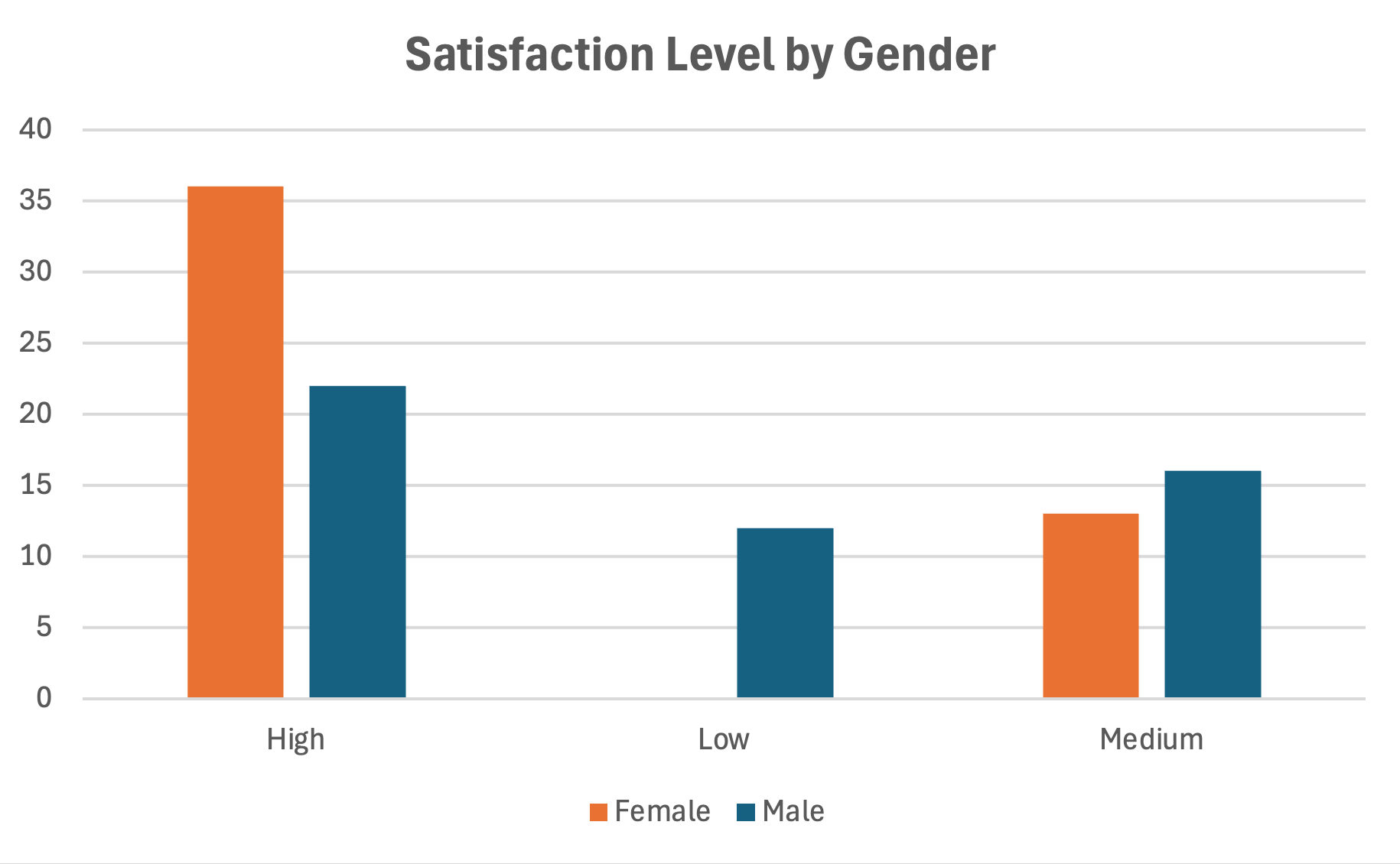Clustered bar chart comparing Male and Female responses across satisfaction levels with three clusters for Dissatisfied, Neutral, Satisfied each containing two bars colored blue for Male and orange for Female with clear legend รูปที่ 19: กราฟแท่งกลุ่มเปรียบเทียบระหว่างกลุ่ม

Histograms สำหรับตัวแปรต่อเนื่อง

สำหรับคะแนนรวมของมาตรวัดที่ใกล้เคียงข้อมูลต่อเนื่อง histograms แสดงรูปร่างการแจกแจง

  1. ใช้ Data Analysis Toolpak
  2. เลือก Histogram
  3. ระบุช่วง input และช่วง bin
  4. เลือก Chart Output

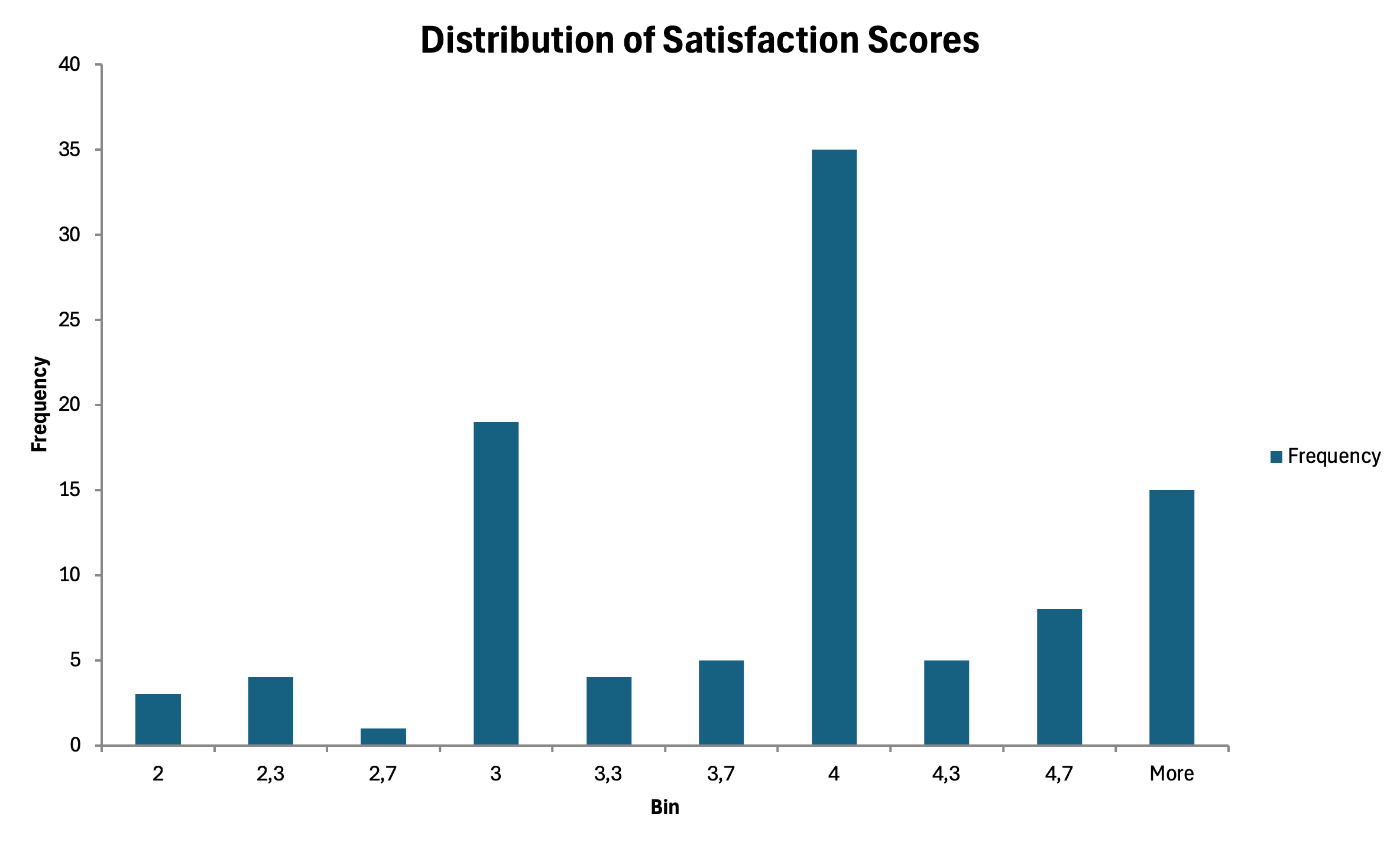Histogram showing distribution of satisfaction scale scores with x-axis showing score bins 1.0-1.9 through 5.0-5.9, y-axis showing frequency, bell-shaped distribution centered around 3.5-3.9 รูปที่ 20: ฮิสโตแกรมแสดงการกระจายของคะแนน composite scale

การจัดรูปแบบแผนภูมิสำหรับวิทยานิพนธ์

แผนภูมิทางวิชาการต้องการการจัดรูปแบบเฉพาะ:

  • ลบสิ่งรบกวนในแผนภูมิ (เส้นตาราง, ขอบ, 3D effects)
  • ใช้ grayscale หรือ patterns ถ้าพิมพ์ขาวดำ
  • ลำดับเลขรูปตามลำดับ (รูปที่ 1, รูปที่ 2)
  • วางชื่อเรื่องด้านล่างรูปในรูปแบบ APA
  • รวมหมายเหตุอธิบายคำย่อหรือขนาดกลุ่มตัวอย่าง

วิธีเขียนผลการวิจัยสำหรับวิทยานิพนธ์

การคำนวณสถิติเป็นแค่ครึ่งหนึ่งของงาน การสื่อสารผลลัพธ์อย่างชัดเจนจะกำหนดว่าอาจารย์ที่ปรึกษาจะเข้าใจผลการค้นพบของคุณหรือเปล่า ส่วนนี้จะให้ template ที่คุณสามารถปรับใช้สำหรับผลลัพธ์ของคุณเองได้เลย

พื้นฐานรูปแบบ APA

สาขาวิชาการส่วนใหญ่ใช้รูปแบบ APA สำหรับการรายงานสถิติ ข้อตกลงสำคัญ:

  • ทำตัวเอียงสัญลักษณ์สถิติ: M, SD, t, F, r, p
  • รายงานค่า p แบบตรงถึงสามตำแหน่งทศนิยม (p = .034)
  • ใช้ศูนย์นำหน้าสำหรับสถิติที่สามารถเกิน 1 (M = 0.75)
  • ไม่มีศูนย์นำหน้าสำหรับสถิติที่อยู่ในช่วง 1 (r = .67, p = .034)
  • ปัดเศษเป็นสองตำแหน่งทศนิยมเว้นแต่ต้องการความแม่นยำมากกว่า

การรายงานสถิติเชิงพรรณนา

สำหรับตัวแปรเดี่ยว:

ผู้เข้าร่วมรายงานความพึงพอใจในระดับปานกลางถึงสูงต่อบริการ (M = 3.67, SD = 0.82)

สำหรับตัวแปรแยกตามกลุ่ม:

ผู้เข้าร่วมเพศชาย (M = 3.52, SD = 0.79) รายงานความพึงพอใจต่ำกว่าผู้เข้าร่วมเพศหญิง (M = 3.78, SD = 0.84)

ในตาราง:

ตารางที่ 2 นำเสนอสถิติเชิงพรรณนาสำหรับตัวแปรในการศึกษาทั้งหมด

การรายงานผลลัพธ์ T-Test

ผลลัพธ์ที่มีนัยสำคัญ:

Independent samples t-test เผยให้เห็นความแตกต่างอย่างมีนัยสำคัญในความพึงพอใจระหว่างเพศชาย (M = 3.52, SD = 0.79) และเพศหญิง (M = 3.78, SD = 0.84), t(98) = -2.14, p = .035

ผลลัพธ์ที่ไม่มีนัยสำคัญ:

ความแตกต่างในความพึงพอใจระหว่างเพศชาย (M = 3.52, SD = 0.79) และเพศหญิง (M = 3.58, SD = 0.81) ไม่มีนัยสำคัญทางสถิติ, t(98) = -0.42, p = .677

รูปแบบคือ: t(degrees of freedom) = ค่า t, p = ค่า p

การรายงานผลลัพธ์ ANOVA

ผลลัพธ์ที่มีนัยสำคัญ:

One-way ANOVA บ่งชี้ความแตกต่างอย่างมีนัยสำคัญในความพึงพอใจระหว่างกลุ่มอายุ, F(2, 97) = 4.18, p = .018

พร้อม post-hoc:

การเปรียบเทียบ post-hoc โดยใช้ Tukey's test เผยให้เห็นว่าผู้เข้าร่วมอายุ 41 ปีขึ้นไป (M = 4.02, SD = 0.72) รายงานความพึงพอใจสูงกว่าอย่างมีนัยสำคัญเทียบกับกลุ่มอายุ 18-25 (M = 3.45, SD = 0.89), p = .014 กลุ่มอายุ 26-40 (M = 3.68, SD = 0.78) ไม่แตกต่างอย่างมีนัยสำคัญจากกลุ่มใด

การรายงานผลลัพธ์ Correlation

Correlation ที่มีนัยสำคัญ:

มีสหสัมพันธ์ทางบวกที่แข็งแกร่งระหว่างความพึงพอใจของลูกค้าและความภักดีต่อแบรนด์, r(98) = .67, p < .001 ความพึงพอใจที่สูงกว่าสัมพันธ์กับความภักดีที่มากกว่า

Correlation ที่ไม่มีนัยสำคัญ:

ความสัมพันธ์ระหว่างความพึงพอใจและอายุไม่มีนัยสำคัญทางสถิติ, r(98) = .12, p = .231

การรายงานความเชื่อมั่น

มาตรวัดเดียว:

มาตรวัดความพึงพอใจของลูกค้ามีความสอดคล้องภายในในระดับดี (Cronbach's α = .84)

หลายมาตรวัด:

ความสอดคล้องภายในอยู่ในระดับที่ยอมรับได้สำหรับทุกมาตรวัด: ความพึงพอใจของลูกค้า (α = .84), ความตั้งใจซื้อ (α = .78) และความภักดีต่อแบรนด์ (α = .91)

Template สำเร็จรูป

นี่คือ template แบบเติมคำในช่องว่างสำหรับการวิเคราะห์ทั่วไป:

Template สถิติเชิงพรรณนา:

ผู้เข้าร่วมมีคะแนน [สูง/ปานกลาง/ต่ำ] บน [ชื่อตัวแปร] (M = [ค่าเฉลี่ย], SD = [SD])

Template T-Test:

Independent samples t-test [เผยให้เห็น/ไม่เผยให้เห็น] ความแตกต่างอย่างมีนัยสำคัญใน [DV] ระหว่าง [กลุ่ม 1] (M = [ค่าเฉลี่ย], SD = [SD]) และ [กลุ่ม 2] (M = [ค่าเฉลี่ย], SD = [SD]), t([df]) = [ค่า t], p = [ค่า p]

Template ANOVA:

One-way ANOVA [บ่งชี้/ไม่บ่งชี้] ความแตกต่างอย่างมีนัยสำคัญใน [DV] ระหว่าง [ตัวแปรจัดกลุ่ม], F([df1], [df2]) = [ค่า F], p = [ค่า p]

Template Correlation:

มีสหสัมพันธ์ [แข็งแกร่ง/ปานกลาง/อ่อน] [ทางบวก/ทางลบ] ระหว่าง [ตัวแปร 1] และ [ตัวแปร 2], r([df]) = [ค่า r], p = [ค่า p]

ความผิดพลาดที่ควรหลีกเลี่ยง

แม้แต่นักวิจัยที่มีประสบการณ์ก็ทำผิดพลาดเมื่อวิเคราะห์ข้อมูลแบบสอบถาม การเรียนรู้จากความผิดพลาดที่พบบ่อยจะช่วยให้คุณได้ผลลัพธ์ที่น่าเชื่อถือมากขึ้น

ความผิดพลาดที่ 1: ใช้สถิติทดสอบผิด

การเลือกสถิติทดสอบตามสิ่งที่คุณอยากค้นพบแทนที่จะตามสิ่งที่ข้อมูลรองรับ มันจะทำให้ได้ข้อสรุปที่ผิด ให้คำถามวิจัยและประเภทข้อมูลนำทางการเลือกสถิติทดสอบเสมอนะ T-test ต้องการตัวแปรตามต่อเนื่อง Chi-square ต้องการตัวแปรเชิงกลุ่ม การผสมสิ่งเหล่านี้จะให้ผลลัพธ์ที่ไม่มีความหมาย

ความผิดพลาดที่ 2: ละเลยข้อสมมติ

สถิติ parametric สมมติการแจกแจงแบบปกติและความแปรปรวนเท่ากัน การข้ามการเช็คข้อสมมติไม่ได้ทำให้การละเมิดหายไป ลองเช็คความปกติโดยใช้ histograms หรือ Shapiro-Wilk test เช็คความเป็นเอกพันธ์ของความแปรปรวนโดยใช้ Levene's test เมื่อข้อสมมติถูกละเมิด ให้ใช้สถิติ non-parametric แทนหรือแปลงข้อมูล

ความผิดพลาดที่ 3: P-Hacking

การทำการทดสอบหลายครั้งจนกว่าจะพบนัยสำคัญ แล้วรายงานเฉพาะผลลัพธ์เหล่านั้น มันจะเพิ่มอัตราผลบวกลวง ถ้าคุณทดสอบ 20 ความสัมพันธ์ที่ α = .05 คุณคาดว่าจะได้หนึ่งผลลัพธ์ที่มีนัยสำคัญโดยบังเอิญ รายงานการวิเคราะห์ทั้งหมดที่ทำ แม้แต่ที่ไม่มีนัยสำคัญ พิจารณาการปรับสำหรับการเปรียบเทียบหลายครั้งโดยใช้ Bonferroni correction

ความผิดพลาดที่ 4: สับสนระหว่างสหสัมพันธ์กับสาเหตุ

Correlation ที่มีนัยสำคัญระหว่างความพึงพอใจและความภักดีไม่ได้พิสูจน์ว่าความพึงพอใจเป็นสาเหตุของความภักดี ความสัมพันธ์อาจกลับกัน (ความภักดีเป็นสาเหตุของความพึงพอใจ) หรือทั้งสองอาจเกิดจากตัวแปรที่สาม มีเพียงการออกแบบเชิงทดลองที่มีการสุ่มเท่านั้นที่สามารถสร้างความเป็นสาเหตุได้

ความผิดพลาดที่ 5: ตีความผลลัพธ์กลุ่มตัวอย่างเล็กมากเกินไป

สถิติทดสอบกับกลุ่มตัวอย่างเล็ก (น้อยกว่า 30 คน) มีอำนาจต่ำ หมายความว่าอาจพลาดผลที่แท้จริง พวกมันยังให้ค่าประมาณที่ไม่เสถียรซึ่งอาจไม่สามารถทำซ้ำได้ ระมัดระวังในการสรุปจากกลุ่มตัวอย่างเล็ก รายงานข้อจำกัดเรื่องขนาดกลุ่มตัวอย่างในบทอภิปรายนะ

ความผิดพลาดที่ 6: ลืมเช็คความเชื่อมั่นก่อนวิเคราะห์

การใช้มาตรวัดที่ไม่น่าเชื่อถือทำให้การวิเคราะห์ทั้งหมดในภายหลังไม่ถูกต้อง มาตรวัดที่มี α = .55 นำเสนอความคลาดเคลื่อนในการวัดมากจนความสัมพันธ์ใดๆ ที่หากพบก็น่าสงสัย ลองเช็คและรายงาน Cronbach's Alpha เสมอก่อนทำการทดสอบสมมติฐาน

ความผิดพลาดที่ 7: ไม่จัดการกับข้อมูลที่ขาดหาย

การละเลยค่าที่ขาดหายหรือจัดการอย่างไม่สอดคล้องกันสร้างอคติ บันทึกว่ามีกี่ case ที่มีข้อมูลขาดหาย ตัวแปรใดได้รับผลกระทบ และคุณจัดการปัญหาอย่างไร วิธีการทั่วไปได้แก่ listwise deletion, pairwise deletion และ mean imputation แต่ละวิธีมีข้อดีข้อเสียที่ควรยอมรับ

Excel Template: ชุดเครื่องมือวิเคราะห์แบบสอบถาม

เพื่อช่วยให้คุณนำเทคนิคเหล่านี้ไปใช้ เราสร้าง Excel template พร้อมสูตรสำเร็จรูปสำหรับการวิเคราะห์แบบสอบถามทั่วไป

สิ่งที่ template รวมอยู่:

  • Sheet สำหรับกรอกข้อมูลที่มีโครงสร้างเหมาะสม
  • การคำนวณ Cronbach's Alpha อัตโนมัติ
  • สรุปสถิติเชิงพรรณนา
  • ตัวสร้างตารางความถี่
  • เครื่องคำนวณ T-test
  • Correlation matrix
  • Template แผนภูมิ

วิธีใช้:

  1. ดาวน์โหลด template จากแถบด้านข้าง
  2. กรอกคำตอบแบบสอบถามใน sheet Data
  3. Sheet Summary จะคำนวณสถิติสำคัญโดยอัตโนมัติ
  4. ใช้ sheet Analysis สำหรับการทดสอบสมมติฐาน
  5. คัดลอก template แผนภูมิและอัปเดตด้วยข้อมูลของคุณ

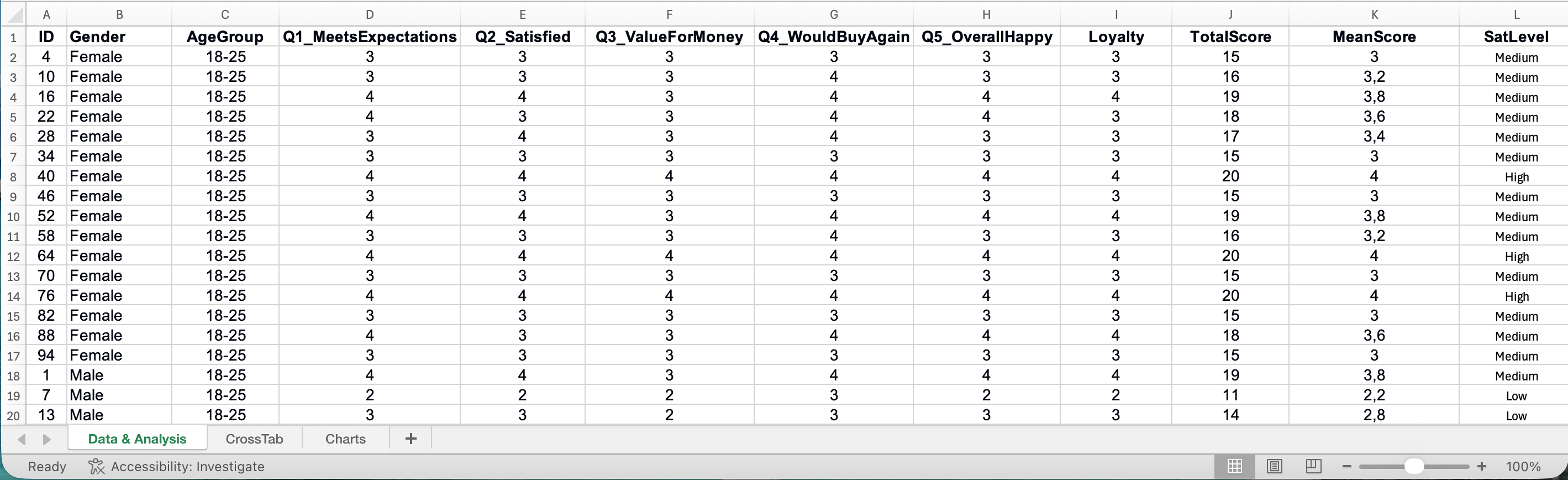Excel template showing multiple tabs including Data and Summary and Analysis and Charts with Summary sheet displaying automatic calculations for mean and SD and Cronbach's Alpha in clean labeled sections รูปที่ 21: Survey Analysis Excel Template พร้อมการคำนวณอัตโนมัติ

ดาวน์โหลด Survey Analysis Excel Template

คำถามที่พบบ่อย

ขั้นตอนต่อไป

ตอนนี้คุณมี workflow ที่สมบูรณ์สำหรับการวิเคราะห์ข้อมูลแบบสอบถามใน Excel แล้ว ตั้งแต่การเตรียมข้อมูลจนถึงการรายงานผลลัพธ์ แต่ละขั้นตอนสร้างไปสู่วิทยานิพนธ์ที่น่าเชื่อถือ

คู่มือที่เกี่ยวข้อง:

พร้อมสำหรับ SPSS หรือยัง?

ถ้าการวิเคราะห์ของคุณต้องการคุณสมบัติเกินกว่าที่ Excel มี ลองสำรวจบทเรียน SPSS ของเรา:

เอกสารอ้างอิง

Pallant, J. (2016). SPSS Survival Manual (6th ed.). McGraw-Hill Education.