คุณทำ t-test หรือ ANOVA ใน Excel สำหรับวิทยานิพนธ์เสร็จแล้ว ค่า p แสดงนัยสำคัญทางสถิติ แต่อาจารย์ที่ปรึกษาถามว่า "Effect size เท่าไหร่?"
นัยสำคัญทางสถิติบอกคุณว่ามีความแตกต่างอยู่จริง แต่ effect size บอกว่าความแตกต่างนั้นมีความหมายหรือเปล่า ค่า p = .001 กับกลุ่มตัวอย่าง 10,000 คน อาจเป็นแค่ความแตกต่างเล็กน้อยที่ไม่มีคุณค่าทางปฏิบัติ Effect size จะแสดงขนาดของผลการวิจัยโดยไม่ขึ้นกับขนาดกลุ่มตัวอย่าง
คู่มือนี้จะสอนคุณวิธีคำนวณ Cohen's d สำหรับ t-test และ eta squared สำหรับ ANOVA ใน Excel คุณจะได้เรียนรู้สูตรที่แน่นอน แนวทางการตีความตามสาขา และวิธีรายงาน effect size ในรูปแบบ APA สำหรับบทผลการวิจัยของวิทยานิพนธ์
ทำไม Effect Size ถึงสำคัญสำหรับวิทยานิพนธ์
อาจารย์ที่ปรึกษาจะประเมินทั้งนัยสำคัญทางสถิติและทางปฏิบัติ ผลที่มีนัยสำคัญทางสถิติ (p < .05) บอกแค่ว่าความแตกต่างน่าจะมีอยู่ในประชากร แต่ไม่ได้บอกว่าความแตกต่างนั้นใหญ่พอที่จะมีความหมายหรือเปล่า
Effect size ให้ข้อมูลสำคัญสามอย่างสำหรับวิทยานิพนธ์ของคุณ:
นัยสำคัญทางปฏิบัติ งานวิจัยที่มีกลุ่มตัวอย่าง 5,000 คน อาจพบว่าวิธี A ได้คะแนนสอบสูงกว่าวิธี B 2 คะแนน (p < .001) นัยสำคัญทางสถิติชัดเจน แต่คะแนนต่างกัน 2 คะแนนจากคะแนนเต็ม 100 มันมีความหมายไหม? Cohen's d จะบอกคุณได้
เปรียบเทียบข้ามงานวิจัยได้ การทบทวนวรรณกรรมของคุณเปรียบเทียบงานวิจัยที่มีขนาดกลุ่มตัวอย่างต่างกัน Effect size ทำให้ผลการวิจัยเป็นมาตรฐานเดียวกัน เพื่อให้คุณเปรียบเทียบงานที่มี n = 30 กับงานที่มี n = 3,000 ได้ ค่า p ทำแบบนี้ไม่ได้
ผลกระทบของงานวิจัย บรรณาธิการวารสารและอาจารย์ที่ปรึกษาต้องการหลักฐานว่าผลการวิจัยของคุณมีความหมายนอกเหนือจากกลุ่มตัวอย่าง Effect size เล็ก (แม้จะมีนัยสำคัญ) บ่งบอกว่าการประยุกต์ใช้ในโลกจริงอาจจำกัด Effect size ใหญ่บ่งบอกว่าการทดลองหรือผลการวิจัยของคุณมีคุณค่าทางปฏิบัติมาก
อาจารย์ที่ปรึกษาส่วนใหญ่ในปัจจุบันต้องการให้รายงาน effect size สำหรับการทดสอบทางสถิติทุกตัว APA Publication Manual ฉบับที่ 7 แนะนำอย่างชัดเจนให้รายงาน effect size ควบคู่กับค่า p ในส่วนผลการวิจัย
เมื่อไหร่ควรใช้ Cohen's d vs Eta Squared
การทดสอบทางสถิติที่คุณใช้จะเป็นตัวกำหนดว่าต้องคำนวณ effect size ตัวไหน
| การทดสอบทางสถิติ | ตัววัด Effect Size | วัดอะไร | สเกลการตีความ |
|---|---|---|---|
| Independent samples t-test | Cohen's d | ความแตกต่างมาตรฐานระหว่างค่าเฉลี่ยสองกลุ่ม | 0.2 เล็ก, 0.5 ปานกลาง, 0.8 ใหญ่ |
| Paired samples t-test | Cohen's d | ความแตกต่างมาตรฐานระหว่างการวัดแบบจับคู่ | 0.2 เล็ก, 0.5 ปานกลาง, 0.8 ใหญ่ |
| One-Way ANOVA | Eta squared (η²) หรือ Omega squared (ω²) | สัดส่วนของความแปรปรวนใน DV ที่อธิบายได้ด้วย IV | 0.01 เล็ก, 0.06 ปานกลาง, 0.14 ใหญ่ |
| Two-Way ANOVA | Partial eta squared (η²p) | ความแปรปรวนที่อธิบายได้ด้วยปัจจัยหนึ่งโดยควบคุมปัจจัยอื่น | 0.01 เล็ก, 0.06 ปานกลาง, 0.14 ใหญ่ |
ตารางที่ 1 ตัววัด effect size สำหรับการทดสอบทางสถิติที่ใช้บ่อยในวิทยานิพนธ์
ถ้าคุณเปรียบเทียบสองกลุ่ม (กลุ่มควบคุม vs กลุ่มทดลอง, ก่อน vs หลัง, ชาย vs หญิง) ให้ใช้ Cohen's d ถ้าคุณเปรียบเทียบสามกลุ่มขึ้นไป (ต่ำ/กลาง/สูง, หลายเงื่อนไขการทดลอง) ให้ใช้ eta squared หรือ omega squared จากผลลัพธ์ ANOVA
ทั้งสองตัววัดตอบคำถามเดียวกัน: Effect นี้ใหญ่แค่ไหน? แต่ใช้สเกลต่างกันเพราะวัดคนละอย่าง Cohen's d แสดง effect เป็นหน่วยของส่วนเบี่ยงเบนมาตรฐาน Eta squared แสดง effect เป็นสัดส่วนของความแปรปรวนที่อธิบายได้ (เหมือน R² ในการถดถอย)
ต้องการวิเคราะห์สถิติ?
เราสอนนักศึกษาและนักวิจัยวิเคราะห์ข้อมูลด้วย SPSS, Excel, R และ Amos
ติดต่อเราวิธีคำนวณ Cohen's d ใน Excel
Cohen's d วัดความแตกต่างมาตรฐานระหว่างค่าเฉลี่ยของสองกลุ่ม ส่วนนี้จะแสดงการคำนวณแบบ step-by-step โดยใช้สูตร Excel
ทำความเข้าใจสูตร Cohen's d
สูตรสำหรับ Cohen's d คือ:
d = (M₁ - M₂) / SDpooled
โดยที่:
- M₁ = ค่าเฉลี่ยของกลุ่ม 1
- M₂ = ค่าเฉลี่ยของกลุ่ม 2
- SDpooled = Pooled standard deviation ของทั้งสองกลุ่ม
สูตร pooled standard deviation คือ:
SDpooled = √[((n₁-1) × SD₁² + (n₂-1) × SD₂²) / (n₁ + n₂ - 2)]
โดยที่:
- n₁, n₂ = ขนาดกลุ่มตัวอย่างของกลุ่ม 1 และ 2
- SD₁, SD₂ = ส่วนเบี่ยงเบนมาตรฐานของกลุ่ม 1 และ 2
การคำนวณแบบ Step-by-Step ใน Excel
ตัวอย่างสถานการณ์: คุณทดสอบวิธีการสอนใหม่กับคะแนนสอบของนักศึกษา กลุ่มควบคุม (n = 25) มี M = 72.4, SD = 8.3 กลุ่มทดลอง (n = 28) มี M = 79.6, SD = 7.9 คำนวณ Cohen's d
หมายเหตุเกี่ยวกับตัวคั่นทศนิยม: ขึ้นอยู่กับการตั้งค่าภูมิภาค Excel อาจแสดงทศนิยมด้วยจุด (72.4) หรือจุลภาค (72,4) ทั้งสองถูกต้อง - เป็นแค่การตั้งค่า locale สูตรในคู่มือนี้ใช้จุลภาค (,) เป็นตัวคั่น argument สำหรับ Excel ภาษาไทย ถ้าสูตรไม่ทำงาน ลองเช็คตัวคั่น argument ในการตั้งค่า Excel ของคุณ
ขั้นตอนที่ 1: ตั้งค่าข้อมูลใน Excel
สร้างตารางพร้อมสถิติเชิงพรรณนา:
| สถิติ | กลุ่มควบคุม | กลุ่มทดลอง |
|---|---|---|
| ขนาดกลุ่มตัวอย่าง (n) | 25 | 28 |
| ค่าเฉลี่ย (M) | 72.4 | 79.6 |
| ส่วนเบี่ยงเบนมาตรฐาน (SD) | 8.3 | 7.9 |
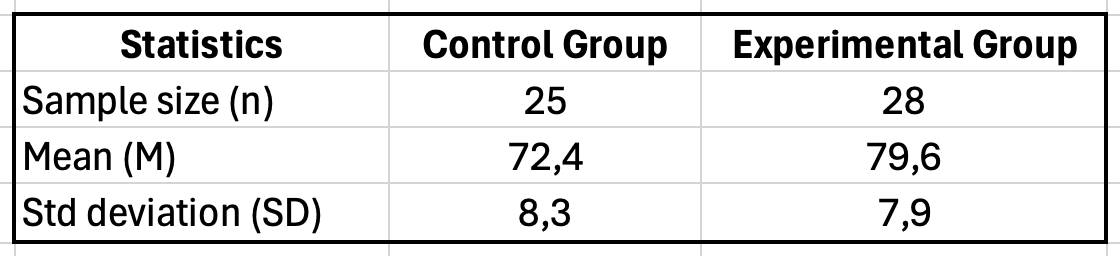
รูปที่ 1: การตั้งค่าตาราง Excel สำหรับคำนวณ Cohen's d แสดงขนาดกลุ่มตัวอย่าง ค่าเฉลี่ย และส่วนเบี่ยงเบนมาตรฐานสำหรับกลุ่มควบคุมและกลุ่มทดลอง
ขั้นตอนที่ 2: คำนวณ pooled standard deviation
ในเซลล์ใหม่ (เช่น B7) ใส่สูตรนี้:
=SQRT(((B2-1)*B4^2 + (C2-1)*C4^2)/(B2+C2-2))
สูตรนี้คำนวณ: √[((25-1) × 8.3² + (28-1) × 7.9²) / (25 + 28 - 2)]
ผลลัพธ์: SDpooled = 8.09
ขั้นตอนที่ 3: คำนวณ Cohen's d
ในเซลล์ B8 ใส่:
=ABS(B3-C3)/B7
สูตรนี้คำนวณ: |72.4 - 79.6| / 8.09
ผลลัพธ์: d = 0.89
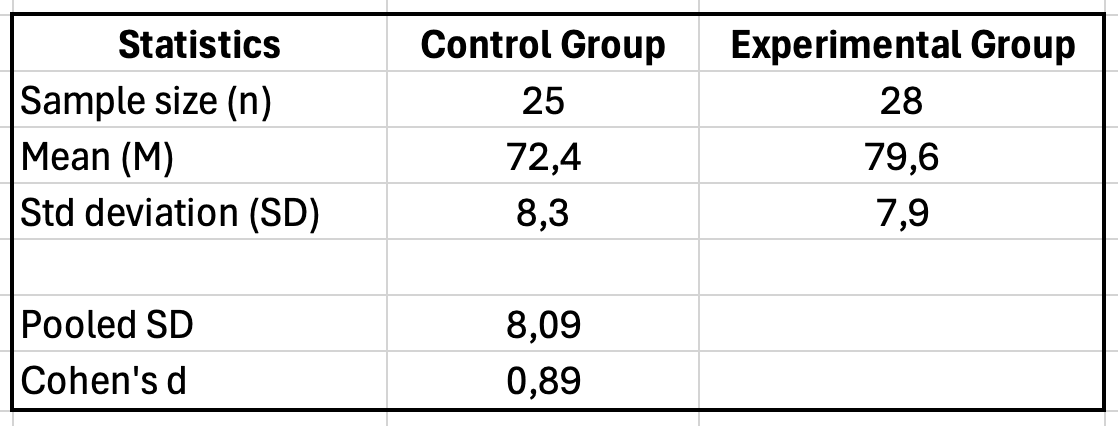
รูปที่ 2: การคำนวณ Cohen's d ใน Excel แสดง pooled standard deviation 8.09 และผลลัพธ์ Cohen's d 0.89
ทางเลือก: ใช้สถิติเชิงพรรณนาโดยตรง
ถ้าคุณทำ t-test เสร็จแล้วและมีสถิติเชิงพรรณนา คุณสามารถสร้างเครื่องคำนวณ Cohen's d อย่างง่ายใน Excel:
| เซลล์ | ป้ายกำกับ | สูตร/ค่า | คำอธิบาย |
|---|---|---|---|
| A1 | ค่าเฉลี่ยกลุ่ม 1 | 72.4 | ใส่ค่า M₁ |
| A2 | ค่าเฉลี่ยกลุ่ม 2 | 79.6 | ใส่ค่า M₂ |
| A3 | SD กลุ่ม 1 | 8.3 | ใส่ค่า SD₁ |
| A4 | SD กลุ่ม 2 | 7.9 | ใส่ค่า SD₂ |
| A5 | n กลุ่ม 1 | 25 | ใส่ค่า n₁ |
| A6 | n กลุ่ม 2 | 28 | ใส่ค่า n₂ |
| A7 | Pooled SD | =SQRT(((A5-1)*A3^2+(A6-1)*A4^2)/(A5+A6-2)) | คำนวณอัตโนมัติ |
| A8 | Cohen's d | =ABS(A1-A2)/A7 | Effect size ของคุณ |
ตารางที่ 2 แม่แบบเครื่องคำนวณ Cohen's d สำหรับ Excel (บันทึกเป็นแม่แบบที่ใช้ซ้ำได้)
บันทึกแม่แบบนี้ไว้สำหรับคำนวณ Cohen's d อย่างรวดเร็วตลอดการวิเคราะห์วิทยานิพนธ์ของคุณ
วิธีคำนวณ Cohen's d สำหรับ Paired Samples ใน Excel
สูตรด้านบนใช้สำหรับ independent samples (สองกลุ่มต่างกัน) ถ้าคุณเปรียบเทียบผู้เข้าร่วมคนเดียวกันในสองช่วงเวลา (pre-test vs post-test, ก่อน vs หลังการทดลอง) คุณต้องใช้การคำนวณที่ต่างออกไป
ทำความเข้าใจสูตรสำหรับ Paired Samples
สำหรับ paired samples, Cohen's d ใช้ค่าเฉลี่ยของผลต่างและส่วนเบี่ยงเบนมาตรฐานของผลต่าง:
d = Mean of differences / SD of differences
บางครั้งเรียกว่า dz (d-sub-z) ในเอกสารวิชาการ มันคำนึงถึงว่าการสังเกตแบบจับคู่มีความสัมพันธ์กัน
การคำนวณแบบ Step-by-Step ใน Excel
ตัวอย่างสถานการณ์: คุณวัดคะแนนความวิตกกังวลของผู้เข้าร่วม 30 คน ก่อนและหลังการทดลอง mindfulness คุณต้องคำนวณ effect size สำหรับการเปรียบเทียบ pre-post
ขั้นตอนที่ 1: คำนวณผลต่างสำหรับผู้เข้าร่วมแต่ละคน
ถ้าคะแนน pre-test อยู่ในคอลัมน์ A (A2:A31) และคะแนน post-test อยู่ในคอลัมน์ B (B2:B31) สร้างคอลัมน์ผลต่างในคอลัมน์ C:
=B2-A2
คัดลอกสูตรนี้ลงไปสำหรับผู้เข้าร่วมทั้ง 30 คน
ขั้นตอนที่ 2: คำนวณค่าเฉลี่ยของผลต่าง
ในเซลล์ด้านล่างข้อมูล (เช่น C33):
=AVERAGE(C2:C31)
ผลลัพธ์ตัวอย่าง: Mean difference = -8.4 (ค่าลบหมายความว่าความวิตกกังวลลดลง)
ขั้นตอนที่ 3: คำนวณส่วนเบี่ยงเบนมาตรฐานของผลต่าง
ในเซลล์ C34:
=STDEV.S(C2:C31)
ผลลัพธ์ตัวอย่าง: SD of differences = 6.2
ขั้นตอนที่ 4: คำนวณ Cohen's d
ในเซลล์ C35:
=ABS(C33)/C34
สูตรนี้คำนวณ: |−8.4| / 6.2 = 1.35
ผลลัพธ์: d = 1.35 (effect ใหญ่มาก)
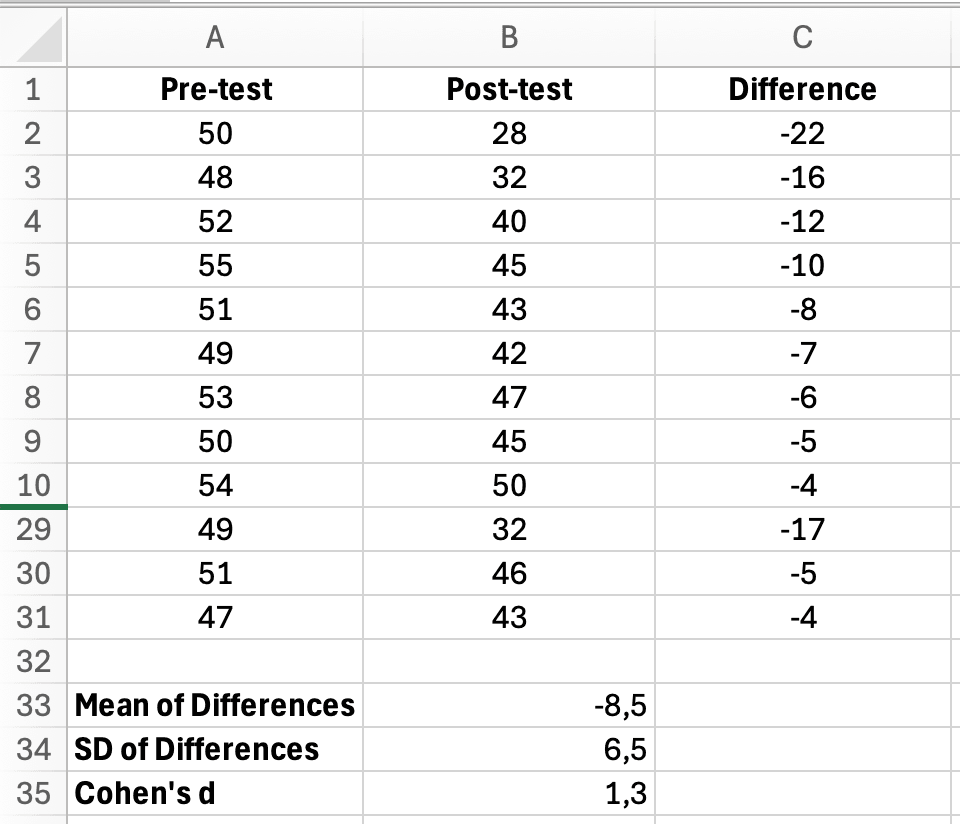
รูปที่ 3: การคำนวณ Cohen's d สำหรับ paired samples ใน Excel แสดงคอลัมน์ Pre-test, Post-test, Difference พร้อมค่าเฉลี่ยของผลต่าง, SD และผลลัพธ์ Cohen's d 1.3
แม่แบบเครื่องคำนวณสำหรับ Paired Samples
สร้างแม่แบบที่ใช้ซ้ำได้นี้สำหรับ effect size ของ paired samples:
| เซลล์ | ป้ายกำกับ | สูตร/ค่า | คำอธิบาย |
|---|---|---|---|
| A1 | Mean of Differences | =AVERAGE(difference_range) | การเปลี่ยนแปลงเฉลี่ย pre-post |
| A2 | SD of Differences | =STDEV.S(difference_range) | ความแปรปรวนในคะแนนการเปลี่ยนแปลง |
| A3 | Cohen's d (paired) | =ABS(A1)/A2 | Effect size ของคุณ |
ตารางที่ 3 แม่แบบเครื่องคำนวณ Cohen's d สำหรับ paired samples ใน Excel (การออกแบบ pre-post)
หมายเหตุสำคัญ: Effect Size ของ Paired vs Independent
Effect size จากการออกแบบ paired (dz) มักจะใหญ่กว่าการออกแบบ independent เพราะ SD ของผลต่างมักจะเล็กกว่า pooled SD ของคะแนนดิบ นี่ไม่ใช่ข้อผิดพลาด - มันสะท้อนความแม่นยำที่เพิ่มขึ้นของการเปรียบเทียบ within-subjects
เมื่อเปรียบเทียบ effect size ของคุณกับงานวิจัยที่ตีพิมพ์ ให้ตรวจสอบว่างานวิจัยเหล่านั้นใช้การออกแบบ paired หรือ independent ถ้าต้องการเปรียบเทียบข้ามประเภทการศึกษา นักวิจัยบางคนคำนวณ Cohen's d โดยใช้ค่าเฉลี่ยของส่วนเบี่ยงเบนมาตรฐาน pre และ post (เรียกว่า dav) แทน SD ของผลต่าง
วิธีคำนวณ Eta Squared ใน Excel
Eta squared (η²) วัดสัดส่วนของความแปรปรวนทั้งหมดในตัวแปรตามที่อธิบายได้ด้วยตัวแปรอิสระใน ANOVA ส่วนนี้จะแสดงวิธีดึงและคำนวณจากผลลัพธ์ ANOVA ของ Excel
ทำความเข้าใจสูตร Eta Squared
สูตรสำหรับ eta squared คือ:
η² = SSBetween / SSTotal
โดยที่:
- SSBetween = Sum of Squares Between Groups (ความแปรปรวนที่อธิบายได้ด้วยตัวแปรจัดกลุ่ม)
- SSTotal = Total Sum of Squares (ความแปรปรวนทั้งหมดในข้อมูล)
Eta squared บอกคุณว่ากี่เปอร์เซ็นต์ของความแปรปรวนในตัวแปรตามที่เกิดจากตัวแปรอิสระ η² = 0.25 หมายความว่าตัวแปรจัดกลุ่มอธิบาย 25% ของความแปรปรวนในผลลัพธ์
การคำนวณแบบ Step-by-Step จากผลลัพธ์ ANOVA
ตัวอย่างสถานการณ์: คุณเปรียบเทียบคะแนนความผูกพันของนักศึกษาระหว่างสามวิธีการสอน (traditional, blended, online) คุณทำ One-Way ANOVA ใน Excel และต้องคำนวณ effect size
ขั้นตอนที่ 1: ทำ One-Way ANOVA ใน Excel
ขั้นแรก ทำ ANOVA โดยใช้ Data Analysis ToolPak (ถ้ายังไม่ได้เปิดใช้งาน ดูคู่มือวิธีเปิดใช้งาน Data Analysis ใน Excel) สำหรับคำแนะนำรายละเอียดการทำ ANOVA ดูคู่มือฉบับสมบูรณ์วิธีคำนวณ ANOVA ใน Excel
- คลิก Data > Data Analysis > Anova: Single Factor
- เลือกช่วงข้อมูล (สามกลุ่มของคะแนนความผูกพัน)
- ติ๊ก "Labels in First Row" ถ้ามี
- คลิก OK
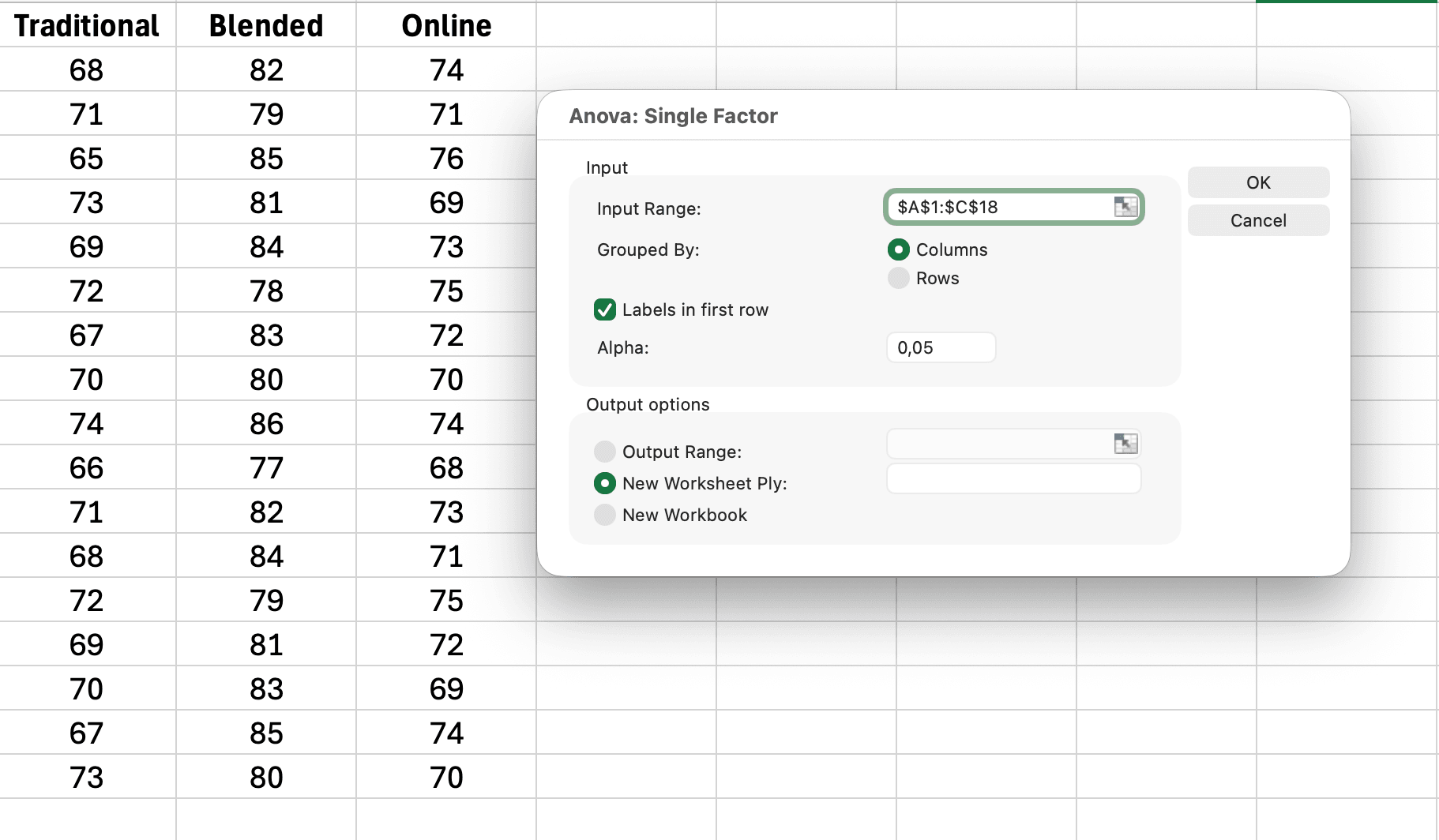
รูปที่ 4: กล่องโต้ตอบ Excel Data Analysis ANOVA Single Factor แสดงช่วงอินพุต ติ๊กป้ายกำกับในแถวแรก และตัวเลือกเอาต์พุต
ขั้นตอนที่ 2: หาค่า Sum of Squares
ตารางผลลัพธ์ ANOVA ของ Excel จะมีลักษณะแบบนี้:
| Source of Variation | SS | df | MS | F | P-value |
|---|---|---|---|---|---|
| Between Groups | 245.6 | 2 | 122.8 | 8.34 | 0.001 |
| Within Groups | 278.2 | 47 | 5.92 | ||
| Total | 523.8 | 49 |
ตารางที่ 4 ตัวอย่างผลลัพธ์ One-Way ANOVA จาก Excel (คะแนนความผูกพันตามวิธีการสอน)
คุณต้องการสองค่า:
- SS Between Groups = 245.6 (ความแปรปรวนที่อธิบายได้ด้วยวิธีการสอน)
- SS Total = 523.8 (ความแปรปรวนทั้งหมดในคะแนนความผูกพัน)
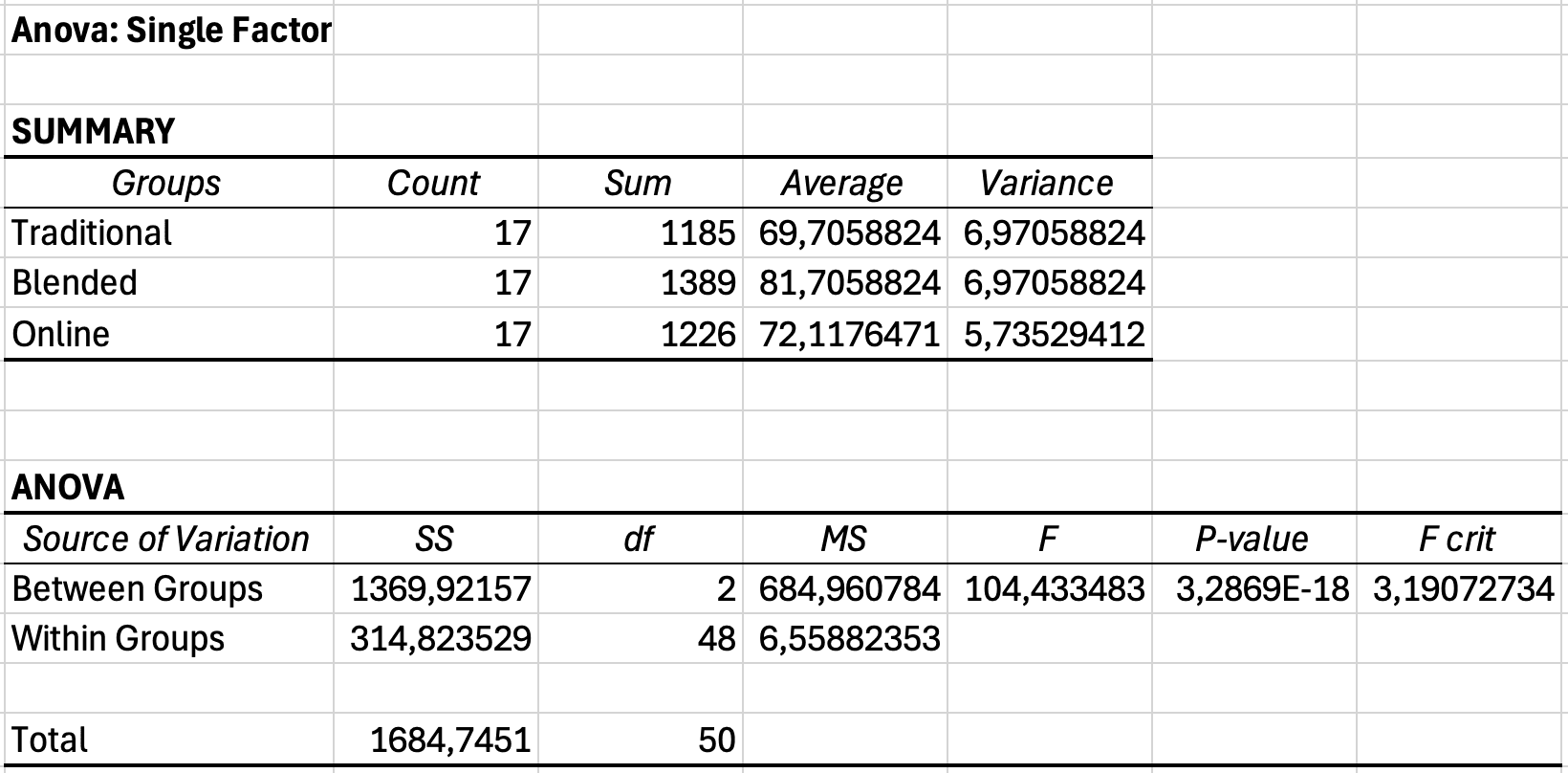
รูปที่ 5: ตารางผลลัพธ์ ANOVA ของ Excel แสดงค่า Sum of Squares Between Groups และ Total ที่ต้องใช้สำหรับคำนวณ eta squared
ขั้นตอนที่ 3: คำนวณ eta squared
ในเซลล์ด้านล่างตาราง ANOVA ใส่:
=B10/B12
(ปรับการอ้างอิงเซลล์ให้ตรงกับตำแหน่งที่ SS Between และ SS Total ปรากฏ)
สูตรนี้คำนวณ: 245.6 / 523.8 = 0.469
ขั้นตอนที่ 4: แปลงเป็นเปอร์เซ็นต์ (ตัวเลือก)
เพื่อแสดงเป็นเปอร์เซ็นต์ของความแปรปรวนที่อธิบายได้:
=B10/B12*100
ผลลัพธ์: η² = 0.469 หรือ 46.9% ของความแปรปรวนที่อธิบายได้
สร้างเครื่องคำนวณ Eta Squared ใน Excel
สำหรับการคำนวณอย่างรวดเร็ว สร้างแม่แบบง่ายๆ ข้างๆ ผลลัพธ์ ANOVA:
| เซลล์ | ป้ายกำกับ | สูตร/ค่า |
|---|---|---|
| D1 | SS Between | =B10 |
| D2 | SS Total | =B12 |
| D3 | Eta Squared (η²) | =D1/D2 |
| D4 | % Variance Explained | =D3*100 |
ตารางที่ 5 แม่แบบเครื่องคำนวณ eta squared สำหรับผลลัพธ์ ANOVA ใน Excel
แม่แบบนี้จะอัพเดทอัตโนมัติเมื่อคุณทำการวิเคราะห์ ANOVA ใหม่
การตีความ Effect Size สำหรับวิทยานิพนธ์
การคำนวณ effect size เป็นแค่ขั้นตอนแรก อาจารย์ที่ปรึกษาคาดหวังให้คุณตีความว่า effect ของคุณเล็ก ปานกลาง หรือใหญ่ และมันหมายความว่าอย่างไรสำหรับคำถามวิจัย
แนวทางการตีความ Cohen's d
Jacob Cohen (1988) เสนอเกณฑ์เหล่านี้สำหรับการวิจัยพฤติกรรมศาสตร์:
| ค่า Cohen's d | ขนาด Effect | ตำแหน่ง Percentile | การทับซ้อนระหว่าง Distribution |
|---|---|---|---|
| 0.2 | เล็ก | Percentile ที่ 58 | 85% ทับซ้อน |
| 0.5 | ปานกลาง | Percentile ที่ 69 | 67% ทับซ้อน |
| 0.8 | ใหญ่ | Percentile ที่ 79 | 53% ทับซ้อน |
| 1.0 | ใหญ่มาก | Percentile ที่ 84 | 45% ทับซ้อน |
ตารางที่ 6 การตีความ Cohen's d พร้อมความหมายทางปฏิบัติ (percentile = คนเฉลี่ยในกลุ่มทดลองอยู่ที่ตำแหน่งไหนในกลุ่มควบคุม)
ตัวอย่างการตีความทางปฏิบัติ: ถ้าการทดลองของคุณให้ d = 0.8 คนเฉลี่ยในกลุ่มทดลองจะอยู่ที่ percentile ที่ 79 ของกลุ่มควบคุม หมายความว่า 79% ของกลุ่มควบคุมได้คะแนนต่ำกว่าผู้เข้าร่วมเฉลี่ยในกลุ่มทดลอง
แนวทางการตีความ Eta Squared
สำหรับ effect size ของ ANOVA, Cohen แนะนำว่า:
- η² = 0.01 (1% ความแปรปรวนที่อธิบายได้) = Effect เล็ก
- η² = 0.06 (6% ความแปรปรวนที่อธิบายได้) = Effect ปานกลาง
- η² = 0.14 (14% ความแปรปรวนที่อธิบายได้) = Effect ใหญ่
ตัวอย่างการตีความ: ANOVA วิธีการสอนของคุณให้ η² = 0.47 (47% ความแปรปรวนที่อธิบายได้) นี่คือ effect ที่ใหญ่มาก วิธีการสอนอธิบายเกือบครึ่งหนึ่งของความแปรปรวนในความผูกพันของนักศึกษา อีก 53% ที่เหลือเกิดจากความแตกต่างระหว่างบุคคล, ความคลาดเคลื่อนในการวัด และปัจจัยอื่นที่ไม่ได้วัด
ข้อพิจารณาเฉพาะสาขา
เกณฑ์ของ Cohen ไม่ใช่มาตรฐานสากล มาตรฐาน effect size แตกต่างกันตามสาขา:
การวิจัยด้านการศึกษา: d เฉลี่ย = 0.4 สำหรับการทดลองการสอน Effect d = 0.2 เป็นเรื่องปกติและยังมีนัยสำคัญทางปฏิบัติสำหรับการนำไปใช้ในห้องเรียน
จิตวิทยาคลินิก: Effect ของการรักษา d ในช่วง 0.5-0.8 เป็นเรื่องปกติ Effect เล็กกว่า (d ในช่วง 0.2-0.4) ก็อาจมีความหมายทางคลินิกสำหรับโรคเรื้อรัง
การแพทย์และสาธารณสุข: แม้ d = 0.1 ก็อาจเป็นความแตกต่างที่สำคัญเมื่อการทดลองส่งผลต่ออัตราการเสียชีวิตหรือการเกิดโรค นัยสำคัญทางสถิติสำคัญกว่าขนาดของ effect size
จิตวิทยาทดลอง: การศึกษาในห้องปฏิบัติการมักแสดง effect ใหญ่ (d > 1.0) ภายใต้เงื่อนไขที่ควบคุม การศึกษาภาคสนามมักแสดง effect เล็กกว่า (d ในช่วง 0.3-0.5)
ธุรกิจและการจัดการ: Effect d ในช่วง 0.3-0.5 เป็นเรื่องปกติสำหรับการทดลองในองค์กร การวิเคราะห์ต้นทุน-ผลประโยชน์สำคัญกว่าขนาดของ effect size
วิทยานิพนธ์ของคุณควรอ้างอิง meta-analyses ที่ตีพิมพ์ในสาขาวิจัยเฉพาะของคุณเพื่อให้บริบทแก่ effect size ระบุในส่วนอภิปราย: "Effect ที่สังเกตได้ (d = 0.52) สอดคล้องกับ effect เฉลี่ยที่รายงานใน meta-analysis ของ Smith และคณะ (2023) สำหรับการทดลองที่คล้ายกัน (d = 0.48, 95% CI 0.41 ถึง 0.55)"
ต้องการวิเคราะห์สถิติ?
เราสอนนักศึกษาและนักวิจัยวิเคราะห์ข้อมูลด้วย SPSS, Excel, R และ Amos
ติดต่อเราวิธีรายงาน Effect Size ในรูปแบบ APA
APA Publication Manual (ฉบับที่ 7) กำหนดให้รายงาน effect size สำหรับการทดสอบ inferential ทั้งหมดในส่วนผลการวิจัยของวิทยานิพนธ์ Effect size รายงานควบคู่กับสถิติเชิงพรรณนาเช่นค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐาน ซึ่งให้บริบทที่ผู้อ่านต้องการในการตีความผลการวิจัย ส่วนนี้จะแสดงรูปแบบที่แน่นอน
การรายงาน Cohen's d สำหรับ T-Test
รูปแบบ: ใส่ Cohen's d ในวงเล็บทันทีหลังค่า p
ตัวอย่างที่ 1: Independent samples t-test
Independent samples t-test พบว่านักศึกษาในกลุ่มทดลอง (M = 79.6, SD = 7.9) ได้คะแนนสูงกว่ากลุ่มควบคุม (M = 72.4, SD = 8.3) อย่างมีนัยสำคัญ, t(51) = 3.21, p = .002, d = 0.89 Effect size มีขนาดใหญ่ บ่งชี้ว่าการทดลองมีผลกระทบมากต่อผลการสอบ
ตัวอย่างที่ 2: Paired samples t-test
Paired samples t-test พบว่าคะแนนคำศัพท์เพิ่มขึ้นอย่างมีนัยสำคัญจาก pretest (M = 64.2, SD = 9.1) ถึง posttest (M = 71.8, SD = 8.6), t(34) = 4.12, p < .001, d = 0.70 นี่คือ effect ขนาดปานกลางถึงใหญ่
ตัวอย่างที่ 3: ผลลัพธ์ไม่มีนัยสำคัญพร้อม effect size
ไม่พบความแตกต่างที่มีนัยสำคัญในอัตราการคงอยู่ระหว่างการสอนออนไลน์ (M = 85.2, SD = 12.3) และการสอนในห้อง (M = 87.1, SD = 11.8), t(78) = 0.71, p = .481, d = 0.16 Effect size เล็กบ่งบอกว่ารูปแบบการส่งมอบมีผลกระทบน้อยต่อการคงอยู่
หมายเหตุ: รายงาน effect size แม้ผลลัพธ์ไม่มีนัยสำคัญ Effect เล็กที่ไม่มีนัยสำคัญบอกเรื่องราวที่ต่างจาก effect ปานกลางที่ไม่ถึงนัยสำคัญเพราะ power ต่ำ
การรายงาน Eta Squared สำหรับ ANOVA
รูปแบบ: ใส่ η² หลังสถิติ F และค่า p
ตัวอย่างที่ 1: One-Way ANOVA
One-way ANOVA พบ effect ที่มีนัยสำคัญของวิธีการสอนต่อความผูกพันของนักศึกษา, F(2, 47) = 8.34, p = .001, η² = .26 วิธีการสอนอธิบาย 26% ของความแปรปรวนในคะแนนความผูกพัน ซึ่งเป็น effect ใหญ่ตามเกณฑ์ของ Cohen (1988)
ตัวอย่างที่ 2: การตีความต่อเนื่อง
วิธีการสอนมี effect ที่มีนัยสำคัญต่อคะแนนสอบปลายภาค, F(2, 87) = 12.45, p < .001, η² = .22 การทดสอบ post-hoc Tukey พบว่าการเรียนแบบ blended (M = 84.3, SD = 7.2) ดีกว่าทั้งการสอนแบบ traditional (M = 76.8, SD = 9.1, p = .001) และออนไลน์เต็มรูปแบบ (M = 78.2, SD = 8.6, p = .008) Effect size ใหญ่บ่งบอกว่ารูปแบบการสอนเป็นตัวกำหนดสำคัญของผลการเรียนในบริบทนี้
ตัวอย่างที่ 3: การเปรียบเทียบหลายรายการ
ANOVA พบความแตกต่างที่มีนัยสำคัญในความพึงพอใจในงานระหว่างแผนก, F(3, 131) = 5.67, p = .001, η² = .12 แม้ effect size จะปานกลาง การเปรียบเทียบ post-hoc พบว่าความแตกต่างเกิดจากความพึงพอใจที่ต่ำกว่าในฝ่าย Operations (M = 3.2, SD = 1.1) เมื่อเทียบกับ Sales (M = 4.1, SD = 0.9, p < .001) และ Marketing (M = 4.0, SD = 0.8, p = .002)
การรายงานในตาราง
สำหรับการเปรียบเทียบหลายรายการ สร้างตารางสรุป:
| การเปรียบเทียบ | M1 | M2 | t | df | p | d |
|---|---|---|---|---|---|---|
| ควบคุม vs ทดลอง | 72.4 | 79.6 | 3.21 | 51 | .002 | 0.89 |
| Pretest vs Posttest | 64.2 | 71.8 | 4.12 | 34 | <.001 | 0.70 |
| ออนไลน์ vs ในห้อง | 85.2 | 87.1 | 0.71 | 78 | .481 | 0.16 |
ตารางที่ 7 สรุปผลลัพธ์ t-test พร้อม effect size สำหรับการเปรียบเทียบการสอนสามรายการ
ตีความ effect size ในเนื้อหาเสมอ ไม่ใช่แค่ในตาราง เชื่อมโยงผลทางสถิติกับคำถามวิจัยและนัยสำคัญทางปฏิบัติ
แนวปฏิบัติที่ดีที่สุด: Confidence Intervals สำหรับ Effect Size
APA ฉบับที่ 7 แนะนำให้รายงาน 95% confidence intervals (CIs) สำหรับ effect size ไม่ใช่แค่ค่าประมาณจุดเดียว ตัวอย่าง: "d = 0.89, 95% CI [0.51, 1.27]" Confidence intervals แสดงความแม่นยำของการประมาณ effect size และช่วยผู้อ่านประเมินว่า effect อาจทับซ้อนกันระหว่างเงื่อนไขหรือไม่
การคำนวณ CIs สำหรับ effect size ใน Excel ค่อนข้างซับซ้อนและมักต้องใช้สูตรเฉพาะหรือซอฟต์แวร์ สำหรับวิทยานิพนธ์ คุณสามารถใช้เครื่องคำนวณออนไลน์ฟรี (ค้นหา "Cohen's d confidence interval calculator") หรือซอฟต์แวร์สถิติเช่น JASP หรือ jamovi ถ้าอาจารย์ต้องการ CIs ให้ระบุข้อจำกัดนี้และให้ค่าประมาณจุดพร้อมหมายเหตุว่าการคำนวณ CI ต้องใช้เครื่องมือภายนอก
ข้อผิดพลาดที่พบบ่อยเมื่อคำนวณ Effect Size
ข้อผิดพลาดเหล่านี้ปรากฏบ่อยในร่างวิทยานิพนธ์ หลีกเลี่ยงเพื่อป้องกันการแก้ไขจากอาจารย์
ข้อผิดพลาดที่ 1: ใช้ Standard Deviation ผิดสำหรับ Cohen's d
วิธีที่ผิด: ใช้ส่วนเบี่ยงเบนมาตรฐานของกลุ่มเดียว หรือค่าเฉลี่ยของ SD ทั้งสอง
ทำไมถึงผิด: Cohen's d ต้องใช้ pooled standard deviation ซึ่งถ่วงน้ำหนักความแปรปรวนของแต่ละกลุ่มตามขนาดกลุ่มตัวอย่าง การใช้ SD₁ หรือ (SD₁ + SD₂)/2 ทำให้ได้ค่าประมาณ effect size ที่ไม่ถูกต้อง
วิธีที่ถูกต้อง: ใช้สูตร pooled SD เสมอ:
SD_pooled = SQRT(((n1-1)*SD1^2 + (n2-1)*SD2^2)/(n1+n2-2))
ตัวอย่าง: กลุ่ม 1 (n=15, SD=5.2), กลุ่ม 2 (n=35, SD=7.8)
- ผิด: SD เฉลี่ย (5.2 + 7.8) / 2 = 6.5
- ถูก: Pooled SD = 7.1 (กลุ่มตัวอย่างที่ใหญ่กว่าของกลุ่ม 2 มีน้ำหนักมากกว่า)
ทางเลือกสำหรับความแปรปรวนไม่เท่ากัน: ถ้าความแปรปรวนของกลุ่มต่างกันมาก (SD หนึ่งมากกว่าสองเท่าของอีกตัว) พิจารณาใช้ Glass's delta (Δ) แทน Glass's Δ ใช้แค่ส่วนเบี่ยงเบนมาตรฐานของกลุ่มควบคุมเป็นตัวหาร: Δ = (M₁ - M₂) / SD_control วิธีนี้เหมาะสมเมื่อการทดลองอาจส่งผลต่อความแปรปรวนรวมถึงค่าเฉลี่ย
ข้อผิดพลาดที่ 2: ตีความ Eta Squared เหมือน Cohen's d
การตีความที่ผิด: "η² ของผม = 0.25 ซึ่งเป็น effect เล็กเพราะน้อยกว่า 0.5"
ทำไมถึงผิด: Eta squared และ Cohen's d ใช้สเกลต่างกัน η² = 0.25 หมายถึง 25% ของความแปรปรวนที่อธิบายได้ ซึ่งเป็น effect ใหญ่มาก Cohen's d = 0.25 จะเป็น effect เล็กถึงปานกลาง
การตีความที่ถูกต้อง: ใช้เกณฑ์ที่เหมาะสม สำหรับ η²: 0.01 เล็ก, 0.06 ปานกลาง, 0.14 ใหญ่ สำหรับ d: 0.2 เล็ก, 0.5 ปานกลาง, 0.8 ใหญ่
ข้อผิดพลาดที่ 3: รายงาน Effect Size เฉพาะผลที่มีนัยสำคัญ
แนวปฏิบัติที่ผิด: คำนวณและรายงาน Cohen's d เฉพาะเมื่อ p < .05
ทำไมถึงผิด: Effect size เป็นอิสระจากนัยสำคัญทางสถิติ ผลที่ไม่มีนัยสำคัญแต่มี effect size ปานกลาง (d = 0.5, p = .08) บอกคุณว่า effect มีอยู่แต่กลุ่มตัวอย่างเล็กเกินไปที่จะตรวจพบ นี่เป็นข้อมูลที่มีคุณค่าสำหรับข้อเสนอแนะการวิจัยในอนาคต
แนวปฏิบัติที่ถูกต้อง: รายงาน effect size สำหรับการเปรียบเทียบทั้งหมด โดยไม่คำนึงถึงค่า p ในส่วนอภิปราย อธิบาย: "แม้ความแตกต่างไม่ถึงนัยสำคัญทางสถิติ (p = .08) effect size ปานกลาง (d = 0.52) บ่งบอกว่าการทดลองอาจมีคุณค่าทางปฏิบัติ กลุ่มตัวอย่างที่ใหญ่กว่าจะมี power เพียงพอในการตรวจจับ effect นี้"
ข้อผิดพลาดที่ 4: สับสน Eta Squared กับ Partial Eta Squared
ความแตกต่าง:
- Eta squared (η²) = SSeffect / SStotal (ความแปรปรวนที่อธิบายได้จากความแปรปรวนทั้งหมด)
- Partial eta squared (η²p) = SSeffect / (SSeffect + SSerror) (ความแปรปรวนที่อธิบายได้จากความแปรปรวนที่เหลือ)
เมื่อไหร่มันสำคัญ: สำหรับ one-way ANOVA ทั้งสองเหมือนกัน สำหรับ factorial ANOVA (ตัวแปรอิสระสองตัวขึ้นไป) มันต่างกัน SPSS รายงาน partial eta squared เป็นค่าเริ่มต้น
วิธีที่ถูกต้อง: สำหรับ one-way ANOVA ใน Excel รายงาน eta squared ถ้าใช้ SPSS หรือซอฟต์แวร์อื่นที่มีหลายปัจจัย รายงาน partial eta squared และระบุในเนื้อหา: "F(2, 87) = 8.34, p = .001, η²p = .16"
ข้อผิดพลาดที่ 5: ไม่สนใจ Effect Size ที่เป็นลบ
วิธีที่ผิด: รายงาน d = 0.45 เมื่อกลุ่ม 1 ได้คะแนนต่ำกว่ากลุ่ม 2 โดยไม่ระบุทิศทาง
ทำไมถึงมีปัญหา: Effect size สามารถเป็นบวกหรือลบขึ้นอยู่กับว่ากลุ่มไหนสูงกว่า นี่สำคัญสำหรับการตีความ โดยเฉพาะเมื่อเปรียบเทียบงานวิจัยหลายชิ้น
วิธีที่ถูกต้อง: รายงานเครื่องหมายเมื่อทิศทางสำคัญ หรือใช้ค่าสัมบูรณ์และระบุทิศทางในเนื้อหา ตัวอย่าง: "กลุ่มควบคุมทำได้ดีกว่ากลุ่มทดลองอย่างมีนัยสำคัญ, t(48) = 2.34, p = .023, d = -0.45" หรือ "...d = 0.45 ในทิศทางที่เอื้อประโยชน์ต่อกลุ่มควบคุม"
หัวข้อขั้นสูง: Omega Squared vs Eta Squared
Eta squared มีข้อจำกัดที่รู้จักกัน: มันประมาณค่า effect size สูงเกินไป โดยเฉพาะกับกลุ่มตัวอย่างเล็ก Omega squared (ω²) ให้ค่าประมาณที่ไม่เอนเอียงของ effect size ประชากร
เมื่อไหร่ควรใช้ Omega Squared
พิจารณารายงาน omega squared แทน eta squared เมื่อ:
- ขนาดกลุ่มตัวอย่างเล็ก (n < 30 ต่อกลุ่ม)
- คุณต้องการสรุปผลไปยังประชากร (วิทยานิพนธ์)
- สาขาของคุณนิยมค่าประมาณที่ไม่เอนเอียง (เช็คงานวิจัยที่ตีพิมพ์ในสาขาของคุณ)
การคำนวณ Omega Squared ใน Excel
สูตรสำหรับ omega squared คือ:
ω² = (SSBetween - (dfBetween × MSWithin)) / (SSTotal + MSWithin)
ใช้ตัวอย่าง ANOVA ก่อนหน้า:
- SSBetween = 245.6
- dfBetween = 2
- MSWithin = 5.92 (จากแถว Within Groups)
- SSTotal = 523.8
=(245.6 - (2*5.92))/(523.8 + 5.92)
ผลลัพธ์: ω² = 0.447 (เทียบกับ η² = 0.469)
Omega squared มักจะน้อยกว่า eta squared 1-3% ทั้งสองนำไปสู่ข้อสรุปเดียวกัน (effect ใหญ่) แต่ omega squared เป็นค่าประมาณที่ระมัดระวังกว่าและไม่เอนเอียง
ควรรายงานตัวไหน?
สำหรับวิทยานิพนธ์ส่วนใหญ่ eta squared เป็นที่ยอมรับและรายงานกันบ่อยกว่า แต่ถ้าอาจารย์หรือสาขาของคุณนิยม omega squared หรือถ้าคุณมีกลุ่มตัวอย่างเล็ก ให้ใช้ omega squared และระบุเหตุผล: "Omega squared ถูกคำนวณแทน eta squared เพื่อให้ค่าประมาณที่ไม่เอนเอียงของ effect size ประชากร เนื่องจากขนาดกลุ่มตัวอย่างค่อนข้างเล็ก"
คำถามที่พบบ่อย
ขั้นตอนถัดไป: การใช้ Effect Size ในวิทยานิพนธ์
การคำนวณ effect size เป็นขั้นตอนหนึ่ง การกระทำเหล่านี้จะทำให้การวิเคราะห์วิทยานิพนธ์ของคุณสมบูรณ์:
รายงาน effect size สำหรับการทดสอบ inferential ทุกตัว กลับไปดูบทผลการวิจัย t-test และ ANOVA ทุกตัวควรมี effect size ที่เกี่ยวข้อง เพิ่มตอนนี้โดยใช้สูตรจากคู่มือนี้
เปรียบเทียบ effect ของคุณกับงานวิจัยที่ตีพิมพ์ ค้นหา meta-analyses ในสาขาวิจัยของคุณ รายงานว่า effect size ของคุณเปรียบเทียบกับช่วงทั่วไปอย่างไร: "Effect ที่สังเกตได้ (d = 0.62) มากกว่า effect การทดลองเฉลี่ยที่รายงานใน meta-analysis ของ Lee และคณะ (2024) (d = 0.41) บ่งบอกว่าวิธีนี้อาจมีประสิทธิภาพเป็นพิเศษ"
ตีความ effect size ในบทอภิปราย นัยสำคัญทางสถิติตอบว่ามี effect หรือไม่ Effect size ตอบว่ามันมีความหมายหรือไม่ อภิปรายนัยสำคัญทางปฏิบัติของขนาด effect size ของคุณ Effect ใหญ่บ่งบอกว่าการทดลองของคุณพร้อมนำไปใช้ Effect เล็กบ่งบอกว่าต้องปรับปรุง
ใช้ effect size สำหรับ power analysis ในข้อเสนอแนะการวิจัยในอนาคต ส่วนข้อจำกัดของวิทยานิพนธ์ควรแนะนำขนาดกลุ่มตัวอย่างที่เหมาะสมสำหรับการศึกษาในอนาคต ใช้ effect size ที่สังเกตได้เพื่อคำนวณ n ที่ต้องการสำหรับ power ที่เพียงพอ (โดยทั่วไป 0.80) ถ้าการศึกษานำร่องของคุณพบ d = 0.5 แนะนำกลุ่มตัวอย่างในอนาคต n = 64 ต่อกลุ่ม (128 รวม) เพื่อให้ได้ 80% power
สร้างแม่แบบ Excel ที่ใช้ซ้ำได้ บันทึกเครื่องคำนวณ Cohen's d และ eta squared ของคุณเป็นแม่แบบ คุณจะใช้มันสำหรับการวิเคราะห์หลายครั้งตลอดวิทยานิพนธ์และโปรเจกต์วิจัยในอนาคต
ถ้าคุณทำงานกับข้อมูลแบบสอบถามสำหรับวิทยานิพนธ์ คู่มือฉบับสมบูรณ์ของเราเกี่ยวกับวิธีวิเคราะห์ข้อมูลแบบสอบถามใน Excel ครอบคลุม workflow ทั้งหมดตั้งแต่การเตรียมข้อมูลถึงการวิเคราะห์ทางสถิติ
สำหรับคำแนะนำเพิ่มเติมเกี่ยวกับการรายงานผลทางสถิติในรูปแบบ APA ดูคู่มือของเราเกี่ยวกับวิธีรายงานสถิติเชิงพรรณนาในรูปแบบ APA
ถ้าคุณต้องการกำหนดว่าควรทำการทดสอบทางสถิติอะไรก่อนคำนวณ effect size ให้ดูคู่มือการตัดสินใจของเราเกี่ยวกับt-test vs ANOVA ใน Excel