ANOVA ทางเดียว (การวิเคราะห์ความแปรปรวน) เป็นการทดสอบทางสถิติที่เปรียบเทียบค่าเฉลี่ยของสามกลุ่มอิสระขึ้นไปเพื่อกำหนดว่าค่าเฉลี่ยของกลุ่มอย่างน้อยหนึ่งกลุ่มแตกต่างอย่างมีนัยสำคัญจากกลุ่มอื่นหรือไม่ แม้ว่า Excel จะไม่แข็งแกร่งเท่า SPSS หรือ R สำหรับสถิติขั้นสูง แต่ก็จัดการ ANOVA ทางเดียวได้ดีผ่าน Data Analysis ToolPak
บทเรียนที่สมบูรณ์นี้จะแสดงให้คุณเห็นวิธีการคำนวณ ANOVA ทางเดียวใน Excel ทีละขั้นตอน รวมถึงการทดสอบสมมติฐาน การคำนวณ effect size และรูปแบบการรายงานผลแบบ APA สำหรับวิทยานิพนธ์หรือดุษฎีนิพนธ์ของคุณ
ANOVA ทางเดียวคืออะไร
ANOVA ทางเดียวทดสอบว่าค่าเฉลี่ยของสามกลุ่มอิสระขึ้นไปแตกต่างกันในตัวแปรตามแบบต่อเนื่องหรือไม่ "ทางเดียว" หมายความว่าคุณมี ตัวแปรอิสระหนึ่งตัว (factor) ที่มีหลายระดับ (กลุ่ม)
ตัวอย่างคำถามการวิจัย: "คะแนนความพึงพอใจของลูกค้าแตกต่างกันระหว่างสามกลุ่มอายุ (18-25, 26-40, 41+) หรือไม่"
- ตัวแปรอิสระ (Factor): กลุ่มอายุ (3 ระดับ)
- ตัวแปรตาม: คะแนนความพึงพอใจ (ต่อเนื่อง)
- สมมติฐานหลัก (H₀): ค่าเฉลี่ยของกลุ่มทั้งหมดเท่ากัน (μ₁ = μ₂ = μ₃)
- สมมติฐานรอง (H₁): ค่าเฉลี่ยของกลุ่มอย่างน้อยหนึ่งกลุ่มแตกต่างกัน
เมื่อไหร่ควรใช้ ANOVA กับ T-Test
ใช้ ANOVA ทางเดียว เมื่อเปรียบเทียบ สามกลุ่มขึ้นไป อย่าทำ t-tests หลายครั้งเพื่อเปรียบเทียบกลุ่มหลายกลุ่ม เพราะมันจะเพิ่มอัตราข้อผิดพลาดแบบ Type I ของคุณ
สำหรับคู่มือการตัดสินใจแบบสมบูรณ์ ดูที่: T-Test vs ANOVA ใน Excel: ควรใช้อันไหน
กฎการตัดสินใจอย่างรวดเร็ว:
- 2 กลุ่ม → ใช้ independent samples t-test
- 3+ กลุ่ม → ใช้ ANOVA ทางเดียว
ข้อกำหนดเบื้องต้น: เปิดใช้งาน Data Analysis ToolPak
ก่อนที่จะทำ ANOVA คุณต้องเปิดใช้งาน Analysis ToolPak add-in ของ Excel ก่อน
สำหรับคำแนะนำการติดตั้งโดยละเอียดสำหรับทั้ง Windows และ Mac ดูคู่มือของเรา: วิธีเปิดใช้งาน Data Analysis ใน Excel
ขั้นตอนอย่างรวดเร็วสำหรับ Windows:
- คลิก File → Options
- เลือก Add-ins จากเมนูด้านซ้าย
- ในกล่อง Manage ด้านล่าง เลือก Excel Add-ins และคลิก Go
- ติ๊กถูกที่กล่อง Analysis ToolPak
- คลิก OK
ปุ่ม Data Analysis จะปรากฏในแท็บ Data ภายใต้กลุ่ม Analysis
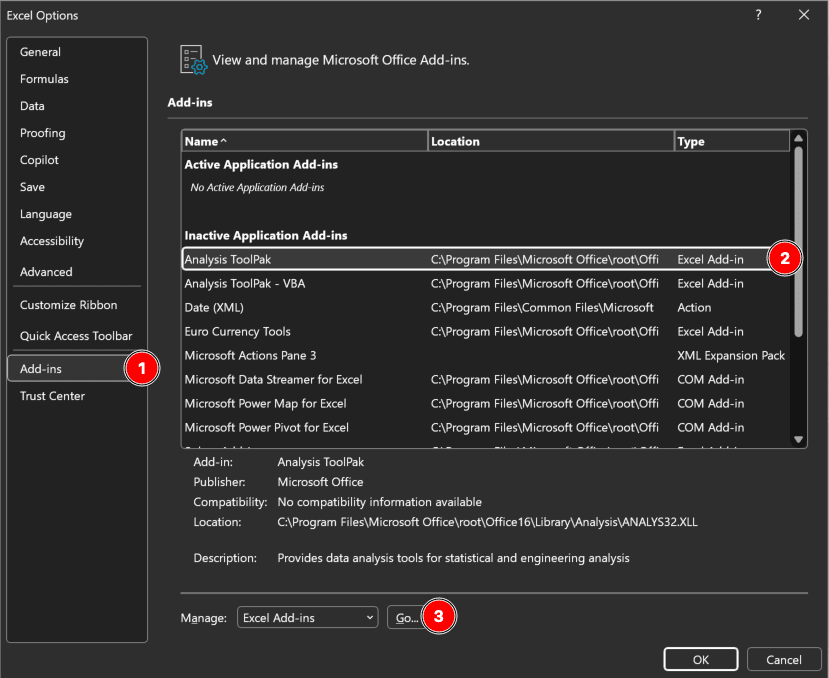 รูปที่ 1: กล่องโต้ตอบ Excel Add-ins ที่เปิดใช้งาน Analysis ToolPak (Windows)
รูปที่ 1: กล่องโต้ตอบ Excel Add-ins ที่เปิดใช้งาน Analysis ToolPak (Windows)
ผู้ใช้ Mac: ไปที่ Tools → Excel Add-ins แทน File → Options
ต้องการวิเคราะห์สถิติ?
เราสอนนักศึกษาและนักวิจัยวิเคราะห์ข้อมูลด้วย SPSS, Excel, R และ Amos
ติดต่อเราทีละขั้นตอน: วิธีคำนวณ ANOVA ทางเดียวใน Excel
เราจะใช้ข้อมูลตัวอย่างที่เปรียบเทียบคะแนนความพึงพอใจของลูกค้าระหว่างสามกลุ่มอายุ
ขั้นตอนที่ 1: จัดระเบียบข้อมูลของคุณ
จัดข้อมูลของคุณในคอลัมน์ โดยแต่ละคอลัมน์แทนกลุ่มหนึ่ง รวมแถวหัวข้อด้วยป้ายกำกับกลุ่ม
โครงสร้างข้อมูลตัวอย่าง:
| Age 18-25 | Age 26-40 | Age 41+ |
|---|---|---|
| 3.2 | 4.1 | 4.3 |
| 2.8 | 3.9 | 4.5 |
| 3.5 | 4.3 | 4.2 |
| 3.1 | 4.0 | 4.6 |
| 2.9 | 4.2 | 4.4 |
| 3.4 | 3.8 | 4.1 |
| 3.0 | 4.4 | 4.7 |
| 3.3 | 4.1 | 4.3 |
| 2.7 | 3.7 | 4.0 |
| 3.6 | 4.5 | 4.8 |
ตารางที่ 1: คะแนนความพึงพอใจของลูกค้าตามกลุ่มอายุ (มาตราวัด 1-5)
จุดสำคัญ:
- แต่ละคอลัมน์ = กลุ่มหนึ่ง (Age 18-25, Age 26-40, Age 41+)
- แต่ละแถว = ผู้ตอบหนึ่งคน
- ป้ายกำกับกลุ่มอยู่ในแถวที่ 1
- ข้อมูลตัวเลขเริ่มตั้งแต่แถวที่ 2
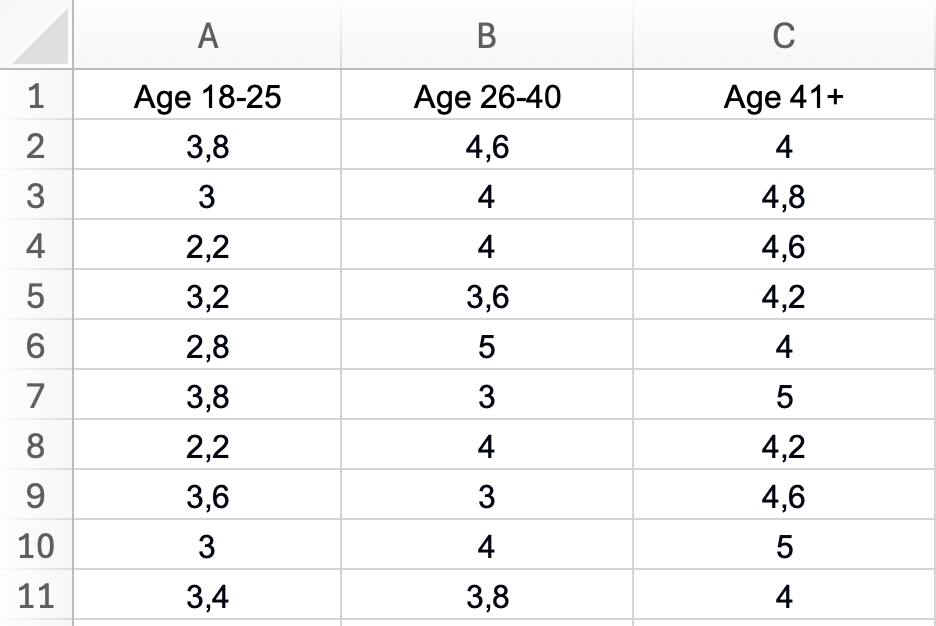 รูปที่ 2: การจัดวางข้อมูลที่ถูกต้องสำหรับ one-way ANOVA - แต่ละกลุ่มอายุในคอลัมน์แยกกันพร้อมหัวข้อที่อธิบาย
รูปที่ 2: การจัดวางข้อมูลที่ถูกต้องสำหรับ one-way ANOVA - แต่ละกลุ่มอายุในคอลัมน์แยกกันพร้อมหัวข้อที่อธิบาย
ขั้นตอนที่ 2: เข้าถึง Data Analysis
- คลิกแท็บ Data
- ในกลุ่ม Analysis (ด้านขวา) คลิก Data Analysis
- กล่องโต้ตอบที่มีเครื่องมือการวิเคราะห์จะปรากฏขึ้น
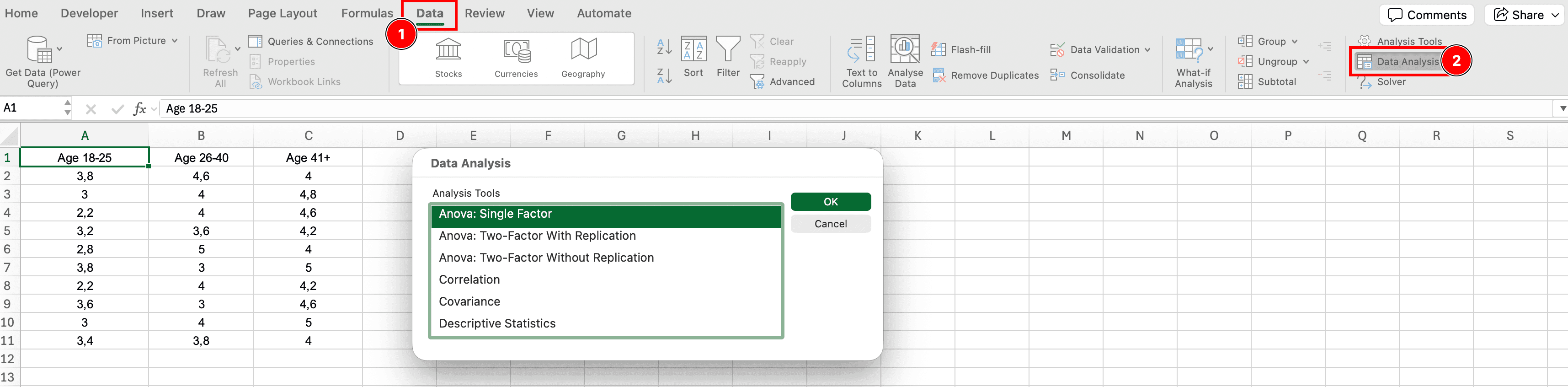 รูปที่ 3: ตำแหน่งปุ่ม Data Analysis ในแท็บ Data ของ Excel
รูปที่ 3: ตำแหน่งปุ่ม Data Analysis ในแท็บ Data ของ Excel
ขั้นตอนที่ 3: เลือก Anova: Single Factor
- ในกล่องโต้ตอบ Data Analysis เลื่อนลงและเลือก Anova: Single Factor
- คลิก OK
"Single Factor" หมายความว่าตัวแปรอิสระหนึ่งตัว (กลุ่มอายุ) สำหรับตัวแปรอิสระสองตัว คุณจะใช้ "Anova: Two-Factor"
ขั้นตอนที่ 4: ตั้งค่า ANOVA
กล่องโต้ตอบ Anova: Single Factor ปรากฏขึ้น ตั้งค่าเหล่านี้:
Input Range:
- คลิกไอคอนเครื่องหมายเลือกช่วง
- เลือก ข้อมูลทั้งหมด รวมทั้งหัวข้อ (เช่น: A1:C11)
- ตรวจสอบให้แน่ใจว่าคุณรวมทั้งป้ายกำกับและค่า
Grouped By:
- เลือก Columns (ข้อมูลถูกจัดระเบียบในคอลัมน์)
Labels in First Row:
- ติ๊กถูกที่กล่องนี้ (เพราะแถวที่ 1 มีหัวข้อกลุ่ม)
Alpha:
- ปล่อยไว้ที่ 0.05 (ระดับนัยสำคัญมาตรฐาน 95%)
Output Options:
- เลือก Output Range และคลิกเซลล์ (เช่น: E1)
- หรือเลือก New Worksheet เพื่อสร้างแผ่นงานแยก
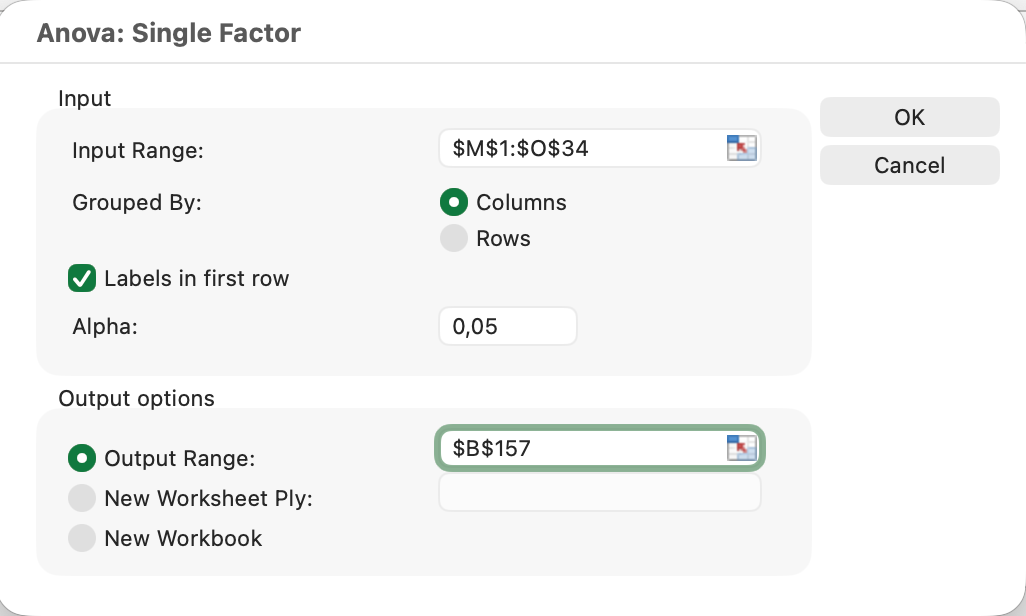 รูปที่ 4: การตั้งค่ากล่องโต้ตอบ Anova: Single Factor พร้อมสามกลุ่มอายุ
รูปที่ 4: การตั้งค่ากล่องโต้ตอบ Anova: Single Factor พร้อมสามกลุ่มอายุ
คลิก OK เพื่อสร้างผลลัพธ์
ขั้นตอนที่ 5: ตีความผลลัพธ์ ANOVA
Excel จะสร้างสองตาราง:
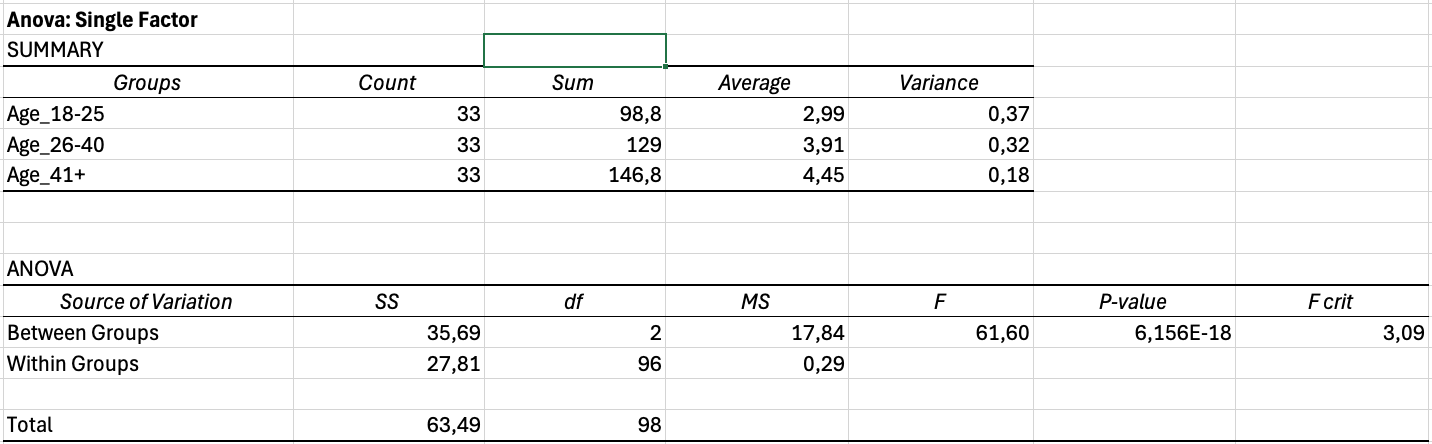 รูปที่ 5: ผลลัพธ์ ANOVA ของ Excel พร้อมสถิติเชิงพรรณนาและ F-test
รูปที่ 5: ผลลัพธ์ ANOVA ของ Excel พร้อมสถิติเชิงพรรณนาและ F-test
ตารางที่ 1: Summary (สถิติเชิงพรรณนา)
ตารางนี้แสดงสำหรับแต่ละกลุ่ม:
- Count = ขนาดตัวอย่าง (มีการสังเกตกี่ตัว)
- Sum = ผลรวมของค่าทั้งหมด
- Average = ค่าเฉลี่ยของกลุ่ม
- Variance = ความแปรปรวนของกลุ่ม
ตัวอย่างการตีความ:
- กลุ่มอายุ 18-25: M = 3.2, n = 30
- กลุ่มอายุ 26-40: M = 4.1, n = 30
- กลุ่มอายุ 41+: M = 4.3, n = 30
ตารางที่ 2: ANOVA (การทดสอบหลัก)
นี่คือตารางสำคัญสำหรับการทดสอบสมมติฐาน:
| Source of Variation | SS | df | MS | F | P-value | F crit |
|---|---|---|---|---|---|---|
| Between Groups | 31.44 | 2 | 15.72 | 61.60 | 0.001 | 3.10 |
| Within Groups | 22.23 | 87 | 0.26 | — | — | — |
| Total | 53.67 | 89 | — | — | — | — |
ตารางที่ 2: ตาราง ANOVA แสดงความแตกต่างอย่างมีนัยสำคัญระหว่างกลุ่ม (p < 0.001)
คำอธิบายคอลัมน์:
- SS (Sum of Squares): ความแปรปรวนทั้งหมดแบ่งเป็น "Between Groups" (ความแตกต่างระหว่างค่าเฉลี่ยของกลุ่ม) และ "Within Groups" (ความแตกต่างภายในแต่ละกลุ่ม)
- df (Degrees of Freedom): Between Groups = k - 1 (3 กลุ่ม - 1 = 2); Within Groups = N - k (90 - 3 = 87)
- MS (Mean Square): SS หารด้วย df
- F: สถิติการทดสอบ = MS Between Groups / MS Within Groups
- P-value: ความน่าจะเป็นที่จะได้ผลลัพธ์นี้ถ้าสมมติฐานหลักเป็นจริง
- F crit: ค่า F ในตารางสำหรับ alpha = 0.05
การตีความของคุณ:
ถ้า P-value < 0.05: ปฏิเสธสมมติฐานหลัก ค่าเฉลี่ยของกลุ่มอย่างน้อยหนึ่งกลุ่มแตกต่างอย่างมีนัยสำคัญ
ถ้า P-value ≥ 0.05: ไม่ปฏิเสธสมมติฐานหลัก ไม่มีความแตกต่างอย่างมีนัยสำคัญระหว่างกลุ่ม
ตัวอย่าง: F(2, 87) = 61.60, p < 0.001
นี่หมายความว่ามีความแตกต่างอย่างมีนัยสำคัญมากในความพึงพอใจระหว่างกลุ่มอายุ
การตรวจสอบสมมติฐาน ANOVA
ANOVA มีสมมติฐานหลักสามข้อที่ต้องเป็นไปตาม:
1. ความเป็นอิสระของการสังเกต
หมายความว่าอย่างไร: แต่ละการสังเกตต้องเป็นอิสระ คะแนนของคนหนึ่งไม่ควรมีอิทธิพลต่อคะแนนของอีกคนหนึ่ง
วิธีตรวจสอบ: ตรวจสอบการออกแบบการวิจัย:
- แต่ละผู้เข้าร่วมปรากฏในข้อมูลเพียงครั้งเดียว
- ผู้เข้าร่วมถูกกำหนดแบบสุ่มให้กับกลุ่ม (ถ้ามี)
- ไม่มีการวัดซ้ำ (บุคคลเดียวกันที่ถูกทดสอบหลายครั้ง)
ทำอะไรถ้าถูกละเมิด: ถ้าคุณมีการวัดซ้ำ ใช้ repeated measures ANOVA แทน
2. ความเป็นปกติของ Residuals
หมายความว่าอย่างไร: ตัวแปรตามควรมีการแจกแจงแบบปกติโดยประมาณในแต่ละกลุ่ม
วิธีตรวจสอบใน Excel:
วิธีที่ 1: Histograms (ดูเป็นภาพ รวดเร็ว)
- สร้าง histograms สำหรับแต่ละกลุ่ม
- มองหาการแจกแจงที่เป็นรูประฆังโดยประมาณ
- ความเบ้หรือค่าผิดปกติที่ชัดเจนเป็นสัญญาณเตือน
วิธีที่ 2: กฎเกณฑ์เชิงประจักษ์ (สำหรับ n > 30 ต่อกลุ่ม)
- ด้วยตัวอย่างขนาดใหญ่ (n > 30 ต่อกลุ่ม) ANOVA แข็งแกร่งต่อการละเมิดเล็กน้อย
- ตรวจสอบด้วยตาว่าการแจกแจงไม่เบ้มากเกินไป
ทำอะไรถ้าถูกละเมิด:
- แปลงข้อมูล (log, square root)
- ใช้การทดสอบ non-parametric (Kruskal-Wallis test)
- ด้วย n > 30 ต่อกลุ่มและขนาดกลุ่มเท่ากัน ANOVA มักจะโอเค
3. ความเท่ากันของความแปรปรวน (Homoscedasticity)
หมายความว่าอย่างไร: ความแปรปรวนของตัวแปรตามควรคล้ายกันในทุกกลุ่ม
วิธีตรวจสอบใน Excel:
F-max Test (ง่ายที่สุดสำหรับ Excel):
- จากตาราง ANOVA Summary จดความแปรปรวนของแต่ละกลุ่ม
- คำนวณอัตราส่วน F-max:
F-max = ความแปรปรวนที่ใหญ่ที่สุด / ความแปรปรวนที่เล็กที่สุด
กฎการตัดสินใจ:
- F-max < 3: ความเท่ากันของความแปรปรวนเป็นไปตาม
- F-max > 3 แต่ < 10: พื้นที่เทา ดำเนินการต่อด้วยความระมัดระวังถ้าขนาดตัวอย่างเท่ากัน
- F-max > 10: การละเมิดอย่างรุนแรง พิจารณาใช้ Welch's ANOVA
ตัวอย่าง:
- ความแปรปรวนกลุ่ม 18-25: 0.64
- ความแปรปรวนกลุ่ม 26-40: 0.81
- ความแปรปรวนกลุ่ม 41+: 0.36
F-max = 0.81 / 0.36 = 2.25 (< 3 ดังนั้นโอเค)
ทำอะไรถ้าถูกละเมิด:
- แปลงข้อมูล (log, square root)
- ใช้ Welch's ANOVA (ต้องใช้ SPSS หรือ R)
- ถ้าขนาดตัวอย่างเท่ากันและ F-max < 10 ANOVA มักจะแข็งแกร่ง

รูปที่ 6: รายการตรวจสอบสมมติฐาน ANOVA - ตรวจสอบทั้งสามข้อก่อนที่จะตีความผลลัพธ์
การคำนวณ Effect Size (Eta Squared)
ค่า p บอกคุณว่ามีความแตกต่างหรือไม่ แต่ effect size บอกคุณว่าความแตกต่างนั้น ใหญ่แค่ไหน
ทำไม Effect Size ถึงสำคัญ
นัยสำคัญทางสถิติ ≠ นัยสำคัญเชิงปฏิบัติ
ตัวอย่าง: ด้วย n = 1000 ความแตกต่างเล็กน้อยสามารถมีนัยสำคัญทางสถิติ (p < 0.05) แต่ไม่มีนัยสำคัญเชิงปฏิบัติ
Eta squared (η²) วัดสัดส่วนของความแปรปรวนในตัวแปรตามที่อธิบายโดยการเป็นสมาชิกกลุ่ม
วิธีคำนวณ Eta Squared ใน Excel
สูตร:
η² = SS Between Groups / SS Total
ขั้นตอน:
- จากตาราง ANOVA หา:
- SS Between Groups (เช่น: 31.44)
- SS Total (เช่น: 53.67)
- ในเซลล์ว่าง ใส่:
=31.44/53.67 - ผลลัพธ์คือ eta squared: η² = 0.59
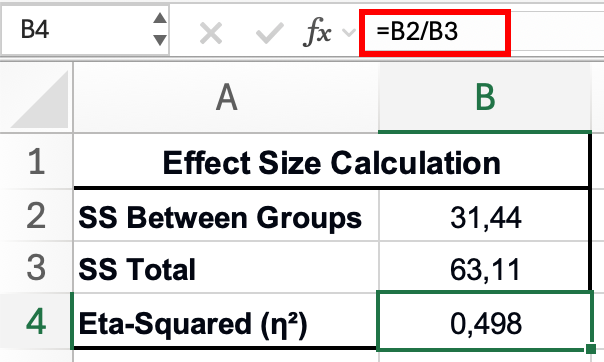 รูปที่ 7: การคำนวณ eta-squared (effect size) จากผลลัพธ์ ANOVA
รูปที่ 7: การคำนวณ eta-squared (effect size) จากผลลัพธ์ ANOVA
การตีความ Eta Squared
| Effect Size | ค่า η² | การตีความ |
|---|---|---|
| เล็ก | 0.01 - 0.06 | การเป็นสมาชิกกลุ่มอธิบาย 1-6% ของความแปรปรวน |
| กลาง | 0.06 - 0.14 | การเป็นสมาชิกกลุ่มอธิบาย 6-14% ของความแปรปรวน |
| ใหญ่ | ≥ 0.14 | การเป็นสมาชิกกลุ่มอธิบาย 14%+ ของความแปรปรวน |
ตารางที่ 3: แนวทางการตีความ eta squared (Cohen, 1988)
ตัวอย่างของเรา: η² = 0.59 หมายความว่ากลุ่มอายุอธิบาย 59% ของความแปรปรวนในความพึงพอใจ นี่เป็น effect size ที่ใหญ่มาก
Post-Hoc Tests: กลุ่มไหนที่แตกต่างกัน
ANOVA บอกคุณว่ากลุ่ม มี ความแตกต่าง ไม่ได้บอก กลุ่มไหน ที่แตกต่างกัน
ถ้า ANOVA มีนัยสำคัญ (p < 0.05) คุณต้องทำ post-hoc tests เพื่อระบุคู่เฉพาะที่แตกต่างกัน
Pairwise T-Tests กับ Bonferroni Correction
เนื่องจาก Excel ไม่มีเครื่องมือ post-hoc ที่สร้างมา ใช้ pairwise t-tests กับ Bonferroni correction เพื่อควบคุมอัตราข้อผิดพลาด
Bonferroni Correction:
Adjusted alpha = 0.05 / จำนวนการเปรียบเทียบ
สำหรับ 3 กลุ่ม:
- จำนวนการเปรียบเทียบ = 3 (กลุ่ม 1 vs 2, กลุ่ม 1 vs 3, กลุ่ม 2 vs 3)
- Adjusted alpha = 0.05 / 3 = 0.017
กฎการตัดสินใจ: การเปรียบเทียบคู่มีนัยสำคัญเฉพาะถ้า p < 0.017 (ไม่ใช่ 0.05)
วิธีทำ Pairwise T-Tests ใน Excel
สำหรับแต่ละคู่กลุ่ม:
- Data Analysis → t-Test: Two-Sample Assuming Equal Variances
- Variable 1 Range: เลือกข้อมูลกลุ่ม 1 (ไม่มีหัวข้อ)
- Variable 2 Range: เลือกข้อมูลกลุ่ม 2 (ไม่มีหัวข้อ)
- Hypothesized Mean Difference: 0
- Alpha: 0.05 (แต่เปรียบเทียบกับ 0.017)
- คลิก OK
ทำซ้ำสำหรับทั้ง 3 คู่:
- Age 18-25 vs Age 26-40
- Age 18-25 vs Age 41+
- Age 26-40 vs Age 41+
ตัวอย่างผลลัพธ์ Post-Hoc
| Comparison | Mean Difference | P-value | Significant? (p < 0.017) |
|---|---|---|---|
| 18-25 vs 26-40 | -0.9 | 0.004 | ใช่ |
| 18-25 vs 41+ | -1.1 | 0.001 | ใช่ |
| 26-40 vs 41+ | -0.2 | 0.234 | ไม่ใช่ |
ตารางที่ 4: ผลลัพธ์การเปรียบเทียบคู่ post-hoc พร้อม Bonferroni correction
การตีความ:
- กลุ่ม 18-25 ได้คะแนน ต่ำกว่าอย่างมีนัยสำคัญ กว่ากลุ่ม 26-40 (p = 0.004) และ 41+ (p = 0.001)
- กลุ่ม 26-40 และ 41+ ไม่แตกต่างกันอย่างมีนัยสำคัญ (p = 0.234)
การรายงานผลลัพธ์ ANOVA ในรูปแบบ APA
รายงานผลลัพธ์ ANOVA ในรูปแบบ APA มาตรฐานสำหรับวิทยานิพนธ์/ดุษฎีนิพนธ์ของคุณ
1. สถิติเชิงพรรณนา
ตารางที่ 5: สถิติเชิงพรรณนาสำหรับคะแนนความพึงพอใจตามกลุ่มอายุ
| Age Group | n | M | SD |
|---|---|---|---|
| 18-25 years | 30 | 3.2 | 0.8 |
| 26-40 years | 30 | 4.1 | 0.7 |
| 41+ years | 30 | 4.3 | 0.6 |
หมายเหตุ: n = ขนาดตัวอย่าง; M = ค่าเฉลี่ย; SD = ส่วนเบี่ยงเบนมาตรฐาน
2. ผลลัพธ์ ANOVA หลัก
ทำ one-way ANOVA เพื่อเปรียบเทียบคะแนนความพึงพอใจระหว่างสามกลุ่มอายุ (18-25, 26-40, 41+) สมมติฐานความเท่ากันของความแปรปรวนเป็นไปตาม (F-max = 2.25) ANOVA เผยให้เห็นความแตกต่างอย่างมีนัยสำคัญในคะแนนความพึงพอใจระหว่างกลุ่มอายุ, F(2, 87) = 61.60, p < .001, η² = 0.59 บ่งชี้ถึง effect size ที่ใหญ่มาก
องค์ประกอบสำคัญ:
- รายงานสถิติ F พร้อมองศาอิสระ: F(df between, df within) = F value
- รายงานค่า p (ถ้า p < 0.001 รายงานเป็น p < .001)
- รวม effect size (η²)
- ปัดเศษ F เป็น 2 ทศนิยม, p เป็น 3 ทศนิยม, η² เป็น 2 ทศนิยม
3. ผลลัพธ์ Post-Hoc (ถ้า ANOVA มีนัยสำคัญ)
การเปรียบเทียบ post-hoc โดยใช้ Bonferroni correction บ่งชี้ว่ากลุ่มอายุ 18-25 (M = 3.2, SD = 0.8) ได้คะแนนต่ำกว่ากลุ่มอายุ 26-40 (M = 4.1, SD = 0.7, p = .004) และกลุ่มอายุ 41+ (M = 4.3, SD = 0.6, p = .001) อย่างมีนัยสำคัญ กลุ่ม 26-40 และ 41+ ไม่แตกต่างกันอย่างมีนัยสำคัญ (p = .234)
ตัวอย่างแบบสมบูรณ์ (ส่วนผลลัพธ์)
ความแตกต่างในความพึงพอใจระหว่างกลุ่มอายุ
สถิติเชิงพรรณนาแสดงในตารางที่ 5 ทำ one-way ANOVA เพื่อเปรียบเทียบคะแนนความพึงพอใจระหว่างสามกลุ่มอายุ (18-25, 26-40, 41+) สมมติฐานความเท่ากันของความแปรปรวนเป็นไปตาม (F-max = 2.25) ANOVA เผยให้เห็นความแตกต่างอย่างมีนัยสำคัญในคะแนนความพึงพอใจระหว่างกลุ่มอายุ, F(2, 87) = 61.60, p < .001, η² = 0.59 บ่งชี้ถึง effect size ที่ใหญ่มาก
การเปรียบเทียบคู่ post-hoc โดยใช้ Bonferroni correction เผยให้เห็นว่ากลุ่มอายุ 18-25 (M = 3.2, SD = 0.8) ได้คะแนนต่ำกว่ากลุ่มอายุ 26-40 (M = 4.1, SD = 0.7, p = .004) และกลุ่มอายุ 41+ (M = 4.3, SD = 0.6, p = .001) อย่างมีนัยสำคัญ กลุ่ม 26-40 และ 41+ ไม่แตกต่างกันอย่างมีนัยสำคัญ (p = .234) ผลลัพธ์เหล่านี้บ่งชี้ว่าความพึงพอใจของลูกค้าเพิ่มขึ้นตามอายุ โดยลูกค้าที่อายุน้อยกว่า (18-25) รายงานความพึงพอใจที่ต่ำกว่ากลุ่มอายุที่มากกว่า
ต้องการวิเคราะห์สถิติ?
เราสอนนักศึกษาและนักวิจัยวิเคราะห์ข้อมูลด้วย SPSS, Excel, R และ Amos
ติดต่อเราข้อผิดพลาด ANOVA ทั่วไปที่ควรหลีกเลี่ยง
1. ทำ multiple t-tests แทน ANOVA
- ✗ ผิด: ทำ t-tests สำหรับคู่ทั้งหมดโดยไม่มี correction
- ✓ ถูก: ใช้ ANOVA ก่อน จากนั้น post-hoc tests
2. ไม่เช็คสมมติฐาน
- ✗ ผิด: ทำ ANOVA โดยไม่มีการตรวจสอบ
- ✓ ถูก: ทดสอบความเป็นปกติและความเท่ากันของความแปรปรวน
3. รายงานเฉพาะค่า p
- ✗ ผิด: "กลุ่มแตกต่างกันอย่างมีนัยสำคัญ (p < .05)"
- ✓ ถูก: รายงานสถิติ F, องศาอิสระ, ค่า p และ effect size
4. หยุดหลังจาก ANOVA มีนัยสำคัญ
- ✗ ผิด: สรุป "กลุ่มแตกต่างกัน" โดยไม่ระบุคู่ไหน
- ✓ ถูก: ทำ post-hoc tests เพื่อระบุความแตกต่างเฉพาะ
5. ใช้ ANOVA สำหรับสองกลุ่ม
- ✗ ผิด: ANOVA กับ 2 กลุ่ม
- ✓ ถูก: ใช้ independent samples t-test สำหรับ 2 กลุ่ม
การแก้ไขปัญหาทั่วไป
"ปุ่ม Data Analysis หายไป"
- วิธีแก้: เปิดใช้งาน Analysis ToolPak (ดูส่วนข้อกำหนดเบื้องต้น)
"Input Range มีข้อมูลที่ไม่ใช่ตัวเลข"
- วิธีแก้: ตรวจสอบให้แน่ใจว่าเซลล์ข้อมูลทั้งหมดมีเฉพาะตัวเลข ไม่มีข้อความ
- ลบเซลล์ว่างใดๆ ออกจากคอลัมน์ข้อมูล
"สถิติ F เล็กมาก (ใกล้ 1)"
- การตีความ: ค่าเฉลี่ยของกลุ่มคล้ายกัน ไม่มีความแตกต่างอย่างมีนัยสำคัญที่คาดหวัง
- ตรวจสอบว่าคุณเลือกช่วงข้อมูลที่ถูกต้องหรือไม่
"ค่า p ปรากฏเป็น scientific notation (1.2E-05)"
- การตีความ: นี่หมายความว่า p = 0.000012 ซึ่งเป็น < 0.001 (มีนัยสำคัญมาก)
- รายงานเป็น p < .001 ในรูปแบบ APA
"ความแปรปรวนไม่เท่ากันมาก (F-max > 10)"
- วิธีแก้ 1: แปลงข้อมูล (logarithmic หรือ square root transformation)
- วิธีแก้ 2: ใช้ Welch's ANOVA (ต้องใช้ R หรือ SPSS)
- วิธีแก้ 3: รายงานการละเมิดและดำเนินการต่อด้วยความระมัดระวังถ้าขนาดตัวอย่างเท่ากัน
ขั้นตอนถัดไป: นอกเหนือจาก One-Way ANOVA
หมายเหตุ: เทคนิค ANOVA ขั้นสูงต่อไปนี้ต้องใช้ software สถิติเช่น SPSS หรือ R (Data Analysis ToolPak ของ Excel รองรับเฉพาะ one-way ANOVA)
ถ้าคุณมีตัวแปรอิสระสองตัว:
- ใช้ two-way ANOVA เพื่อทดสอบ main effects และ interactions
ถ้าคุณมีการวัดซ้ำ:
- ใช้ repeated measures ANOVA (ผู้เข้าร่วมคนเดียวกันที่ถูกทดสอบหลายครั้ง)
ถ้าสมมติฐานถูกละเมิดอย่างรุนแรง:
- ใช้ Kruskal-Wallis test (ทางเลือก non-parametric)
สำหรับขั้นตอนการวิเคราะห์แบบสอบถามแบบสมบูรณ์:
- ดูคู่มือของเรา: วิธีวิเคราะห์ข้อมูลแบบสอบถามใน Excel: คู่มือสมบูรณ์
คำถามที่พบบ่อย
สรุป
One-way ANOVA ใน Excel ทำได้ง่ายโดยใช้ Data Analysis ToolPak:
- จัดระเบียบข้อมูล ในคอลัมน์ (หนึ่งคอลัมน์ต่อกลุ่ม)
- ทำ Anova: Single Factor ผ่าน Data Analysis
- เช็คสมมติฐาน (ความเป็นอิสระ, ความเป็นปกติ, ความเท่ากันของความแปรปรวน)
- ตีความผลลัพธ์ (สถิติ F และค่า p)
- คำนวณ effect size (eta-squared)
- ทำ post-hoc tests (Bonferroni correction) ถ้ามีนัยสำคัญ
- รายงานในรูปแบบ APA พร้อมสถิติเชิงพรรณนา
สิ่งสำคัญที่ต้องจำ: ANOVA บอกคุณว่ากลุ่ม มี ความแตกต่าง Post-hoc tests บอกคุณ กลุ่มไหน ที่แตกต่างกัน รายงานทั้งนัยสำคัญทางสถิติ (ค่า p) และนัยสำคัญเชิงปฏิบัติ (effect size) เสมอ
สำหรับการเปรียบเทียบเฉพาะสองกลุ่ม ใช้ T-Test ใน Excel: คู่มือสมบูรณ์ เพื่อตัดสินใจระหว่าง t-test และ ANOVA ดูที่ T-Test vs ANOVA: ควรใช้การทดสอบไหน