In this lesson, we will draw a comparison between the population vs. sample standard deviation formula and how to calculate the equations by hand.
The standard deviation requires us to know the average for the population or sample we measure. We are going to learn how to calculate the mean (average) for a set of values as well.
And if you manage to follow till the end, I have a bonus for you. I will show you how to extract variance from the standard deviation using one simple formula. Are you with me?
Lesson Outcome
Here is a summary of what you will learn in the next minutes:
- What is sample standard deviation, and when to use it in research?
- How to calculate the mean for a set of numbers.
- How to calculate the standard deviation sample formula by hand.
- How to extract variance from standard deviation.
Now, we will do a bit of hands-on math in this statistics lesson, but don’t worry. I’ll keep everything fun and easy! Without further ado, let’s get started.
Standard Deviation In A Nutshell
Standard deviation measures how dispersed the scores in a dataset are relative to the average of the scores. In other words, standard deviation measure the spread of a group of data points relative to the mean. The more spread they are, the higher the standard deviation.
To make sure we grasp this concept, think of the following two groups of numbers:
2, 3, 4 and 2, 4, 6.
Now, let me ask you: which set of numbers do you think has a greater standard deviation?
You are right: the second group consists of the numbers 2, 4, and 6. But why? Let’s compare these groups using a number line.

Aha! The standard deviation for the second group of numbers (2, 4, 6) must be higher because the values on the number line are more spread. In contrast, the numbers in the first group (2, 3, 4) are closer together; therefore, the standard deviation must be lower.
But how do we prove we are right? After all, a data set can have hundreds or even thousands of values.
Well, as you probably guessed, by using the standard deviation equation.
Before we get down to practicing our math skills, keep in mind that there are two equations for standard deviation, respectively:
- The population standard deviation formula calculates the standard deviation for an entire population and requires the population mean to be known.
- The sample standard deviation formula is used to compute the standard deviation for a population sample and requires the sample mean to be known.
Here is a side-by-side comparison between the two formulas, with the differences highlighted in red.
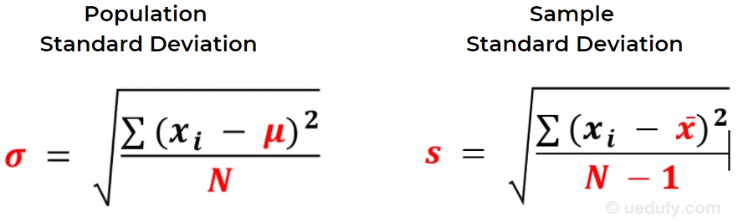
As you can see, the equation for population standard deviation is represented by the lowercase Greek letter Sigma σ while the sample standard deviation formula is by the letter s.
From a mathematics point of you, both sample and population standard deviation equations are calculated pretty much the same, with the exception of a few minor differences in notation and calculus which we will cover in detail next.
Population Standard Deviation Formula
As the name implies, the following equation is used to calculate the standard deviation for a given population.
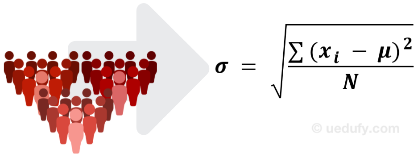
Where:
σ = symbol for population standard deviation
Σ = sum of the following terms
xi = every point in the dataset (observation or member of the population).
μ= population mean
N = the number of values in the population
Now let’s put everything together. This is how you read the population standard deviation formula: standard deviation (σ) equals the square root of the sum of (Σ) all the squared differences between every point xi in the dataset and the population mean (μ), divided by all the values in the set (N).
Next, let’s calculate the standard deviation for the set of numbers 3,4, and 5 using the population standard deviation formula.
Step 1: Find the mean (μ)
To find the mean of all members in a population, simply calculate the sum of all their values and then divide the sum by the number of values in the dataset. Here is the mean for the set of numbers 3, 4, and 5.
\mu=\frac{3+4+5}{3}=\frac{12}{3}=4TIP: When a set of numbers is equally spaced apart, the mean will be the number in the middle. For example, for the set of numbers, e.g., 2, 5, 7, 9, 12 the mean is 7.
Step 2: Calculate the standard deviation formula for the population
\sigma=\sqrt{\frac{\sum\left(x_{i}-\mu\right)^{2}}{N}}For the set of numbers 3, 4, and 5, every point xi = x3, x4, x5, the mean μ = 4 as calculated above, and the population N = 3 (as we have three values in the dataset). Let’s input these numbers in the population standard deviation equation:
\sigma=\sqrt{\frac{(3-4)^{2}+(4-4)^{2}+(5-4)^{2}}{3}}Step 3: Calculate the sum of all points
\sigma=\sqrt{\frac{1+0+1}{3}}Step 4: Solve the square root
\sigma=\sqrt{\frac{2}{3}}=\sqrt{0.66}=0.81The population standard deviation for the set of numbers 3, 4, and 5 is 0.81. Awesome!
PRACTICE: Using the population standard deviation formula and following the example above, calculate the standard deviation for the set of numbers 2, 4, and 6. Is the standard deviation higher or lower than 0.81?
Pretty simple right? But there is an issue with samples. While a population average remains the same (we always calculate the mean for ALL the members of the population), a sample can differ from one to another.
For example, if we close our eyes and take a few random samples consisting of 5 numbers from a bowl of one hundred numbers, every sample will likely contain different numbers. Therefore, the sample means will also differ between samples. Right?
So how do we make sure the sample we take is representative of the population from where it was sampled from? Say hello to another statistical term called the standard error. We won’t cover standard error since the article I linked above contains everything you need to know about it
Sample Standard Deviation Formula
But what happens when we don’t have access to the whole population but a sample of it to calculate the mean. This is often the case in social research and luckily for us, the sample standard deviation formula is not very different from the one used for the population.
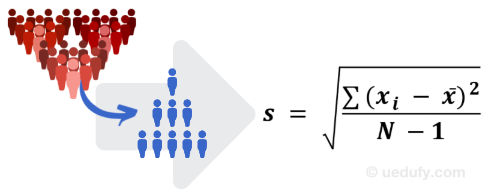
Where:
s = symbol for sample standard deviation
Σ = sum of the following terms
xi = every point in the dataset (observation or member of the population).
x̄ = sample mean
N-1 = the number of values in the sample (N) minus 1.
And this is how we read the above equation: sample standard deviation (s) is equal to the square root of the sum of (Σ) the squared differences between every data point (xi) in the sample and the sample mean (x̄), divided by population N – 1.
Is pretty easy to spot the difference between population and sample standard deviation formulas. One obvious difference is the notation for the sample mean x̄ as opposed to the population mean μ. Another difference is that we divide everything to N – 1.
The math for sample standard deviation is pretty much the same, but let’s do it anyway. This time we will use the second set of values from our number line: 2, 4, and 6.
Step 1: Calculate the sample mean (x̄)
This step is pretty much the same as finding the population average in the previous example. The sample mean for the set of numbers 2, 4, and 6 is 4. Here’s the proof:
\bar{x}=\frac{2+4+6}{3}=\frac{12}{3}=4Step 2: Calculate the sample standard deviation formula
s=\sqrt{\frac{\sum\left(x_{i}-\bar{x}\right)^{2}}{N-1}}Next, input the values in the sample standard deviation equation:
s=\sqrt{\frac{(2-4)^{2}+(4-4)^{2}+(6-4)^{2}}{3-1}}Step 3: Solve the square root
The sample standard deviation for the set of numbers 2, 4, and 6 is 2. We did it!
PRACTICE: Using the sample standard deviation formula and following the example above, calculate the standard deviation for the set of numbers 2, 5, 7, 9, and 12. To make it easier for you, the mean is 7.
Standard Deviation vs. Variance Relationship
And if we discussed standard deviation, we have to touch on another statistics term called variance. If the standard deviation is showing us how dispersed a group of numbers are from the mean, variance is giving us an average of how far each point in a dataset is relative to the mean.
The standard deviation and variance relationship becomes clear when looking at how variance is calculated. If we know the standard deviation for population or sample, all we need to do is to square it to find the variance.
\sigma^{2}={\frac{\sum\left(x_{i}-\mu\right)^{2}}{N}}For example, the population standard deviation result we calculated earlier is σ = 0.81, so we can calculate the population variance from it:
0.812 = 0.6561
Voila, the variance for the set of numbers 3, 4, and 5 is 0.6561.
The same can be done to calculate the variance for the sample using the following equation:
s^{2}={\frac{\sum\left(x_{i}-\bar{x}\right)^{2}}{N-1}}So to find the variance for the sample we calculated earlier all we need is to square the sample standard deviation, respectively:
s2 = 22 = 4
And if you managed to follow me this far, kudos! You are on the path to becoming a great researcher. Next, let us learn how to calculate the standard deviation with Excel for both population and sample using the equations we discussed so far.
Before you leave, here are the main points you should stick with you from this lesson.
Key Takeaway
- Standard deviation measures how dispersed a group of values are from their mean.
- Standard deviation is calculated using two equations, depending on if we evaluate a population or a sample.
- Both standard deviation and variance measure the dispersion of values in a distribution.
- Variance is not the same as standard deviation
- Variance can be easily calculated by squaring the standard deviation.
If you found this lesson useful, please share it with your university colleagues and friends. And if you think I can improve this article further, drop me a message. Your input will be highly appreciated!
Cite this article on your website or research paper:
[citationic]
References
Diez D.M., Cetinkaya-Rundel M., Barr C.D. OpenIntro: Statistics (4th Ed). 2019
Field, A. (2018). Discovering statistics using IBM SPSS statistics (5th edition). Sage: Thousand Oaks, CA.

