In this statistics lab, we will learn how to run mediation analysis in SPSS and interpret mediation analysis results so that you know precisely where to look when writing your mediation analysis report in your research paper.
This lesson will present two methods of conducting a mediation analysis.
The first method uses the default statistical tools available in any SPSS installation but requires more steps to accomplish the analysis. In the second method, I will show a simpler way to run mediation in SPSS using the PROCESS macro add-on.
Learning Outcomes
Upon completing this statistics lesson, you will learn the following:
- What is mediation analysis in statistical research?
- How to run mediation analysis in SPSS using two methods.
- How to estimate the indirect effect using the Sobel Test.
- How to calculate the point effect in mediation analysis.
- How to interpret mediation analysis in SPSS.
A sample SPSS dataset for mediation analysis will be provided so that you can practice this lab step-by-step on your computer.
What is Mediation in Research?
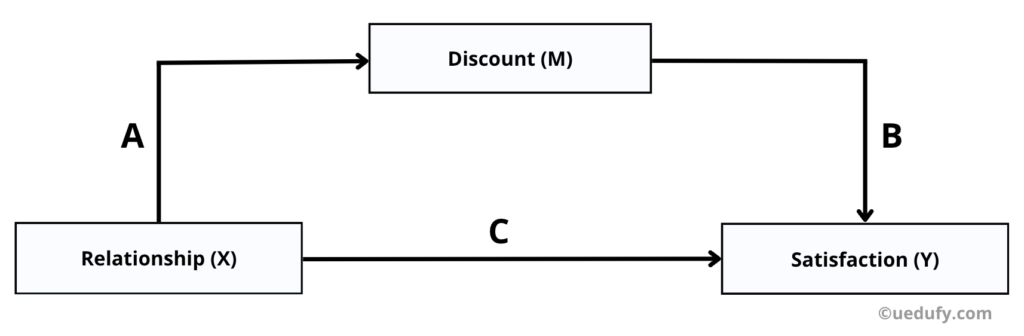
Mediation analysis enables us to investigate the effect of one or more independent variables (predictor) on a dependent variable (outcome) via a third variable called a mediator or intervening variable.
In contrast to moderation analysis, where the moderator variable interacts with the independent and dependent variables, mediation analysis involves positioning the mediator variable between the independent and dependent variables.

Where:
- Path A: The effect of the Independent Variable (X) on the Mediator Variable (M).
- Path B: The effect of the Mediator Variable (M) on the Dependent Variable (Y).
- Path C: The direct effect of the Independent Variable (X) on the Dependent Variable (Y).
In mediation analysis, our goal is to test if there is any statistical significance for the indirect effect and estimate the point effect using the Unstandardized Coefficient Beta and Standard Error for paths A and B.
An important takeaway is that mediation is correlational. In other words, all the variables in your mediation analysis must have a relationship between them. For instance, if there is no relationship between X and Y variables, there is nothing we can mediate. Makes sense?
However, correlation does not imply a cause and effect. That is what you must find out by making causal inferences between variables. And if your predictions are right, it confirms that your theory is valid.
In many cases, students often confuse mediation with moderation analysis. Before deciding if mediation analysis suits your model, I recommend first understanding the differences between mediator vs. moderator variables.
Example of Mediation Analysis
Let’s assume that we want to investigate a research hypothesis stating that discounts could mediate the effect between relationship and satisfaction variables.
In this example, “relationship” is the independent variable (X), “satisfaction” is the dependent variable (Y), and “discounts” is the mediator variable (M).
Before we start, I recommend you write down the notation for each variable, as we will use that in our mediation analysis from now on.
| Variable name | Variable type | Notation |
| Relationship | Independent variable | X |
| Satisfaction | Dependent variable | Y |
| Discounts | Mediator variable | M |
Our objective in this analysis is to test the statistical significance of the indirect effect (paths A * B).
If you want to follow along, I suggest downloading the sample dataset from the link below:
This SPSS data file contains dummy values and should be used for educational purposes only.
Method 1: How to run Mediation Analysis in SPSS
The first method we will use today requires more steps but is a great way of understanding how mediation analysis in SPSS works. Assuming you have already downloaded the sample data set from the link above, double-click on it to import it into SPSS.
- Estimate the total effect between X and Y variables.
First, we need to check the total effect of the X and Y variables. There is no point in conducting a mediation analysis if we find no statistical significance here. We can check the total effect between X and Y using a simple linear regression in SPSS.
In the SPSS top menu, navigate to Analyze → Regression → Linear.
From the left box, move the Relationship variable to the Dependent block, and the Satisfaction variable to the Independent block on the left by using the arrow buttons in between the blocks.
Press the OK button to proceed with the linear regression between X and Y. On the output window, let’s check the p-value in the Coefficients table, Sig. column. As you can see, the p-value is ≤ 0.05 therefore the total effect is significant (0.000).
- Estimate the direct effect of X on M.
Now, let’s estimate the direct effect of X on M to find the Beta coefficient and Standard Error for path A. This is an essential requirement for calculating the indirect effect later.
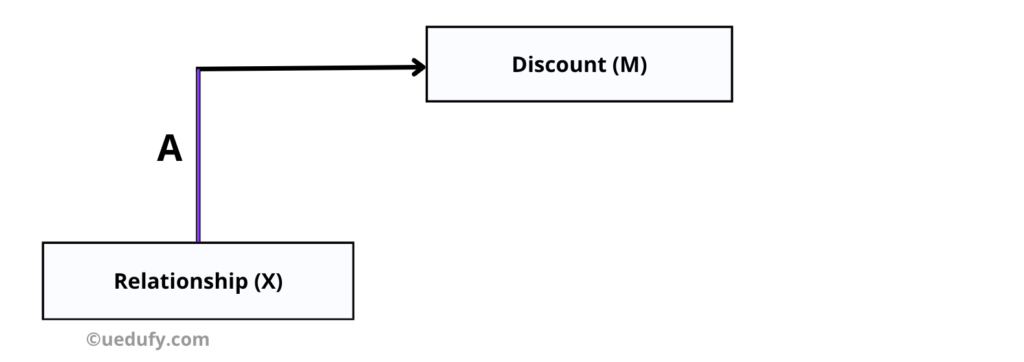
Again, this is done by using simple linear regression. Go to Analyze → Regression → Linear. Press the Reset button to clear the previous inputs and add the Discount variable to the Dependent block and the Relationship variable to the Independent block.
Press OK to proceed with the regression analysis.
On the output window, go straight to the Coefficient table. Here we can see that the effect of X on M is significant (p-value 0.000). What we really need from here is the Unstandardized Coefficient Beta weight (.413) and Std. Error (.084). Take note of these values for path A as we will need them in a moment.
- Estimate the direct effect of X and M on Y
In this step, we will estimate the direct effect between X and Y and M and Y to find the unstandardized beta and standard error coefficients for paths B and C.
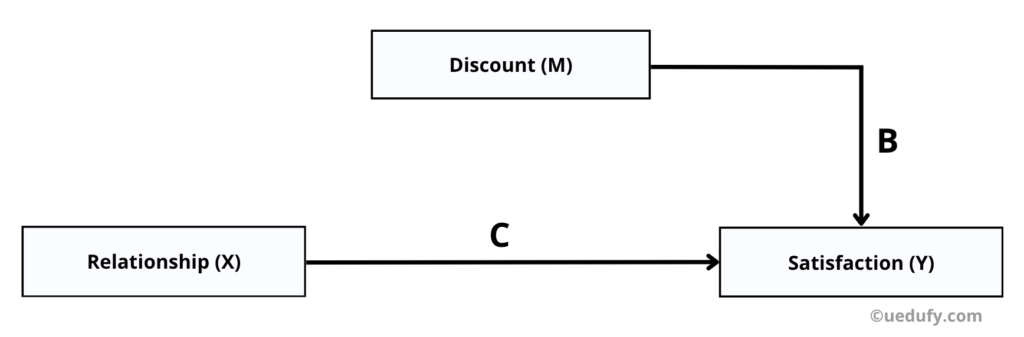
Since we are using two predictors (X and M) this time, we will use multiple linear regression.
Go to Analyze → Regression → Linear. Press the Reset button to clear the previous inputs.
Add the Satisfaction variable into the Dependent block and both Relationship and Discounts into the Independent block.
Press OK to proceed with multiple linear regression analysis.
On the Output window, go straight to the coefficients table to get the last piece of information we need to calculate the indirect effect for our example. Write down the value for Unstandardized Coefficient Beta (.733) and Std. Error (.043).
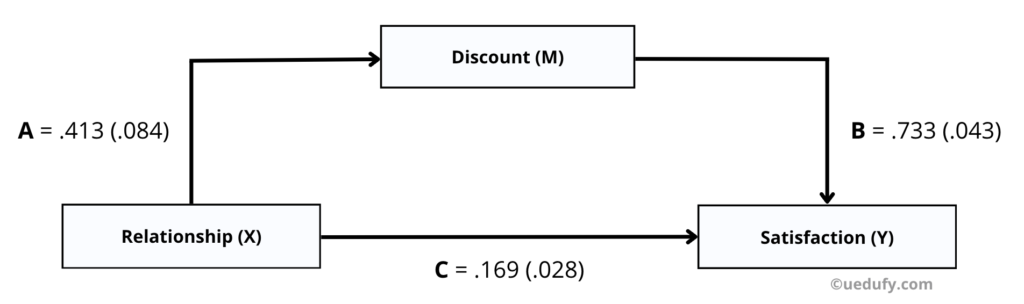
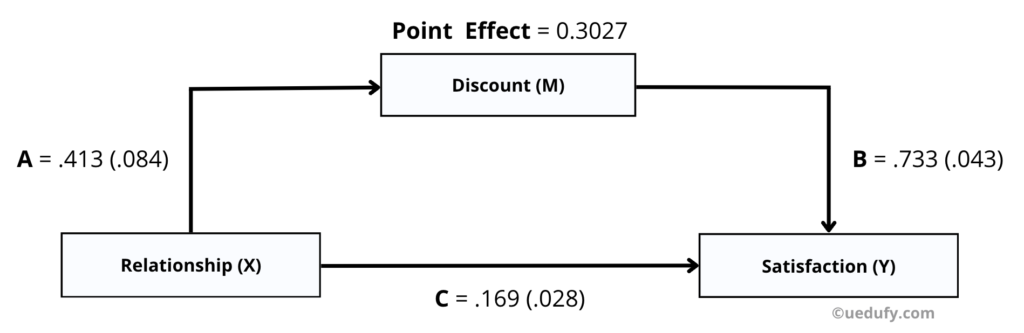
At this point, we got all the coefficients we need to estimate the indirect effect for the mediation analysis in our example. Let’s quickly recap the regression coefficients we have recorded so far:
Path A = .413 (.084)
Path B = .733 (.043)
Path C = .169 (.028)
- Test indirect effect for statistical significance.
To test whether our example’s indirect effect is statistically significant, we can use either bootstrapping or a Sobel Test.
In this method, we will use the Sobel Test as PROCESS macro uses bootstrapping in SPSS, and we will cover that in Method 2 of this lesson.
Sobel Test (Sobel, 1982) is a method used to estimate the statistical significance of indirect effect in mediation analysis. The Sobel Test is not available in SPSS. However, it can be done easily with any Sobel Test calculator online, such as the one available HERE.
Simply add the Unstandardized Coefficient Beta for A and B and the Std. Error coefficients for A and B in the Input fields sa and sb are seen in the image below.
Click the Calculate button. Sobel Test results will be displayed in the first row as highlighted in the following capture.
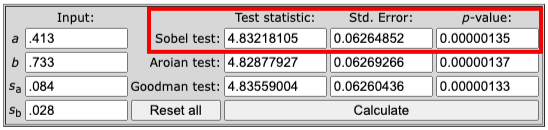
And the indirect effect analysis results for X → M → X using Sobel Test are as follows:
Test statistic = 4.83218105
Std. Error = 0.06264852
p-value = 0.00000135
The most important parameter here is the p-value which in this case is less than 0.05 therefore we can conclude that the indirect effect between relationship and satisfaction via discounts is statistically significant (p-value ≤ 0.05).
To find out the point estimate of the indirect effect at which the p-value in the Sobel Test is statistically significant, simply calculate the Unstandardized Coefficient Beta for A * B. For our example the calculation looks like this:
0.413 * 0.733 = 0.3027
0.3027 is the estimate of the indirect effect between relationship and satisfaction through discounts variables at the p-value of 0.00000135 as shown in the Sobel Test.
In a nutshell, this is how to run and interpret mediation analysis in SPSS. Next, let’s look at a second method to perform mediation analysis in SPSS.
Method 2: Mediation Analysis in SPSS using PROCESS
This method is more straightforward but requires installing the PROCESS macro extension in SPSS. The installation process is simple and won’t take more than 5 minutes.
- Launch PROCESS macro
Once installed, you can find the PROCESS macro in SPSS under Analyze → Regression → PROCESS v.x by Andrew F. Hayes.
- Add Satisfaction in the Y variable block, Relationship into the X variable block, and Discounts in the Mediator(s) block.
Select number 4 from the Model number drop-down menu.
By default, PROCESS macro does not accept more than 8 characters for your variable names. You can either rename your variables in SPSS to something shorter or check the option in the Long variable names in PROCESS.
- Click the Options button.
On the PROCESS options window, make sure the “Show total effect model (only models 4, 6, 80, 81, 82)” and “Standardized effects (mediation-only models)” checkboxes are selected.
Click Continue then OK to run mediation analysis in SPSS using PROCESS macro. This will take a few seconds due to the number of Bootstrap samples used by PROCESS.
That’s it. Your mediation analysis using PROCESS in SPSS is completed.
How to interpret Mediation Analysis in SPSS
This method provides us with pretty much the same mediation analysis details as the first method we discussed earlier but required much less effort on our behalf.
Let’s have a look at the mediation analysis results and learn which parameters are most relevant for interpretation of mediation results in your research paper.
The first section of mediation analysis results with PROCESS provides an overview of the mediation analysis, respectively, the X, Y, and M variables, the model used, and the sample size.
We can see the direct effect between the predictor variable Relationship (P-value = 0.000) and outcome variable Discounts is significant (P-value ≤ 0.05).
Next, we can observe the effect between predictors Relationship (P-value = 0.000) and Discounts (P-value = 0.000) on the outcome Satisfaction is significant (P-value ≤ 0.05).
Finally, let’s check the indirect effect of X on Y via mediator variable M with a point effect calculated at 0.3030.
In broad terms, this is how to interpret mediation analysis in SPSS using PROCESS macro.
We can see the mediation analysis results via Method 1 and 2 are similar. The only difference is the point effect for the indirect effect being rounded up from 0.3027 to 0.3030 in PROCESS macro.
Wrapping UP
In this lesson, we learned how to run mediation analysis in SPSS using two methods. Furthermore, we learned how to calculate the point effect and interpret mediation analysis in SPSS.
It is worth mentioning that other statistical techniques such as Structural Equation Modeling (SEM) also known as Path Analysis can be more efficient. However, SEM can be out of reach for many as it requires additional tools such as AMOS.
I recommend you go over the mediation analysis in SPSS a few times more to get familiar with the process before writing your mediation report in your research paper.
References
Sobel, M. E. (1982). Asymptotic intervals for indirect effects in structural equations models. In S. Leinhart (Ed.), Sociological methodology 1982 (pp.290-312). San Francisco: Jossey-Bass.

