In this article, we will explore the process of calculating the Pearson correlation coefficient in Excel using a practical example.
The Pearson correlation coefficient measures the linear relationship between two variables, and Excel provides a simple and efficient way to calculate it. Excel’s built-in functions make it easy to obtain the Pearson correlation coefficient with just a few clicks, whether you are working with a small or large data set.
If you don’t have yet a dataset at hand for this lesson, you can download mine below and follow along.
So, let’s buckle up and learn something new today!
What is Pearson correlation coefficient?
Let’s say you own a clothing store and want to see if there is a relationship between how much you spend on advertising and how much money you make. This is where the Pearson correlation coefficient comes in handy!
On the other hand, if the coefficient is close to -1, that means that as you spend more on advertising, your income is likely to decrease. And if the coefficient is close to 0, there’s no real relationship between advertising and revenue.
You looked at your data, and the Pearson correlation coefficient was 0.8. This means there’s a strong positive relationship between Advertising and Revenue – the more you spend on advertising, the more money you make! But don’t get too excited just yet. Other factors can affect income too. Knowing the Pearson correlation coefficient is just one piece of the puzzle – but an important metric to consider.
The Pearson correlation coefficient measures the strength of the relationship between two things, in this case, advertising and revenue. If the coefficient is close to 1, that means that as you spend more on advertising, you’ll likely see an increase in revenue.
r=\frac{\sum\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)}{\sqrt{\sum\left(x_i-\bar{x}\right)^2 \sum\left(y_i-\bar{y}\right)^2}}Where:
r = correlation coefficient
xi = values of the x-variable in a sample
x̄ = mean of the values of the x-variable
yi = values of the y-variable in a sample
ȳ = mean of the values of the y-variable
Assumptions
There are certain assumptions that must be met in order to use Pearson’s correlation coefficient accurately:
- Linearity: The relationship between the two variables should be linear, meaning that the change in one variable should be directly proportional to the change in the other variable.
- Independence: The observations should be independent, meaning that the value of one observation should not affect the value of another observation.
- Homoscedasticity: The variances of the two variables should be equal, meaning that the spread of the data around the mean should be similar for both variables.
- Normality: The data should be normally distributed, meaning that the distribution of the data should be roughly symmetrical and bell-shaped.
It is important to note that if these assumptions are not met, Pearson’s correlation coefficient may not accurately reflect the relationship between the two variables. In such cases, other methods of measuring the relationship, such as Spearman’s rank correlation coefficient, may be more appropriate.
Method 1: Calculate correlation coefficient in Excel using CORREL function
Let’s go back to our clothing store example and learn how to calculate Pearson correlation coefficient in Excel to find out if there is a relationship between how much we spend on advertising and how much money we make.
1. Prepare you data: Organize your data into two columns, with one column representing each of the two variables you want to analyze. In my dataset, the two variables we want to check if they are correlated are Advertising and Revenue.
2. Select a cell: Choose a cell in your worksheet where you would like to display the result of the Pearson correlation coefficient.

3. Enter the correlation function: Type “=CORREL(“ followed by the range of the first column of data, a semicolon, and the range of the second column of data, and close the parentheses. For example, if your data is in columns B and C (like in the capture below), the correlation function would look like this: =CORREL(B2:A13; C2:B13).
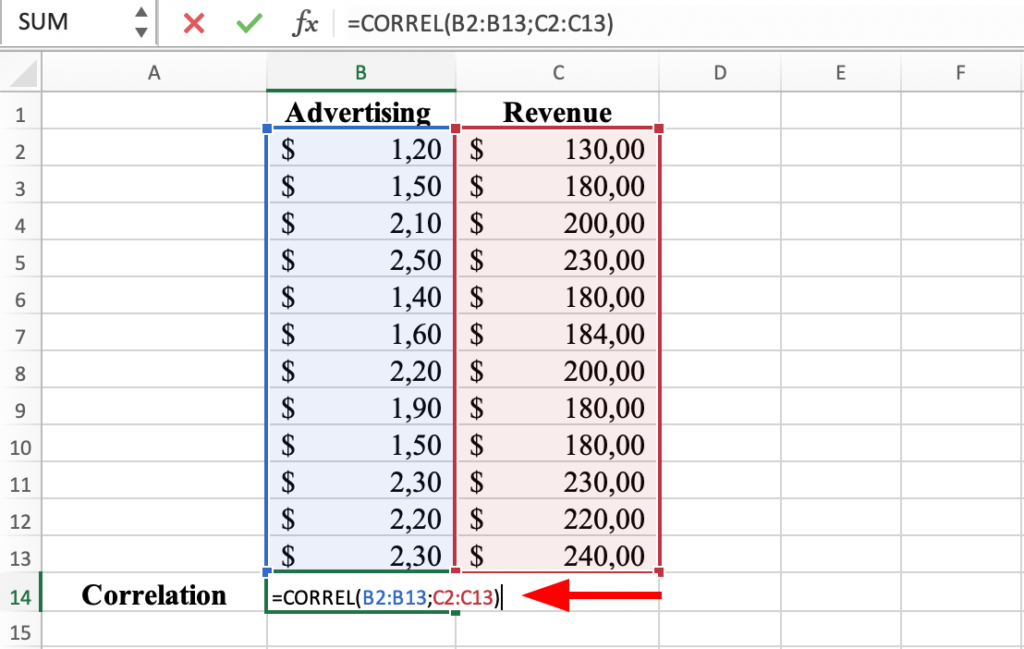
4. Calculate the result: Press the ENTER key to calculate the Pearson correlation coefficient. The result will be displayed in the selected cell. Hurrah! The correlation coefficient between Advertising and Revenue in our dataset is 0.9

Method 2: Calculate correlation coefficient using Analysis Tool in Excel
Here is another way to calculate the correlation between two variables in Excel, respectively using the Data Analysis Toolpak.
1. Prepare your data: Make sure your data is organized in two columns, each column representing a variable – same as we did before.
2. Install Data Analysis tool in Excel: if you don’t see the Data Analysis icon in your Data tab in Excel, you should head to the link above and follow the instructions to install it.

3. Launch the Data Analysis tool: From the Data tab, click on Data Analysis, and select Correlation.

4. Select the data: In the Data Analysis dialog box, select the input range, which is the range of the two columns of data. If you included the column labels in your selection (Advertising and Revenue), check the Labels in First Row checkbox.
NOTE: In the “Output Options” section, you can also choose where you want the result to be displayed, either in a new worksheet or in a range of cells. Let’s leave the default setting for now.

5. Run the analysis: Click on OK to compute. The result of the Pearson correlation coefficient will be displayed in the output location you selected. And is not a surprise that for the same data set, the coefficient is the same: 0.9.
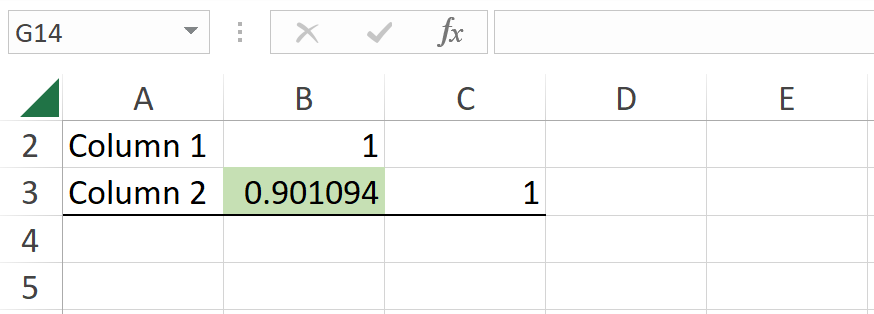
Interpret Pearson correlation coefficient result
The Pearson correlation coefficient will be a value between -1 and 1 where:
- A value of 1 indicates a perfect positive correlation
- A value of -1 indicates a perfect negative correlation
- A value of 0 indicates no correlation.
The closer the coefficient is to 1 or -1, the stronger the correlation between the two variables.
In our example, the correlation coefficient of 0.9 indicates a strong positive correlation between Advertising and Revenue variables.
NOTE: A correlation coefficient between 0.7 and 0.9 is considered a strong correlation, while a coefficient of 0.9 or higher is considered a very strong correlation.
In other words, if two variables have a Pearson correlation coefficient of 0.9, it means that as one variable increases, the other variable is likely to increase at a similar rate. This indicates a strong association between the two variables, but it does not prove causality.
It is important to note that a high Pearson correlation coefficient does not necessarily mean that one variable causes the other, only that there is a strong association between the two variables. Further analysis, such as regression analysis, may be needed to determine causality.
Conclusion
In conclusion, the Pearson correlation coefficient is a useful tool for understanding the relationship between two variables, and it is easy to calculate in Excel using either the “Data Analysis” tool or the CORREL function. I hope you found this article useful for your research and looking forward to seeing you soon.

