Welcome to this step-by-step guide on how to calculate Mean, Mode, and Median in Math! These concepts might seem intimidating initially, but they’re quite simple to understand – as you will see shortly. This article will break them down using real-life examples and easy-to-follow instructions.
If you’d like to learn more about mean, mode, and median, you can check our in-depth article on What is a measure of Central Tendency before getting down to calculus.
Lesson Outcomes
By the end of this lesson, you should be able to:
- Understand the concepts of mean, mode, and median in math
- Learn how to calculate mean, mode, and median using real-life examples
- Calculate mean, mode, and median in Excel
- Calculate mean, mode, and median in R
How To Calculate Mean in Statistics
The mean is what most people think of when they hear the word average. It’s the sum of all the values in a dataset divided by the total number of values.
To calculate the mean, follow these simple steps:
- Add up all the values in the dataset
- Divide the sum by the total number of values
Imagine you’re a teacher who wants to know the average test score of your class. The scores are as follows:
89, 76, 95, 82, 68, 91, 78
First, add up all the scores:
89 + 76 + 95 + 82 + 68 + 91 + 78 = 579
Next, divide the sum by the total number of scores (7):
579 / 7 = 82.7
So, the mean test score for your class is 82.7 points.
Calculate Mean in Excel
To calculate the mean in Excel, use the AVERAGE function. Follow these steps:
- Click on an empty cell where you want the mean to be displayed.
- Type
=AVERAGE(into the cell. - Select the range of cells containing the data you want to find the mean of, or manually type the cell range (e.g.,
A1:A10). - Close the parentheses and press Enter.
Example: =AVERAGE(A1:A10)
Calculate Mean in R
Calculating the mean in R is quite simple using the built-in mean() function. Here’s how to do it:
- Create a vector containing your dataset or use an existing one.
- Pass the vector to the
mean()function.
Here’s an example:
# Create a vector with sample data
data <- c(10, 20, 30, 40, 50)
# Calculate the mean
mean_value <- mean(data)
# Print the mean
print(mean_value)In this example, we created a vector named data containing five values (10, 20, 30, 40, 50). We then passed the data vector to the mean() function and stored the result in a variable named mean_value. Finally, we used the print() function to display the mean value of 30 in this case.
How To Calculate Mode in Statistics
The mode is the value that appears most frequently in a dataset. It’s the “crowd favorite” because it’s the value that occurs the most often. To find the mode, count the times each value appears in the dataset and identify the one that shows up the most.
Suppose you own a shoe store and want to know the most common shoe size among your customers. The shoe sizes of the last 20 customers are:
7, 8, 9, 7, 10, 9, 8, 7, 11, 10, 9, 7, 9, 8, 8, 10, 7, 9, 8, 10
To find the mode, count the frequency of each shoe size:
| Show sizes | Frequency |
| 7 | 5 times |
| 8 | 5 times |
| 9 | 6 times |
| 10 | 4 times |
| 11 | 1 time |
The Mode is size 9, appearing the most frequently (6 times).
Calculate Mode in Excel
To calculate the mode in Excel, you can use MODE.SNGL function for single-mode datasets or the MODE.MULT function for multimodal datasets. Here’s how to do it:
Single Mode:
A single-mode, unimodal dataset is a dataset with only one value appearing most frequently. In other words, there’s only one “peak” or “mode” in the data distribution.
- Click on an empty cell where you want the mode to be displayed.
- Type
=MODE.SNGL(into the cell. - Select the range of cells containing the data you want to find the mode of, or manually type the cell range (e.g.,
A1:A10). - Close the parentheses and press Enter.
Example:
=MODE.SNGL(A1:A10)Multiple Mode:
A multi-mode dataset, or multimodal, refers to a dataset with more than one value appearing most frequently. In other words, there are multiple “peaks” or “modes” in the data distribution.
- Click on an empty cell where you want the first mode to be displayed.
- Type
=MODE.MULT(into the cell. - Select the range of cells containing the data you want to find the modes of, or manually type the cell range (e.g.,
A1:A10). - Close the parentheses and press Enter.
- To display additional modes, copy the formula into adjacent cells.
Example:
=MODE.MULT(A1:A10)Using these Excel functions lets you quickly and easily calculate the Mode(s) for any dataset in your spreadsheet.
How To Calculate Median In Statistics
The median is the middle value in a dataset when the values are arranged in ascending or descending order. It represents the midpoint, where half of the values are above it and half are below it. To find the median, follow these steps:
- Arrange the values in ascending order
- Identify the middle value
If there’s an odd number of values, the median is the exact middle value. If there’s an even number of values, the median is the mean of the two middle values.
Imagine you’re a researcher analyzing the income of 9 households in a neighborhood. The incomes are (in thousands of dollars):
45, 60, 70, 55, 80, 90, 65, 75, 50
First, arrange the incomes in ascending order:
45, 50, 55, 60, 65, 70, 75, 80, 90
Since there are 9 households (an odd number), the median is the exact middle value:
Median Income = 65
So, the median income in this neighbourhood is $65,000.
Calculate Median in Excel
To calculate the median in Excel, you can use the MEDIAN function. Here’s how to do it:
- Click on an empty cell where you want the median to be displayed.
- Type
=MEDIAN(into the cell. - Select the range of cells containing the data you want to find the median of, or manually type the cell range (e.g.,
A1:A10). - Close the parentheses and press Enter.
Example:
=MEDIAN(A1:A10)Calculate Median in R
To calculate the median of a dataset in R, you can use the built-in median() function. Here’s a step-by-step guide on how to do this:
- First, could you create a vector that contains your data? For example, you can create a vector called
data:
data <- c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10)
- Now, use the
median()function to calculate the median of the dataset:
data_median <- median(data)
- Finally, you can print the median value:
print(data_median)Putting it all together, your R script would look like this:
data <- c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10)
data_median <- median(data)
print(data_median)When you run this R script, it will output the median value of the dataset, which is 5.5 in this case.
How To Calculate Mean, Mode, and Median in R in One Go
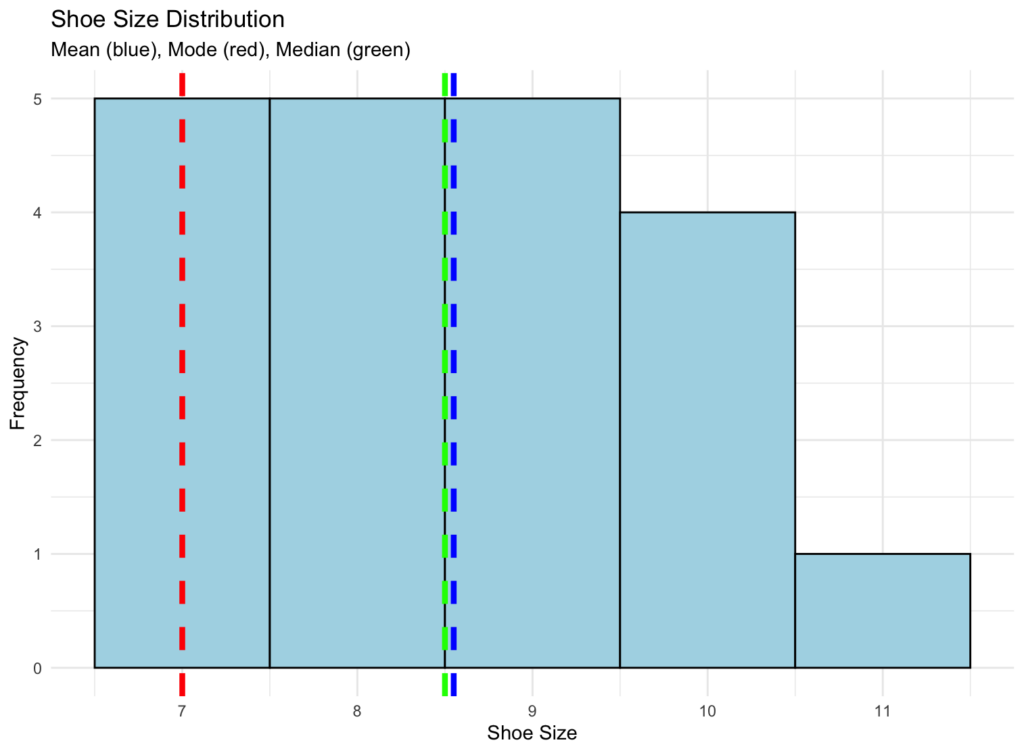
Let’s use our shoe size example from earlier. Here’s the R code to generate a histogram and display the mean, mode, and median on the plot:
# Load required libraries
library(ggplot2)
# Dataset
shoe_sizes <- c(7, 8, 9, 7, 10, 9, 8, 7, 11, 10, 9, 7, 9, 8, 8, 10, 7, 9, 8, 10)
# Calculate mean, mode, and median
mean_size <- mean(shoe_sizes)
mode_size <- as.numeric(names(which.max(table(shoe_sizes))))
median_size <- median(shoe_sizes)
# Create the histogram
hist_plot <- ggplot(data.frame(shoe_sizes), aes(shoe_sizes)) +
geom_histogram(binwidth = 1, fill = "lightblue", color = "black") +
geom_vline(aes(xintercept = mean_size), color = "blue", linetype = "dashed", size = 1.5) +
geom_vline(aes(xintercept = mode_size), color = "red", linetype = "dashed", size = 1.5) +
geom_vline(aes(xintercept = median_size), color = "green", linetype = "dashed", size = 1.5) +
labs(title = "Shoe Size Distribution",
subtitle = "Mean (blue), Mode (red), Median (green)",
x = "Shoe Size",
y = "Frequency") +
theme_minimal()
# Display the plot
print(hist_plot)This code will generate a histogram of the shoe size data with vertical dashed lines representing the mean (blue), mode (red), and median (green), as seen below. It’s a great way to visualize the data and understand the relationship between these three measures of central tendency.
Wrapping Up
In a nutshell, this article breaks down key basics like mean, mode, and median in statistics. We also learned how to calculate the measures of central tendency by hand, in Excel and R. We hope we kept it light and easy so you can grasp these concepts without breaking a sweat.
As you explore the world of statistics, please remember to revisit the Pre-Statistics section to make sure you understand. Happy number-crunching!

