Hey there! If you’ve ever wondered what is a measure of central tendency, then you’re in the right place. We’re going to break down this somewhat intimidating term into simple, easy-to-understand pieces.
Lesson Outcomes
By the end of this article, you should be able to:
- Understand the concept of measures of central tendency and their importance in statistics and data analysis.
- Define and differentiate between mean, median, and mode as measures of central tendency.
- Explain the formulas and procedures to calculate the mean, median, and mode.
- Recognize the differences in sensitivity to outliers and applicability among mean, median, and mode.
- Interpret histograms and identify the positions of mean, median, and mode in the data distribution.
So, let’s dive in!
So, What is a Measure of Central Tendency Anyway?
In a nutshell, a measure of central tendency is a single value that represents the center or the typical value of a dataset. It’s a way to summarize a whole bunch of data points with just one number. Measures of central tendency help us understand the general behavior or trend of a dataset, making it easier to draw conclusions and make decisions based on the data.
There are three main measures of central tendency: the mean, the median, and the mode. Let’s explore each of these in more detail.
1. Mean: The Average Joe of Central Tendency
The mean often called the average, is the most common measure of central tendency. It’s calculated by adding all the data points in a dataset and dividing them by the total number of data points. Here’s the mean formula:
\begin{equation}
\bar{x} = \frac{1}{n} \sum_{i=1}^{n} x_i
\end{equation}
Where:
- x̄: This symbol represents the mean (average) of the dataset.
- n: This represents the total number of data points in the dataset.
- xᵢ: This represents each individual data point in the dataset, where i is the index ranging from 1 to n.
- Σ (from i=1 to n): This is the summation symbol, which indicates that we should sum the values of xᵢ for all indices from 1 to n. In other words, add up all the data points in the dataset.
When we are looking for a graphical representation of the mean, we should obtain something like the histogram bellow. Here, we generate a dataset of 100 random numbers with a mean of 50 and a standard deviation of 10.
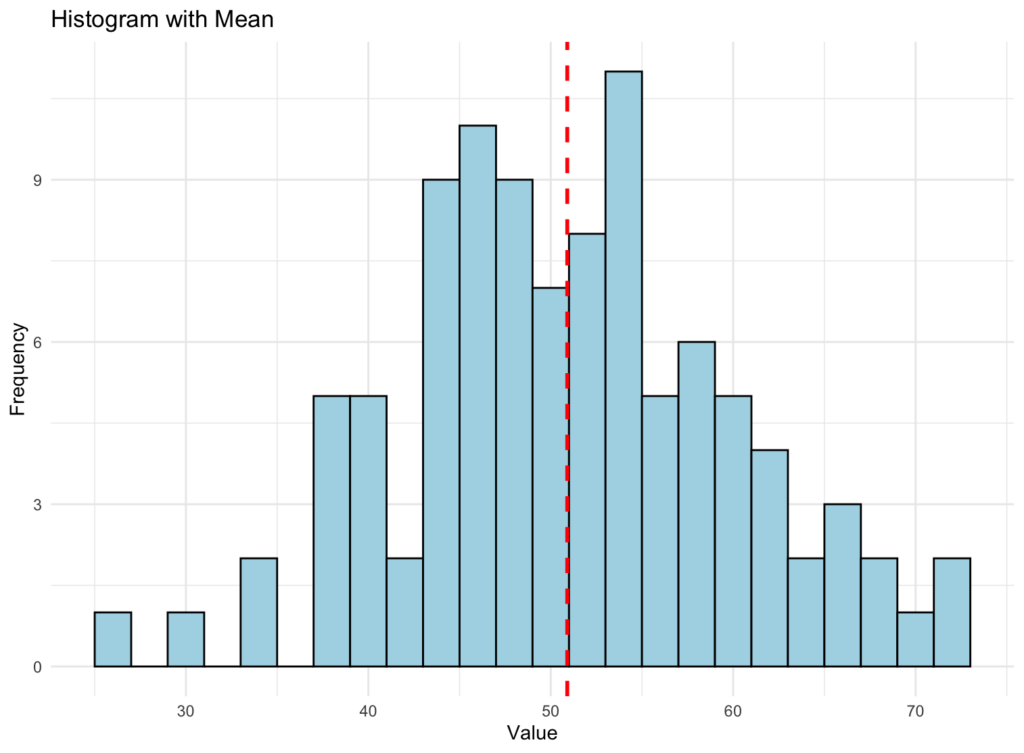
NOTE:
- A histogram is a visual representation of the dataset. It divides the data into a certain number of bins (groups), and the height of each bar in the histogram represents the frequency (how many times) the data points fall into that specific bin. In other words, taller bars indicate more data points in that range of values.
- The vertical red-dotted line in the graphic above represents the mean value of the dataset. The mean is calculated by adding all the data points and dividing the sum by the total number of data points. It provides an idea of the central tendency or “average” of the data.
When you look at the graphic, you can see how the data is distributed, and the vertical line helps you identify where the mean value lies within that distribution. This can give you a general sense of the overall trend in the data and help you understand the dataset’s behavior better.
However, it’s important to remember that the mean can be sensitive to outliers (extreme values), which might skew the mean and make it less representative of the dataset’s central tendency.
Learn how to calculate Mean by hand, Excel, and R in just a few simple steps.
2. Median: The Middle Child of Central Tendency
The median is the middle value in a dataset when the data points are arranged in ascending or descending order. It’s like the middle child of central tendency – often overlooked but still super important.
To find the median, first sort the dataset in ascending or descending order. If there’s an odd number of data points, the median is the middle value. If there’s an even number of data points, the median is the average of the two middle values. Here’s a quick example:
- Dataset: $2, 4, 6, 8, 10$. The median is 6 because it’s the middle value.
- Dataset: $2, 4, 6, 8$. The median is 5 because the average is 4 and 6, the two middle values.
One great thing about the median is that it’s less sensitive to extreme values, which means it can better represent the center for skewed distributions.
Here is how the graphical representation of a median looks like using the same data-set criteria we used earlier:
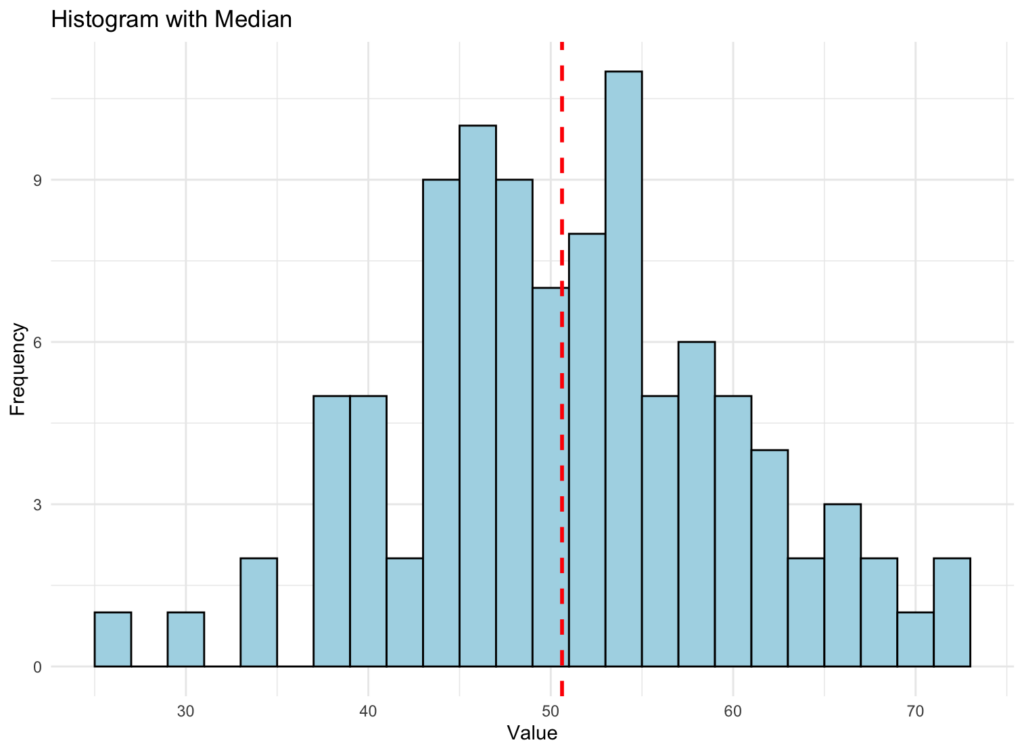
The median histogram above may look similar to the previous one we generated for the mean. Still, if you pay attention, the red-dotted line representing the median is slightly off. Here is the explanation why:
- The mean (average) is calculated by adding up all the data points and dividing the sum by the total number of data points. It gives an idea of the central tendency or “average” of the data. However, the mean can be sensitive to outliers (extreme values) and may not represent the true center of the dataset when outliers are present.
- The median is the middle value of the dataset represented. by the red-dotted line when the data is sorted in ascending or descending order. If there is an even number of data points, the median is the average of the two middle values. The median is less sensitive to outliers than the mean and can better represent the dataset’s central tendency when outliers are present.
NOTE: In the generated histograms, the vertical lines for the mean and median are slightly different because they represent different measures of central tendency. Their positions may vary depending on the dataset’s distribution of data points. In some cases, the mean and median may be close or equal. In contrast, in other cases, they may be different due to the presence of outliers or the specific distribution of the data.
Learn how to calculate the median by hand, Excel, and R easily.
3. Mode: The Most Popular Kid on the Block
The mode is the value that occurs most frequently in a dataset. It’s like the most popular kid in school – everyone wants to hang out with them.
Unlike the mean, there isn’t a specific mathematical equation to calculate the mode. The mode is simply the value or values that occur most frequently in a dataset. To find the mode, you need to count the frequency of each unique value in the dataset and identify the one(s) with the highest frequency.
In some cases, a dataset might have:
- One mode (unimodal): A single value occurs more frequently than any other value.
- Two modes (bimodal): Two different values occur with the same highest frequency.
- Multiple modes (multimodal): More than two values occur with the same highest frequency.
- No mode: All values in the dataset occur with the same frequency.
It’s important to note that the mode can be used for any type of data, including nominal, ordinal, interval, or ratio data, as it only relies on the frequency of each unique value.
The histogram for the mode, along with a vertical line representing the mode value, looks like this:
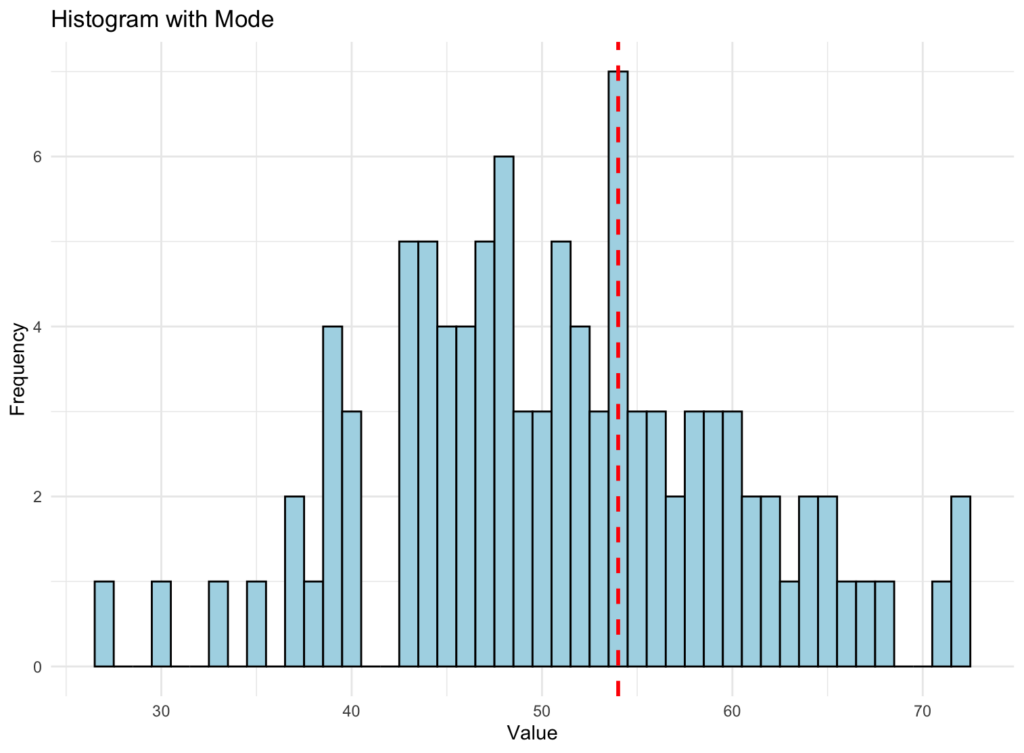
Here’s a simple breakdown of what the mode histogram above tells us:
- The histogram is a visual representation of the dataset. It divides the data into a certain number of bins (groups), and the height of each bar in the histogram represents the frequency (how many times) the data points fall into that specific bin. In other words, taller bars indicate more data points in that range of values.
- The vertical red-dotted line in the graphic represents the mode value of the dataset. The mode is the value that occurs most frequently in the dataset. It is a measure of central tendency that can help identify the dataset’s most common value or values.
When looking at the mode histogram, you can see how the data is distributed, and the vertical line helps you identify where the mode value(s) lie within that distribution.
The mode can provide insights into the dataset’s general behavior and help you understand the most common values. Unlike the mean and median, the mode is unaffected by outliers or extreme values, making it a suitable measure of central tendency when the dataset has a skewed distribution or contains outliers.
Learn how to calculate mode by hand, Excel, and R quickly.
Why Do We Care About Measures of Central Tendency?
Measures of central tendency are used to analyze and interpret data in various fields, such as statistics, economics, psychology, and other sciences. They help us to:
- Summarize large datasets: Instead of analyzing every single data point, we can use a measure of central tendency to get a general idea of what the data looks like. This simplifies our analysis and makes understanding the overall pattern or trend in the data easier.
- Compare different datasets: Measures of central tendency allow us to compare datasets by providing a single value representing each dataset’s center. This makes it easier to see which dataset has higher or lower values on average.
- Identify trends and patterns: By looking at the mean, median, or mode, we can identify trends and patterns in the data. This can be useful for making predictions, identifying areas for improvement, or monitoring changes over time.
- Make informed decisions: In many fields, decision-makers rely on measures of central tendency to guide their choices. For example, a business owner might look at the average revenue of different products to decide which ones to focus on promoting, or a teacher might use the median test score to determine the effectiveness of their teaching methods.
How To Choose The Right Measure of Central Tendency
Now that you know what a measure of central tendency is and why it’s important, you might be wondering which one to use in different situations. Here are some general guidelines to help you choose the right measure for your needs:
- Use the mean when: Your data is relatively symmetric and free of extreme values or outliers. The mean is great for providing an overall trend in the data and is commonly used in many fields.
- Use the median when: Your data is skewed or has extreme values that might affect the mean. The median is less sensitive to outliers and better represents the center for skewed distributions.
- Use the mode when: You want to identify a dataset’s most frequent or popular value. The mode is particularly useful for categorical or discrete data where other measures of central tendency might not be applicable.
Wrapping Up
So, there you have it! You now know the answer to the question, “What is a measure of central tendency?” and why it’s important. Measures of central tendency, such as the mean, median, and mode, help us summarize and understand data, making it easier to draw conclusions and make decisions based on the data.
By choosing the right measure of central tendency for your specific situation, you’ll be well on your way to becoming a statistics superstar.

