What is linearity in statistics, you may ask? Well, have you ever looked at a scatter plot and noticed a pattern that seems to form a straight line? That’s when linearity in statistics comes into play. In this article, we’ll dive into the world of linearity, explore what it means, and discuss its importance in various statistical methods.
So, buckle up, and let’s hit the road!
The Basics: What is Linearity in Statistics?
Linearity in statistics is all about relationships. But not just any relationships – we’re talking about those where a change in one variable directly corresponds to a change in another variable. Imagine a straight line connecting two points on a graph; that’s a linear relationship in action: the straighter the line, the more “linear” the relationship between the variables.
A simple example of a linear relationship is the connection between the distance you travel and the time it takes to get there. If you travel at a constant speed, the relationship between distance and time will be linear, meaning that if you double the time, you’ll also double the distance.
Equations Galore!
When dealing with linearity in statistics, we often represent the relationship between variables using a linear equation. In the simplest case, involving two variables (x and y), the linear relationship can be represented by the equation:
y = mx + b
Here, m represents the slope (rate of change) of the line, b is the y-intercept (the value of y when x = 0), and x and y are the independent and dependent variables, respectively. You can think of the slope as the “steepness” of the line, while the y-intercept is where the line crosses the y-axis.
Let’s dive into an example. Suppose you want to predict the price of a pizza based on its size (in inches). You gather some data and discover that the relationship between size (x) and price (y) is linear, with a slope (m) of 2 and a y-intercept (b) of 5. Your linear equation would look like this:
y = 2x + 5
Now, if you want to find out the price of a 12-inch pizza, plug in the value for x:
y = 2(12) + 5 = 24 + 5 = 29
So, a 12-inch pizza would cost $29. You be the judge if that is too much or too little 😛
Why Should We Care About Linearity?
Well, linearity is the backbone of many statistical techniques that help us understand trends, patterns, and relationships between variables. It’s vital in fields like social sciences, economics, and natural sciences. Let’s dive into some of the reasons why linearity is so important:
1. Regression Analysis
One of the most common uses of linearity is in regression analysis. Regression analysis is about finding a mathematical model that best fits a set of data points. When there’s a linear relationship between variables, we can use a technique called linear regression to find the best-fitting line.
If we assume that there’s a straight-up relationship between the variables, but there isn’t, we might not get accurate results. We might end up with a model that doesn’t describe the behaviour of the variables we’re interested in, or we might make predictions that are way off.
For example, let’s say we’re trying to figure out how temperature affects the growth of plants. We assume that there’s a straight-up relationship between temperature and growth, so we use linear regression to make predictions. But if the relationship between temperature and growth isn’t straight-up (maybe there’s a sweet spot where growth is highest, but it’s not a straight line), then our linear regression model might not be accurate. We might make predictions that don’t reflect what would happen in the real world.
That’s why it’s important to test for linearity before we start doing linear regression. We need to make sure that the relationship between the variables is linear before we assume that it is. If there isn’t a straight-up relationship, we might need to transform the data or use a different model to capture the behavior of the variables accurately.
By testing for linearity in regression, we can be confident that our linear regression results accurately reflect the relationship between the variables we’re interested in.
2. Correlation
Another reason to care about linearity is that it’s crucial for understanding correlation. Correlation is a measure of how strongly two variables are related. When the relationship between variables is linear, the correlation coefficient (usually represented by “r” or “rho”) can give us valuable insights into the strength and direction of the relationship.
A correlation coefficient of +1 indicates a perfect positive linear relationship, while a correlation coefficient of -1 signifies a perfect negative linear relationship. A 0 would mean – as you might guess – no linear relationship.
For instance, let’s say you want to know if there’s a relationship between the number of hours students study and their exam scores. By calculating the correlation coefficient, you can determine the strength and direction of the linear relationship between these two variables.
3. Analysis of Variance (ANOVA)
When we do statistics stuff like ANOVA (which compares the means of two or more groups), we gotta make sure there’s a straight-up relationship between the variables we’re looking at. That’s what we call linearity. We need to make sure that the effect of the independent variable(s) on the dependent variable is the same across all levels of the independent variable(s).
If we don’t check for linearity, we might end up with some messed-up results. For example, let’s say we’re comparing the test scores of three groups (A, B, and C). If there’s a straight-up connection between the group and test scores, we can use ANOVA to see if there are any differences in the mean scores between the three groups.
But if the relationship between the group and test scores isn’t straight-up (maybe it’s curved or something), then ANOVA might not be accurate. If the effect of the group on test scores changes depending on the level of the group, then using ANOVA to test for group differences might lead to incorrect conclusions.
That’s why it’s important to test for linearity in ANOVA and make sure there’s a straight-up relationship between the variables we’re looking at. If there isn’t, we might need to transform the data or use a different model. By making sure there’s linearity, we can be confident that our ANOVA results accurately reflect the differences between groups and let us draw real conclusions about the populations we’re studying.
4. Hypothesis Testing
So, in statistics, hypothesis testing is a way to figure out if two things are related to each other or not. We usually start by assuming that there’s no relationship between the things we’re looking at (this is called the null hypothesis). Then, we collect data and do some calculations to figure out if there’s enough evidence to reject the null hypothesis and conclude that there is a relationship between the variables.
But here’s the thing: if we assume there’s a straight-up relationship between the variables, but there isn’t, we might end up rejecting the null hypothesis when we shouldn’t. That’s where linearity comes in. We need to make sure that there’s actually a straight-up relationship between the variables we’re testing before we start doing hypothesis testing.
For example, let’s say we’re testing whether there’s a relationship between the number of hours someone exercises per week and their cholesterol levels. If there’s a straight-up relationship between these things, we can use hypothesis testing to see if there’s enough evidence to conclude that exercising more leads to lower cholesterol levels.
But if the relationship between exercise and cholesterol isn’t straight-up (maybe it’s curved or something), then our hypothesis testing might not be accurate. We might end up rejecting the null hypothesis and concluding that there is a relationship between the variables when there isn’t.
5. Design of Experiments
In statistics, the design of experiments is a way to figure out how different variables affect an outcome. For example, if we’re trying to figure out what factors affect plant growth, we might manipulate things like light, water, and fertilizer to see how they affect the plants.
But here’s the thing: we assume that the effect of each variable on the outcome is linear. That’s where linearity comes in. We need to make sure that the relationship between the variables and the outcome is linear before we start designing our experiment.
If we assume that there’s a straight-up relationship between a variable and the outcome, but there isn’t, we might not get the results we’re looking for. We might manipulate the variable and not see any effect on the outcome, or we might see an effect that’s different from what we expected.
For example, let’s say we’re trying to figure out how different levels of light affect plant growth. We assume that there’s a straight-up relationship between light and growth, so we design our experiment to test different levels of light. But if the relationship between light and growth isn’t straight-up (maybe growth levels off after a certain point), then our experiment might not be accurate. We might manipulate the light and not see any effect on growth, or we might see a different effect than we expected.
So, it should be pretty clear why testing for linearity before we start designing our experiment is crucial. We need to make sure that the effect of each variable on the outcome is linear before we assume that it is – right? If there isn’t a straight-up relationship, we might need to use a different experimental design or model to capture the behavior of the variables accurately.
So, What Happens When We Mess Up Linearity?
It’s super important to make sure we have a linear relationship before we use a linear regression model. If we don’t, our predictions will be off, and we might not get the results we’re looking for. It could even make us think there’s a connection where there isn’t one. That’s why we need to check for linearity before we start making predictions.
If we violate the linearity assumption, we can get all sorts of messed-up results. For example, if we’re trying to predict house prices based on square footage, we might think we can use a linear model. But if the relationship between house prices and square footage isn’t linear (maybe the prices go up in a weird way as square footage increases), then our linear regression model won’t work.
That’s why it’s key to always test for linearity before we use a linear regression model. If we don’t, we might end up with bad predictions, bad estimates of coefficients, or just bad results overall. By taking the time to check for linearity, we can make sure our models accurately reflect the real world and give us useful insights into the things we’re interested in.
How to Determine Linearity in Statistics?
By now, we know that linearity in statistics is important, but how do we actually test for it? There are a few ways we can do so:
- Scatterplots: A scatterplot is a graph that shows how two things are related to each other. If there’s a linear relationship, the points on the scatterplot will form a straight line.
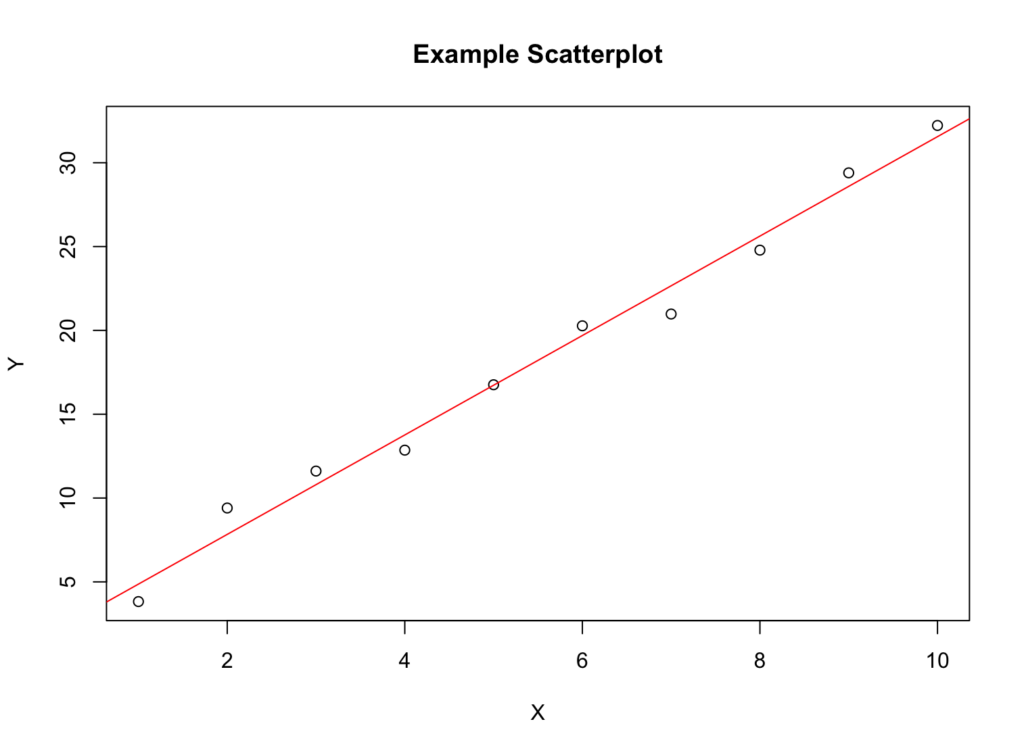
- Correlation coefficient: The correlation coefficient measures the strength of the relationship between two things. If there’s a linear relationship, the correlation coefficient will be close to 1 (or -1 if it’s a negative relationship). For example, the correlation coefficient of 0.9975461 indicates a strong positive linear relationship between variables.
- Residual plots: A residual plot shows how far off our predictions are from the actual values. If there’s a pattern in the residual plot, our linear model might not be accurate.
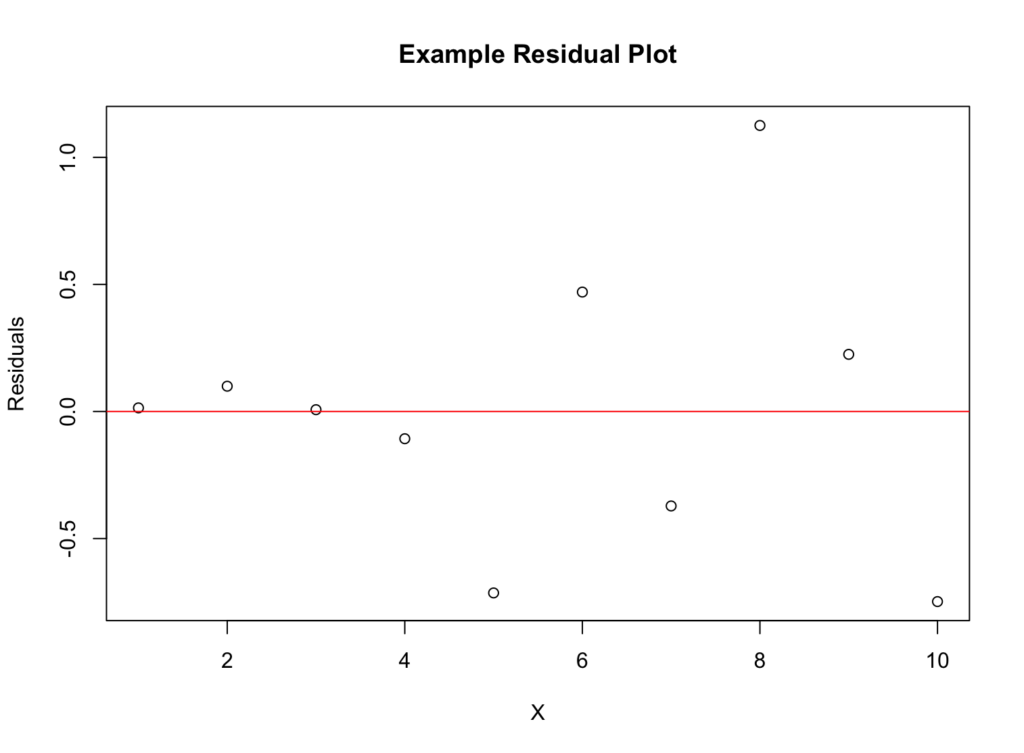
By using these statistical tests, we can figure out if there’s a linear relationship between two variables or not. If there is, we can use a linear regression model to make predictions. If there isn’t, we’ll need to use a different model or transform our data to make the relationship linear.
Conclusion
So, in a nutshell, linearity is a big deal in statistics. Whether you’re crunching numbers with linear regression, comparing means with ANOVA, or testing hypotheses, you’ve got to make sure there’s a straight-up relationship between the variables you’re looking at.
By testing for linearity, you can avoid bogus results and make sure your conclusions are on point. So next time you’re running some stats, remember to keep linearity in mind, and you’ll be all set 👍

