Hey there! If you’re new to the world of statistics and research, you might’ve come across the term homoscedasticity assumption and wondered what on earth it means.
Fear not! We’re here to break it down for you in a friendly, informal manner, with some relatable examples. So, grab a cup of tea, sit back, and let’s dive into the fascinating world of homoscedasticity vs. heteroscedasticity.
What is Homoscedasticity Assumption?
Homoscedasticity (pronounced “homo-sked-asticity”) is a fancy term in statistics that describes the consistency of variance in a dataset. In simpler terms, it means that the spread or dispersion of your data points remains constant across different levels of an independent variable. If you’re still scratching your head, don’t worry! We’ll use some examples to make it crystal clear.
Picture yourself in a classroom setting. The teacher decides to give a pop quiz to test the students’ knowledge of a particular subject. If the quiz is designed fairly, the scores should be evenly spread across all students, regardless of their abilities. This is an example of homoscedasticity. In this case, the variance in scores doesn’t change with the level of student ability.
Heteroscedasticity (the opposite of homoscedasticity) occurs when the spread or dispersion of data points is not consistent across different levels of an independent variable. In our classroom example, this would mean that the variance in scores changes with the student’s ability level – perhaps the quiz is too difficult for some students and too easy for others.
Homoscedasticity and Linear Regression
Homoscedasticity is an important assumption in linear regression for several reasons. It helps to ensure the validity, reliability, and interpretability of the results. Let’s discuss some specific reasons why homoscedasticity is important in linear regression:
- Efficiency of estimators: In linear regression, the goal is to estimate the coefficients (i.e., the slope and the intercept) that best describe the relationship between the dependent and independent variables. When the homoscedasticity assumption holds, the ordinary least squares (OLS) method used to estimate these coefficients is known to be the best linear unbiased estimator (BLUE). This means that among all linear unbiased estimators, OLS provides the smallest variance. If the data is heteroscedastic, the OLS estimators may still be unbiased, but they are no longer efficient, which means there may be other estimators with smaller variances.
- Validity of hypothesis tests: Linear regression often involves hypothesis testing to determine the significance of the estimated coefficients. These tests, like the t-test and F-test, are based on the assumption of homoscedasticity. If this assumption is violated, the test statistics and p-values may be unreliable, leading to incorrect conclusions about the significance of the coefficients.
- Confidence intervals: Confidence intervals for the estimated coefficients are also affected by the homoscedasticity assumption. If the data is homoscedastic, the confidence intervals will be accurate and provide a reliable measure of the uncertainty around the estimates. However, if the data is heteroscedastic, the confidence intervals may be too wide or too narrow, leading to incorrect inferences about the true population parameters.
- Predictive accuracy: Homoscedasticity is important for making accurate predictions using the regression model. If the data is homoscedastic, the model’s residuals (i.e., the differences between the observed and predicted values) will have a constant variance across all levels of the independent variable. This means that the model’s predictive accuracy is consistent across the entire range of the independent variable. In contrast, if the data is heteroscedastic, the model’s predictive accuracy may be compromised, as the residuals may exhibit varying levels of variability across the range of the independent variable.
Recognizing Homoscedasticity (and Heteroscedasticity)
Now that we’ve covered what homoscedasticity is and why it’s important let’s discuss how to recognize it in your data. There are a few different ways to check for homoscedasticity, including graphical methods and statistical tests.
Graphical Methods
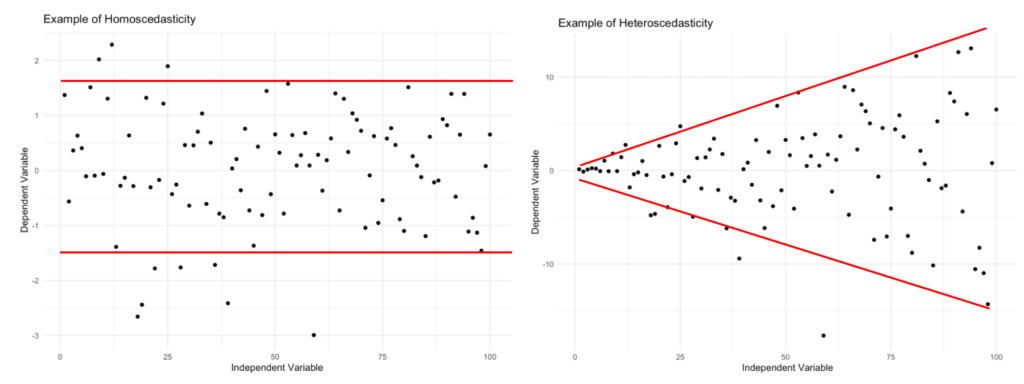
One of the simplest ways to check for homoscedasticity is by creating a scatterplot of your data. If the data is homoscedastic, the points should be evenly dispersed across the entire range of the independent variable. In other words, there shouldn’t be any noticeable patterns or clusters in the data points.
Statistical Tests
If you prefer a more formal approach, there are several statistical tests available to check for homoscedasticity. Some popular tests include:
- Bartlett’s Test: This test checks for equal variances in multiple groups by comparing the variances of each group. If the test statistic is significant, it indicates that the data is heteroscedastic, and the assumption of homoscedasticity is violated.
- Levene’s Test: Similar to Bartlett’s Test, Levene’s Test also checks for equal variances across multiple groups. However, Levene’s Test is less sensitive to non-normality, making it a more robust option in cases where the data may not be normally distributed.
- Breusch-Pagan Test: This test is used specifically in the context of regression analysis. It tests for heteroscedasticity by checking whether the squared residuals from a regression model are related to one or more independent variables. If the test is significant, it indicates that heteroscedasticity is present.
- White Test: Another test used in regression analysis, the White Test, is a more general test for heteroscedasticity. It examines whether the squared residuals from a regression model are related to any linear or quadratic combinations of the independent variables. If the test is significant, it suggests the presence of heteroscedasticity.
Here is a quick example of how to test homoscedasticity in R including both graphical and statistical methods (Breusch-Pagan test).
Keep in mind that no single test is perfect, and each has its limitations. In some cases, it might be helpful to use multiple tests or combine them with graphical methods to get a more accurate assessment of homoscedasticity.
Addressing Heteroscedasticity
If you find that your data is heteroscedastic, don’t panic! There are several strategies you can use to address this issue and improve the quality of your analysis:
- Transformation: Sometimes, transforming one or more variables in your dataset can help to stabilize the variance and achieve homoscedasticity. Common transformations include taking the logarithm, square root, or reciprocal of a variable. Be cautious, though, as transforming your data can also change the interpretation of your results.
- Weighted Regression: In the context of regression analysis, you can use weighted regression techniques to give more weight to observations with smaller variances and less weight to those with larger variances. This helps to stabilize the variance across the range of the independent variable and can improve the accuracy of your model.
- Robust Regression: Another option for addressing heteroscedasticity in regression analysis is to use robust regression techniques. These methods are designed to be less sensitive to outliers and violations of assumptions (like homoscedasticity) and can provide more accurate estimates when the data is heteroscedastic.
- Bootstrapping: Bootstrapping is a resampling technique that can help to overcome some of the issues associated with heteroscedasticity. By repeatedly resampling your data and calculating the statistic of interest, you can obtain a more accurate estimate of the true population parameter, even when the data is heteroscedastic.
Homoscedasticity vs. Heteroscedasticity: Key Differences
So, by now you should already have a fair understanding of the key differences between homoscedasticity and heteroscedasticity and their importance in statistics. If still in the shadow, let me enumerate them for you as follows:
- Consistency of variance: Homoscedasticity refers to a situation where the variance (i.e., the spread or dispersion) of data points remains constant across different levels of an independent variable. In other words, the variability in the dependent variable does not change as the independent variable changes. Heteroscedasticity, on the other hand, occurs when the variance of the data points is not consistent across different levels of the independent variable. In this case, the variability in the dependent variable changes as the independent variable changes.
- Data distribution: In a homoscedastic dataset, the data points are evenly dispersed across the entire range of the independent variable, and there shouldn’t be any noticeable patterns or clusters. In a heteroscedastic dataset, you may observe patterns in the data points, such as a funnel shape or a fan shape, where the dispersion of data points increases or decreases as the independent variable changes.
- Assumptions of statistical tests: Many statistical tests and models, such as linear regression, t-tests, and analysis of variance (ANOVA), rely on the assumption of homoscedasticity. If this assumption is violated (i.e., the data is heteroscedastic), the results of these tests may be inaccurate or misleading. In such cases, researchers may need to use alternative methods, such as weighted regression, robust regression, or data transformation, to address the issue of heteroscedasticity.
- Impact on statistical analysis: Homoscedasticity is generally considered desirable in statistical analysis because it helps to ensure the validity and reliability of your results. When your data is homoscedastic, you can be more confident that your conclusions are trustworthy and that your predictions will be more accurate. On the other hand, heteroscedasticity can lead to biased or inefficient estimates, affecting the accuracy and reliability of your analysis.
To summarise, the key differences between homoscedasticity and heteroscedasticity lie in the consistency of variance across different levels of the independent variable, the distribution of data points, the assumptions of statistical tests, and the impact on the validity and reliability of statistical analysis.
Wrapping Up
In conclusion, homoscedasticity is an important concept in statistics and research that helps ensure the validity and reliability of your results. By understanding what homoscedasticity is, why it matters, and how to recognize and address it in your data, you’ll be well on your way to conducting high-quality research and making meaningful conclusions.
Just remember that no single technique is perfect, and it’s essential to use your judgment and knowledge of the specific research context to make the best decisions for your analysis. Happy researching!

