How To Test Homoscedasticity in R: 2 Easy Methods

Hey there, data enthusiasts! Today, we will learn how to test homoscedasticity in R using 2 easy to follow methods: a visual method and a statistical test.

The visual method involves plotting the residuals against the fitted values, while the statistical test we’ll be using is the Breusch-Pagan test. Both methods are commonly used to check for homoscedasticity in linear regression models.

If you still wonder, “What on earth is homoscedasticity, and why should I care?” Well, homoscedasticity is a key assumption in linear regression, and it refers to the constant variance of errors or residuals across the range of predictor variables. It might initially sound intimidating, but trust us, it’s much easier than you think!

So, let’s get started on our journey to explore testing for homoscedasticity in R using the ever-popular mtcars dataset. Alternatively, you can use your own dataset and follow along.

Test Homoscedasticity in R using the Visual Method

First, let’s take a moment to understand the dataset we’ll work with mtcars. The mtcars dataset is in-built in R, containing information on 32 cars from a 1974 Motor Trend magazine issue. It includes 11 variables, such as miles per gallon (mpg), cylinders (cyl), horsepower (hp), and others. This dataset is widely used for teaching and learning purposes, making it a perfect choice for our tutorial.

Let’s start by creating a simple linear regression model using the mtcars dataset. We’ll use the ‘mpg‘ (miles per gallon) variable as the response and the ‘hp’ (horsepower) variable as the predictor. In R, you can create a linear model using the lm() function:

# Use the mtcars dataset
data(mtcars)

# Create a linear model
model <- lm(mpg ~ hp, data = mtcars)

Now that we have our linear model, let’s dive into our first approach for testing homoscedasticity in R: the visual method. We’ll use the ggplot2 package to create a scatter plot of the residuals against the fitted values. To install and load the ggplot2 package, use the following commands:

# Install ggplot2 if not already installed
if (!requireNamespace("ggplot2", quietly = TRUE)) {
  install.packages("ggplot2")
}

# Load ggplot2 package
library(ggplot2)

With ggplot2 loaded, let’s create the scatter plot:

# Check for homoscedasticity using residuals vs fitted values plot
residuals_plot <- ggplot(data = mtcars, aes(x = fitted(model), y = resid(model))) +
  geom_point() +
  geom_smooth(method = "loess", se = FALSE, linetype = "dashed") +
  labs(x = "Fitted Values", y = "Residuals") +
  ggtitle("Residuals vs Fitted Values") +
  theme_minimal()

print(residuals_plot)

The plot shows the residuals (vertical axis) against the fitted values (horizontal axis).

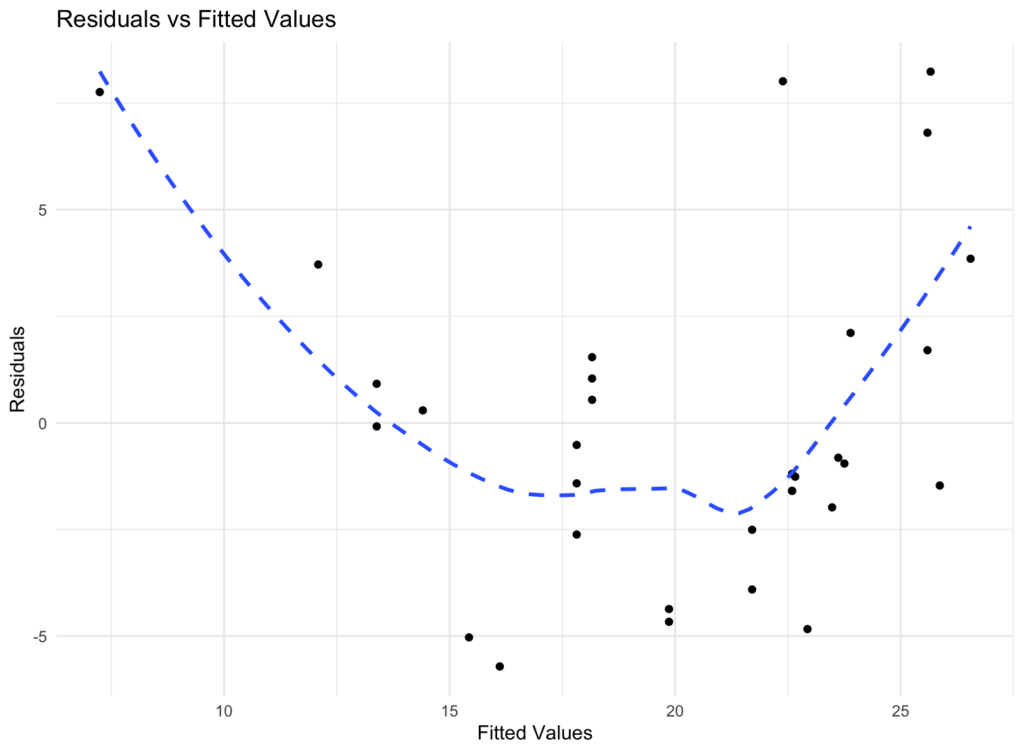
Test Homoscedasticity in R using visual method. Source: uedufy.com

In a homoscedastic scenario, the spread of the residuals should be roughly constant across the range of fitted values. If you see a pattern or a funnel shape in the plot, it might suggest heteroscedasticity (non-constant variance).

Test Homoscedasticity in R using Breusch-Pagan Test

Now, let’s move on to the second approach for testing homoscedasticity in R: the Breusch-Pagan test. This test is a statistical method that examines the relationship between the squared residuals and the fitted values.

To perform the Breusch-Pagan test, we’ll need the ‘car’ package. If you don’t have it installed already, use the following command to install and load it:

# Install car package if not already installed
if (!requireNamespace("car", quietly = TRUE)) {
  install.packages("car")
}

# Load car package
library(car)

With the ‘car’ package loaded, we can now perform the Breusch-Pagan test using the ncvTest() function:

# Perform Breusch-Pagan test to check for homoscedasticity
bp_test <- ncvTest(model)
print(bp_test)

The output of the Breusch-Pagan test includes the Chi-Squared statistic, the degrees of freedom (Df), and the p-value. To interpret the result, compare the p-value to a pre-specified significance level (alpha), usually set at 0.05.

If the p-value is greater than the alpha, you fail to reject the null hypothesis and assume homoscedasticity. If the p-value is less than or equal to alpha, you reject the null hypothesis and assume heteroscedasticity.

You should be getting the following result:

Chisquare = 0.04768862, Df = 1, p = 0.82714

Where:

  • Chisquare (Chi-Squared statistic): This is the test statistic calculated by the Breusch-Pagan test. In your case, it is 0.04768862.
  • Df (Degrees of Freedom): This represents the number of independent parameters in the test. For the Breusch-Pagan test, it is usually 1, as in your case.
  • p (p-value): This is the probability of observing a test statistic as extreme as the one calculated (or more extreme) under the null hypothesis (constant variance). In your case, the p-value is 0.82714.

To interpret the result, we should compare the p-value to a pre-specified significance level (alpha), usually set at 0.05. If the p-value is greater than the alpha, we fail to reject the null hypothesis and assume homoscedasticity. If the p-value is less than or equal to alpha, we reject the null hypothesis and assume heteroscedasticity (non-constant variance).

In your case, the p-value is 0.82714, which is greater than 0.05. Therefore, we fail to reject the null hypothesis, and we can assume homoscedasticity (constant variance) in the residuals of the linear regression model.

Wrapping Up

And there you have it! We’ve covered two popular methods for testing homoscedasticity in R using the mtcars dataset. By mastering these techniques, you can ensure that your linear regression models meet the key assumption of homoscedasticity and produce more reliable results. So, go ahead and give it a try!

Remember, practice makes perfect, and learning how to test homoscedasticity in R is just another step on your journey to becoming a data analysis pro.