Today, we'll dive into something incredibly exciting – how to find a factorial. Before we get into the details, let's briefly discuss factorials and why they matter.
A factorial, typically represented by an exclamation mark (!), is the product of all positive integers up to a given number. For instance, the factorial of 5 (denoted as 5!) is 5 x 4 x 3 x 2 x 1 = 120. Factorials are important in various fields, such as statistics, algebra, calculus, and combinatorics. Plus, they're super fun to work with.
In this blog article, we'll break down how to find a factorial in the simplest way possible. So, buckle up, and let's dive in!
Understanding the Basics: Factorial Formula
Before we explore the process of finding a factorial, let's examine the factorial formula:
n!=n×(n−1)×(n−2)×...×1
Here, n is a non-negative integer. Now, let's break down the factorial formula using a couple of examples:
Example 1: Find 5!
5!=5×4×3×2×1=120
Example 2: Find 7!
7!=7×6×5×4×3×2×1=5,040
Remember that the factorial of 0 (0!) is equal to 1. This might seem a bit strange at first, but it's a convention we follow to make certain calculations easier.
How to Find a Factorial: Step-by-Step Guide
Now that we've got a basic understanding of the factorial formula, let's look at a simple, step-by-step guide on how to find a factorial.
Step 1: Identify the number for which you want to find the factorial
Let's say you want to find the factorial of 6. In this case, the number (n) in the factorial formula above is 6.
Step 2: Start with the number and multiply it by the next smaller number
So, we'll start with 6 and multiply it by the next smaller number, which is 5.
6×5=30
Step 3: Continue multiplying by the next smaller number until you reach 1
6×5×4×3×2×1=720
So, the factorial of 6 (6!) is 720.
Easy, right? Now you know how to find a factorial in no time!
How to Find a Factorial: Advanced Techniques
While the step-by-step guide we just went through works great for smaller numbers, it can become tedious when you're dealing with larger numbers. So, let's explore a couple of advanced techniques to make our lives easier.
How to Find a Factorial in Excel
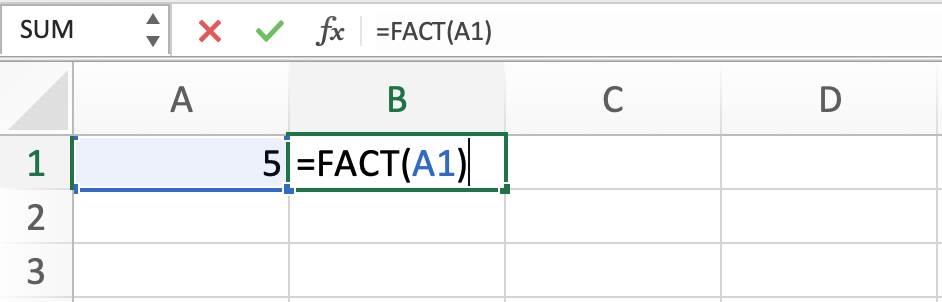
Excel is a powerful tool; you can easily find factorials using the built-in FACT function. Here's how to do it:
Open a new Excel workbook and click on an empty cell where you want the factorial result to appear.
Type the following formula into the cell: =FACT(A1) (assuming the number for which you want to find the factorial is in cell A1).
Press Enter, and the factorial result will be displayed in the cell.
Using the FACT function in Excel to calculate factorial
How to Find a Factorial in R
R is a popular statistical programming language, and finding factorials is a breeze using the built-in factorial() function. Here's how to do it:
Open R or RStudio and create a new script or console.
Type the following code, replacing n with the number for which you want to find the factorial:
n <- 6
result <- factorial(n)
print(result)
Run the script or press Enter in the console, and the factorial result will be displayed.
Using the factorial() function in R to calculate factorial
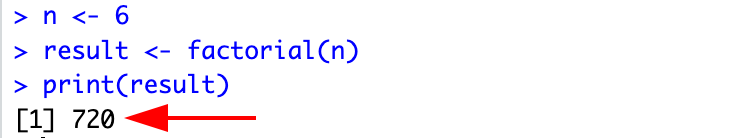
Factorials in Real-Life Applications
Factorials have numerous practical applications, and understanding how to find a factorial can be really helpful. Here are a few examples of where factorials come into play:
Permutations and Combinations: Factorials are used to calculate the number of ways to arrange or choose objects.
Probability: Factorials are used to calculate probabilities in various statistical models.
Taylor Series: Factorials are used in Taylor series expansions, which are essential in calculus and approximating functions.
Queueing Theory: Factorials are used to model complex systems, such as computer networks and traffic patterns.
Frequently Asked Questions
A factorial, denoted by an exclamation mark (!), is the product of all positive integers from 1 up to a given number. For example, 5! (read as 'five factorial') equals 5 × 4 × 3 × 2 × 1 = 120. The factorial of 0 is defined as 1 (0! = 1) by convention. Factorials are fundamental in mathematics and appear frequently in permutations, combinations, probability calculations, and various statistical formulas.
To calculate a factorial by hand, start with your number and multiply it by each consecutive smaller positive integer until you reach 1. For example, to find 6!: Start with 6, then multiply 6 × 5 = 30, then 30 × 4 = 120, then 120 × 3 = 360, then 360 × 2 = 720, and finally 720 × 1 = 720. So 6! = 720. This method works well for smaller numbers but becomes impractical for larger values.
Excel provides a built-in FACT function to calculate factorials easily. To use it: (1) Click on an empty cell where you want the result, (2) Type =FACT(n) where n is either a number or a cell reference containing the number, (3) Press Enter. For example, =FACT(6) returns 720, and =FACT(A1) calculates the factorial of whatever number is in cell A1. This is much faster than manual calculation, especially for larger numbers.
R has a built-in factorial() function that makes calculating factorials simple. To use it, type: n <- 6 (assign your number to a variable), result <- factorial(n) (calculate the factorial), and print(result) to display the answer. For example, factorial(6) returns 720. You can also calculate it directly by typing factorial(6) in the R console. This function handles even very large factorials that would be tedious to calculate manually.
0! = 1 is defined by convention, and while it may seem counterintuitive at first, it's essential for mathematical consistency. This definition makes formulas in combinatorics, probability, and calculus work correctly. For example, the number of ways to arrange 0 objects is 1 (the empty arrangement). Additionally, the factorial function follows the pattern n! = n × (n-1)!, so if we work backwards from 1! = 1, we get 1! = 1 × 0!, which means 0! must equal 1.
Factorials have many practical applications: (1) Permutations and Combinations - calculating the number of ways to arrange or select objects, (2) Probability - computing probabilities in statistical models and distributions, (3) Taylor Series - approximating mathematical functions in calculus, (4) Queueing Theory - modeling systems like computer networks and traffic patterns, and (5) Genetics - calculating genetic variation possibilities. They're essential tools in statistics, computer science, engineering, and data analysis.
Excel's FACT function can calculate factorials up to 170! (170 factorial). Beyond this limit, the result exceeds Excel's numerical precision limits and returns a #NUM! error. 170! equals approximately 7.26 × 10^306, which is an enormously large number. For most practical statistical and mathematical applications, this limit is more than sufficient. If you need to calculate factorials larger than 170, you would need specialized mathematical software or programming languages like Python with special libraries.
Standard factorials are only defined for non-negative integers (0, 1, 2, 3, etc.). You cannot calculate factorial for negative numbers using the traditional definition. For non-integer values (decimals), there's an extension called the Gamma function, where Gamma(n+1) = n! for positive integers. The Gamma function allows factorial-like calculations for real and complex numbers. However, for basic factorial calculations in Excel or R, you should only use non-negative integers.
Wrapping Up
Now you know how to find a factorial like a pro! Whether you're using the step-by-step guide for smaller numbers, Excel, or R for larger numbers, factorials are no longer a mystery.
Remember, factorials are not just a fun math exercise – they're an essential tool in many different fields such as statistics. So, next time you encounter a problem involving factorials, you'll know exactly how to tackle it.
Using the FACT function in Excel to calculate factorial
Using the factorial() function in R to calculate factorial