How To Calculate Multiple Linear Regression Using SPSS

In this statistics lesson, we will learn how to calculate multiple linear regression using SPSS and interpret multiple linear regression output in SPSS. I will also provide you with an SPSS dataset for multiple linear regression analysis so you can practice everything we cover in this lesson.

Analyzing a multiple linear regression in SPSS is very simple. Is so straightforward that if you know how to calculate a simple linear regression in SPSS, you won’t have any trouble with your analysis for multiple linear regression.

The result interpretation is slightly different as the model contains more variables, but don’t worry, we will cover every parameter in the regression output here.

Ready? Let’s get started.

What is Multiple Linear Regression Explained with Example

With simple linear regression, we analyze the causal relationship between a single independent variable and a dependent variable. In other words, we aim to see if the independent variable (predictor) has a significant effect on the dependent variable (outcome). But how do we analyze regression when a model contains multiple independent variables?

Say hello to multiple linear regression analysis.

In multiple linear regression analysis, we test the effect of two or more predictors on the outcome variable, hence the term multiple linear regression. 

In terms of analysis, for both simple and multiple linear regression the goal remains pretty much the same: finding if there is any significance (P-value) between the multiple predictors and outcome. If the P-value is equal to or lower than 0.05 (P ≤ 0.05) the predictor-outcome relationship is significant. 

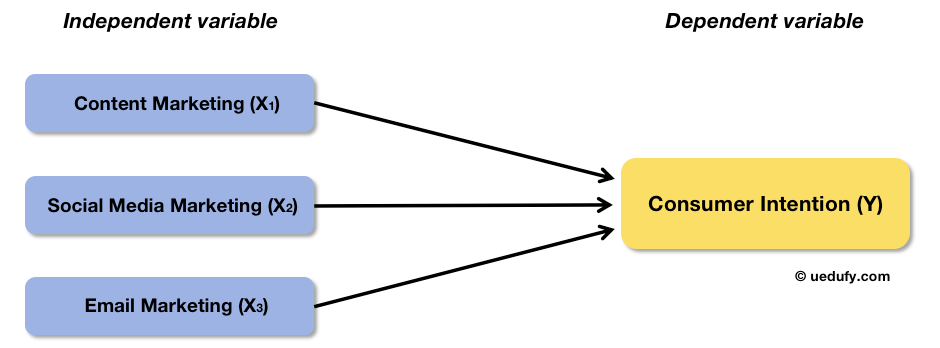
Let’s look at an example of multiple linear regression. Suppose we want to investigate the relationship between marketing efforts and consumer purchase intention of a company. In this case, the predictor variable is marketing efforts and the outcome is purchase intention.

I know what you’re thinking. “Marketing efforts” is such a broad term and so many factors can contribute to it. There’s no point investigating marketing efforts as a whole if we can’t identify which factors are more important than others, right? 

Let’s split marketing efforts into several independent variables (X), e.g., content marketing (X₁), social media marketing (X₂), and email marketing (X₃). Here is what the conceptual framework for this example looks like:

Now that we got our conceptual framework, let’s jump into action and do multiple regression analysis in SPSS using the example we discussed above. 

Calculate Multiple Linear Regression using SPSS

Calculating multiple linear regression using SPSS is very much the same as doing a simple linear regression analysis in SPSS. If you want to follow along, download the SPSS dataset below.

Unzip the file and double-click on the file with the .sav extension to import the data set in SPSS. The example SPSS data set contains 30 samples where the Content, SocialMedial, Email are independent variables (predictors), and Consumer_Intention is the dependent variable (outcome).

Next, let’s learn how to calculate multiple linear regression using SPSS for this example.

1. In SPSS top menu, go to Analyze → Regression → Linear. 

2. On the Linear Regression window, use the arrow button to move the outcome Consumer_Intention to the Dependent box. Do the same with the predictor variables Email, Content, and SocialMedia to move them to the Independent(s) box. 

Make sure the linear regression method is set to Enter.

Click the OK button to calculate multiple linear regression using SPSS. A new window containing the multiple liner regression results will appear.

Interpret Multiple Linear Regression Output in SPSS

Now we got our multiple linear regression results in SPSS, let’s look at how to interpret the output. By default, SPSS will show four tables in the regression output:

Let’s have a look at each table and understand what those terms and values mean.

1. Variables Entered/Removed

This table contains an analysis summary of the multiple linear regression using SPSS respectively the regression model used, the independent and dependent variables entered in analysis, as well as the regression method. 

In some cases, SPSS will choose to remove variables from the model if they are found to cause multicollinearity issues. In this regression analysis, no variables were removed therefore we can deduct that no variables were found to be linearly dependent on one another. 

2. ANOVA

The one-way ANOVA test is a statistical technique that compares the level of variance between groups of observations to the variability within those groups. The multiple linear regression ANOVA works by examining the variations in the mean value of the dependent variable when changes in the independent variable occur. 

Let’s start with the Sum of Squares column in ANOVA.  The Regression Sum of Squares shows the amount of variation that occurs between the independent and dependent variables. In our case, the variation attributed to the relationship between predictors Email, Content, and SocialMedia and Consumer_Intention respectively 2.952. You should aim at values as closer to as zero as possible meaning that your data is a good fit for the regression model

The Residual Sum of Squares measures the variation attributed to the error in the model. In our case, the Residual Sum of Squares is 3.715 which is high. You should aim here at values as low as possible where zero means that your regression model is a perfect fit for the data.

The Total Sum of Squares is calculated by adding the Regression Sum of Squares and Residual Sum of Squares respectively 6.667 in our case.

Next, let’s look at the Degree of Freedom (df) column in ANOVA respectively Regression, Residual and Total Degree of Freedom. 

The Regression df refers to the number of observations in a data set that has the freedom to vary. The Residual df refers to the remaining amount of observations in a data set that could be used to generate a new similar model. Remember that the larger the sample size the higher the degree of freedom. In our case, the regression df is 3 and the residual df is 26.

The Regression Mean Square is calculated by dividing the regression sum of squares divided by the regression degree of freedom – in our example 0.984. The Residual Mean Square is computed in the same way, by dividing the residual sum of squares by the residual degree of freedom – respectively, 0.143 in our case. 

The F column in ANOVA represents the F statistics which is probably the most important quantity in the ANOVA test. The F statistics equals the ratio between Regression Mean Square and Residual Mean Square and is used to calculate the P-value. In our example, the F statistics equals 6.887

Finally, the Sig. column in ANOVA (P-value) tells us if the difference between the groups in the regression model is significant. Since in our case the P is 0.001 respectively ≤ 0.05, the difference between Content, SocialMedia, and Email groups are statistically significant.

3. Coefficients

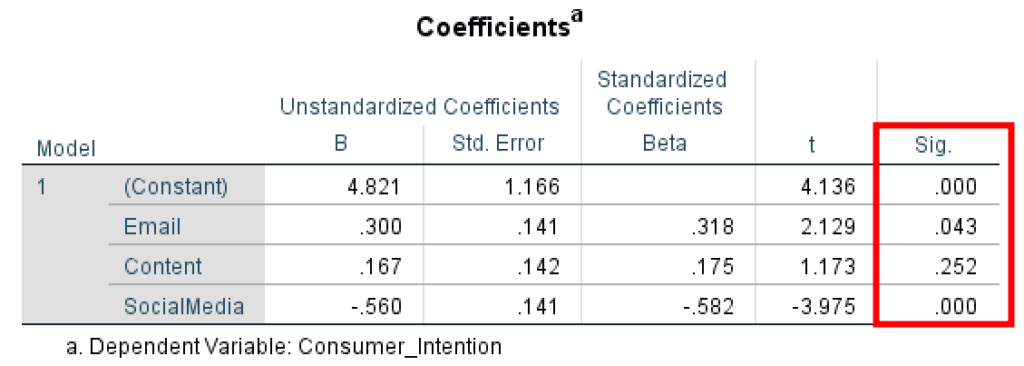
The last table in the regression output is the Coefficients table. Here we can find details about the Unstandardized Coefficient Beta and Standard Error, Standardized Coefficient Beta, the t and P-value the predictors in our model.

The Unstandardized Coefficient Beta measures the variation in the outcome variable for one unit of change in the predictor variable, where the raw values are displayed in the original scale.

The Standard Error of the estimates measures the average distance of the observed data points from the regression line. A large standard error value indicates that sample means are distributed widely around the population mean. A low standard error value indicates that the mean of the sample and the mean of the population are closely correlated – a good thing.

The Standardized Coefficients Beta also known as beta weights or beta coefficients measures the variations in the predictor and outcome variables where the underlying values have been standardized to equal to 1.

The t statistics column shows the measure of the standard deviation of the coefficient and is calculated by dividing the Beta coefficient by its standard error. In general, a value larger than +2 or -2 is considered acceptable. 

Finally, the Sig. (P-value) column in the regression coefficients shows the statistical significance for each predictor on the outcome variable where a P-value ≤ 0.05 is considered acceptable. 

In our example, we can observe that the predictor variable Email has an effect on the outcome variable Consumer_Intention (P = 0.043, < 0.05) therefore the relationship is statistically significant.

The predictor Content has no effect on the outcome Consumer_Intention (P =  0.252, > 0.05) therefore no statistical significance in the regression model.

The predictor SocialMedia has an effect on the Consumer_Intention (P =  0.000, < 0.05) therefore the relationship between the two variables is statistically significant. 

In conclusion, the most important values you should check when looking to interpret multiple linear regression output in SPSS are:

• One-way ANOVA test results tell us if the difference between the groups in the regression model is significant at P ≤ 0.05.
• Regression coefficient showing a significant effect between predictor and outcome variable at P ≤ 0.05.

Export Linear Regression Output in SPSS

Finally, let’s export the multiple linear regression using SPSS results as a .pdf file for further use. On the regression results Output window, click on File → Export.

1. In the Export Output window, select the Portable Document Format (*.pdf) option. Other options such as Word/RTF (.doc) and PowerPoint (.ppt) export options are available in case you prefer those formats.
2. Type a File Name and Browse for the location you prefer to save your multiple linear regression results in SPSS.
3. Click the OK button to export the SPSS output.

The file containing the multiple linear regression output in SPSS is now available for your further use. 

Wrapping Up

I hope by now you got an understanding of how to calculate multiple linear regression using SPSS as well as how to interpret multiple linear regression output in SPSS. As you can see, is not that difficult.

If this is the first time you perform a linear regression in SPSS, I recommend you to repeat the process a few times more as well as try using your dataset for multiple linear regression analysis.