Mean Median Mode คืออะไร? วิธีคำนวณค่าเฉลี่ย ค่ามัธยฐาน ค่าฐานนิยม และความสัมพันธ์

•By Natcharee Chaisirijirasin•th
สถิติExcelR Programming

Mean, Median และ Mode เป็นสามหลักการพื้นฐานของ Measures of Central Tendency ในสถิติที่ช่วยให้คุณเข้าใจค่ากลางหรือค่าแทนในชุดข้อมูล ไม่ว่าคุณจะวิเคราะห์คะแนนสอบ ยอดขาย หรือผลการสำรวจ สถิติเหล่านี้ให้มุมมองที่แตกต่างกันเกี่ยวกับสิ่งที่ถือว่า "ปกติ" หรือ "เฉลี่ย" ในข้อมูลของคุณ

ในคู่มือนี้ คุณจะได้เรียนรู้วิธีคำนวณ Mean, Median และ Mode ด้วยตัวเองโดยใช้สูตรง่ายๆ จากนั้นค้นพบวิธีที่เร็วกว่าด้วยฟังก์ชัน Excel และการเขียนโปรแกรม R แต่ละตัววัดมีจุดแข็งที่ไม่เหมือนกัน และเมื่อจบบทเรียนนี้ คุณจะรู้ว่าเมื่อไหร่ควรใช้แต่ละตัววัด

วิธีคำนวณค่าเฉลี่ย (Mean) ในสถิติ

Mean (ค่าเฉลี่ยเลขคณิต) คำนวณได้โดยนำค่าทั้งหมดในชุดข้อมูลมารวมกัน แล้วหารด้วยจำนวนค่าทั้งหมด เป็นตัววัด Measure of Central Tendency ที่ใช้กันมากที่สุด

สูตร:

Mean=∑xn\Large \text{Mean} = \frac{\sum x}{n}

โดยที่ Σx คือผลรวมของค่าทั้งหมด และ n คือจำนวนค่า

ตัวอย่าง:

สมมติว่าคุณเป็นครูที่กำลังคำนวณคะแนนเฉลี่ยของการสอบในชั้นเรียน คะแนนมีดังนี้:

89,76,95,82,68,91,7889, 76, 95, 82, 68, 91, 78

ขั้นตอนที่ 1: รวมคะแนนทั้งหมดเข้าด้วยกัน:

89+76+95+82+68+91+78=57989 + 76 + 95 + 82 + 68 + 91 + 78 = 579

ขั้นตอนที่ 2: หารด้วยจำนวนคะแนน (7):

579÷7=82.7579 \div 7 = 82.7

ค่าเฉลี่ยคะแนนสอบคือ 82.7 คะแนน

คำนวณค่าเฉลี่ย (Mean) ใน Excel

ฟังก์ชัน AVERAGE ของ Excel ทำให้การคำนวณค่าเฉลี่ยรวดเร็วและง่ายดาย:

  1. คลิกที่เซลล์ว่างที่คุณต้องการให้แสดงผลลัพธ์
  2. พิมพ์ =AVERAGE( ลงในเซลล์
  3. เลือกช่วงของเซลล์ที่มีข้อมูลของคุณ (เช่น A1:A10)
  4. ปิดวงเล็บและกด Enter

ตัวอย่าง:

=AVERAGE(A1:A10)

สำหรับฟังก์ชันสถิติเพิ่มเติมใน Excel ตรวจสอบคู่มือของเราเกี่ยวกับ Descriptive Statistics ใน Excel

คำนวณค่าเฉลี่ย (Mean) ใน R

R มีฟังก์ชัน mean() ในตัวสำหรับการคำนวณอย่างรวดเร็ว:

# สร้าง vector ด้วยข้อมูลตัวอย่าง
data <- c(10, 20, 30, 40, 50)
 
# คำนวณค่าเฉลี่ย
mean_value <- mean(data)
 
# แสดงผลลัพธ์
print(mean_value)
# Output: 30

ค่าเฉลี่ยคือ 30 (ผลรวม 150 หารด้วย 5 ค่า)

วิธีคำนวณค่าฐานนิยม (Mode) ในสถิติ

Mode คือค่าที่ปรากฏบ่อยที่สุดในชุดข้อมูล ไม่เหมือนกับ Mean และ Median ชุดข้อมูลสามารถมี:

  • Mode เดียว (unimodal)
  • หลาย Mode (bimodal หรือ multimodal)
  • ไม่มี Mode (ค่าทั้งหมดปรากฏด้วยความถี่เท่ากัน)

ตัวอย่าง:

สมมติว่าคุณเป็นเจ้าของร้านขายรองเท้าและต้องการหาเบอร์รองเท้าที่พบบ่อยที่สุด ลูกค้า 20 คนล่าสุดของคุณซื้อรองเท้าเบอร์เหล่านี้:

7,8,9,7,10,9,8,7,11,10,9,7,9,8,8,10,7,9,8,107, 8, 9, 7, 10, 9, 8, 7, 11, 10, 9, 7, 9, 8, 8, 10, 7, 9, 8, 10

นับความถี่:

เบอร์รองเท้าความถี่
75 ครั้ง
85 ครั้ง
96 ครั้ง
104 ครั้ง
111 ครั้ง

Mode คือ เบอร์ 9 (ปรากฏ 6 ครั้ง มากกว่าเบอร์อื่นๆ)

คำนวณค่าฐานนิยม (Mode) ใน Excel

Excel มีฟังก์ชัน Mode สองแบบ:

Mode เดียว (Unimodal Data)

ใช้ MODE.SNGL สำหรับชุดข้อมูลที่มีค่าที่พบบ่อยที่สุดค่าเดียว:

=MODE.SNGL(A1:A10)

หลาย Mode (Multimodal Data)

ใช้ MODE.MULT สำหรับชุดข้อมูลที่มีค่าที่พบบ่อยที่สุดหลายค่า:

=MODE.MULT(A1:A10)

เพื่อแสดง Mode ทั้งหมด ให้ใส่สูตรและกด Ctrl+Shift+Enter (array formula) จากนั้นคัดลอกไปยังเซลล์ที่อยู่ติดกัน

คำนวณค่าฐานนิยม (Mode) ใน R

R ไม่มีฟังก์ชัน Mode ในตัว แต่คุณสามารถคำนวณได้ง่ายๆ:

# สร้าง vector
shoe_sizes <- c(7, 8, 9, 7, 10, 9, 8, 7, 11, 10, 9, 7, 9, 8, 8, 10, 7, 9, 8, 10)
 
# คำนวณ mode
mode_value <- as.numeric(names(which.max(table(shoe_sizes))))
 
# แสดงผลลัพธ์
print(mode_value)
# Output: 9

วิธีคำนวณค่ามัธยฐาน (Median) ในสถิติ

Median คือค่ากลางเมื่อจัดเรียงค่าทั้งหมดจากน้อยไปมากหรือจากมากไปน้อย มันแบ่งชุดข้อมูลออกเป็นสองส่วน โดยมี 50% ของค่าต่ำกว่า Median และ 50% สูงกว่า

Median มีความทนทานต่อค่าผิดปกติ (outliers) มากกว่า Mean ทำให้เป็นประโยชน์สำหรับข้อมูลที่เบ้

สูตร:

  • จำนวนค่าคี่: Median คือค่ากลาง
  • จำนวนค่าคู่: Median คือค่าเฉลี่ยของสองค่ากลาง

ตัวอย่าง:

คุณกำลังวิเคราะห์รายได้ครัวเรือน (หน่วยพันดอลลาร์) ในย่าน:

45,60,70,55,80,90,65,75,5045, 60, 70, 55, 80, 90, 65, 75, 50

ขั้นตอนที่ 1: จัดเรียงจากน้อยไปมาก:

45,50,55,60,65,70,75,80,9045, 50, 55, 60, 65, 70, 75, 80, 90

ขั้นตอนที่ 2: หาค่ากลาง (ตำแหน่งที่ 5 ใน 9 ค่า):

Median คือ 65 (ค่ากลางที่แท้จริงที่มี 4 ค่าด้านล่างและ 4 ค่าด้านบน)

คำนวณค่ามัธยฐาน (Median) ใน Excel

ใช้ฟังก์ชัน MEDIAN ของ Excel:

  1. คลิกเซลล์ว่าง
  2. พิมพ์ =MEDIAN(
  3. เลือกช่วงข้อมูลของคุณ (เช่น A1:A10)
  4. ปิดวงเล็บและกด Enter

ตัวอย่าง:

=MEDIAN(A1:A10)

คำนวณค่ามัธยฐาน (Median) ใน R

ฟังก์ชัน median() ในตัวของ R คำนวณ Median:

# สร้าง vector
data <- c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10)
 
# คำนวณ median
data_median <- median(data)
 
# แสดงผลลัพธ์
print(data_median)
# Output: 5.5

เมื่อมี 10 ค่า (จำนวนคู่) Median คือค่าเฉลี่ยของค่าที่ 5 (5) และที่ 6 (6):

(5+6)/2=5.5(5 + 6) / 2 = 5.5

การแสดงภาพ Mean, Mode และ Median ใน R

นี่คือโค้ด R สำหรับแสดงภาพตัววัดทั้งสามบน Histogram โดยใช้ตัวอย่างเบอร์รองเท้า:

# โหลด library ที่ต้องการ
library(ggplot2)
 
# ชุดข้อมูล
shoe_sizes <- c(7, 8, 9, 7, 10, 9, 8, 7, 11, 10, 9, 7, 9, 8, 8, 10, 7, 9, 8, 10)
 
# คำนวณ mean, mode และ median
mean_size <- mean(shoe_sizes)
mode_size <- as.numeric(names(which.max(table(shoe_sizes))))
median_size <- median(shoe_sizes)
 
# สร้าง histogram พร้อมเส้นแนวตั้ง
hist_plot <- ggplot(data.frame(shoe_sizes), aes(shoe_sizes)) +
  geom_histogram(binwidth = 1, fill = "lightblue", color = "black") +
  geom_vline(aes(xintercept = mean_size), color = "blue",
             linetype = "dashed", size = 1.5) +
  geom_vline(aes(xintercept = mode_size), color = "red",
             linetype = "dashed", size = 1.5) +
  geom_vline(aes(xintercept = median_size), color = "green",
             linetype = "dashed", size = 1.5) +
  labs(title = "Shoe Size Distribution",
       subtitle = "Mean (blue), Mode (red), Median (green)",
       x = "Shoe Size",
       y = "Frequency") +
  theme_minimal()
 
# แสดง plot
print(hist_plot)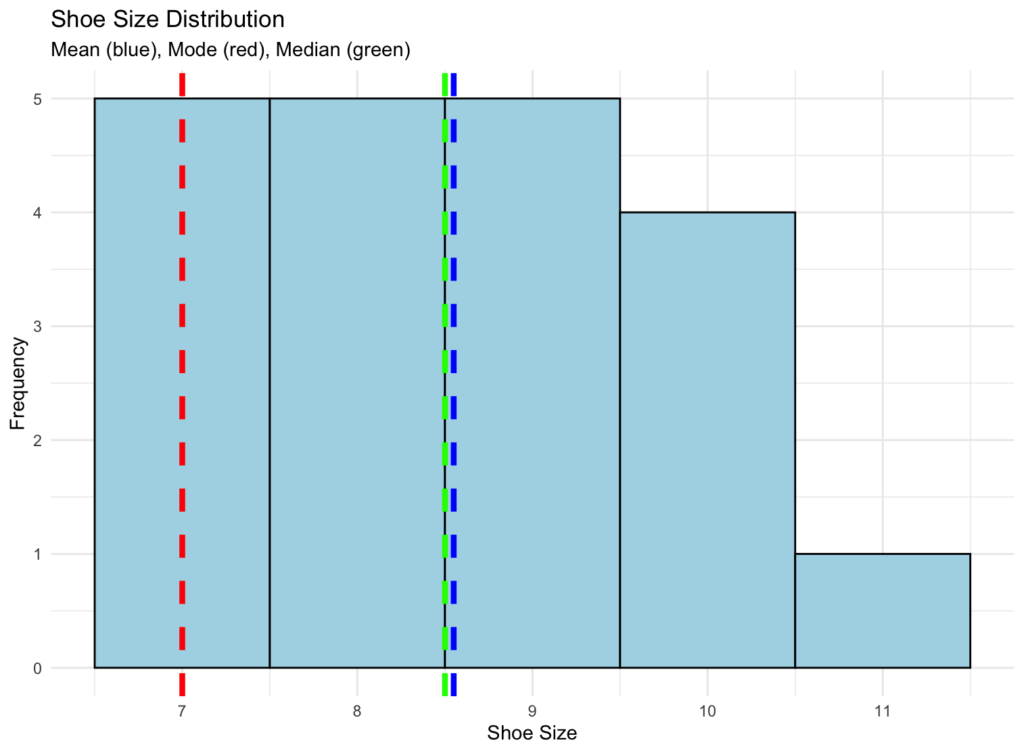

กราฟ Histogram แสดงการกระจายของเบอร์รองเท้าพร้อมเส้นแนวตั้งแสดง Mean สีน้ำเงิน, Mode สีแดง และ Median สีเขียว การแสดงภาพ Mean, Mode และ Median บน Histogram

การแสดงภาพนี้ช่วยให้คุณเห็นว่าตัววัดทั้งสามนี้เกี่ยวข้องกับการกระจายข้อมูลของคุณอย่างไร Mode ปรากฏที่จุดสูงสุด (ค่าที่พบบ่อยที่สุด) ในขณะที่ Mean และ Median แสดงแง่มุมที่แตกต่างของศูนย์กลางข้อมูล

ความสัมพันธ์ระหว่าง Mean, Median และ Mode

ความสัมพันธ์ระหว่าง Mean, Median และ Mode เปิดเผยข้อมูลสำคัญเกี่ยวกับการกระจายและความเบ้ของข้อมูลของคุณ

ใน Symmetric Distribution (การกระจายแบบสมมาตร)

เมื่อข้อมูลสมมาตรอย่างสมบูรณ์และมีการกระจายแบบปกติ (โค้งรูประฆัง):

Mean=Median=Mode\Large \text{Mean} = \text{Median} = \text{Mode}

ตัววัดทั้งสามมาบรรจบกันที่ศูนย์กลางของการกระจาย นี่เป็นสถานการณ์ที่เหมาะสมที่สุดสำหรับการวิเคราะห์ทางสถิติส่วนใหญ่

ตัวอย่าง: ความสูงของผู้ชายผู้ใหญ่มักจะมีการกระจายแบบปกติที่ความสูงเฉลี่ย (Mean) ความสูงกลาง (Median) และความสูงที่พบบ่อยที่สุด (Mode) ล้วนใกล้เคียงกันทั้งหมด

ใน Right-Skewed Distribution (การกระจายเบ้ขวา - Positively Skewed)

เมื่อข้อมูลมีหางยาวไปทางขวา (พบบ่อยในรายได้ ราคาบ้าน):

Mode<Median<Mean\Large \text{Mode} < \text{Median} < \text{Mean}

Mean ถูกดึงไปทางหางโดยค่าสูงมากๆ ในขณะที่ Median อยู่ตรงกลาง และ Mode อยู่ที่จุดสูงสุด

ตัวอย่าง: การกระจายรายได้ครัวเรือน

  • Mode: $45,000 (รายได้ที่พบบ่อยที่สุด)
  • Median: $65,000 (ค่ากลาง)
  • Mean: $85,000 (ถูกดึงขึ้นโดยผู้มีรายได้สูง)

ใน Left-Skewed Distribution (การกระจายเบ้ซ้าย - Negatively Skewed)

เมื่อข้อมูลมีหางยาวไปทางซ้าย:

Mean<Median<Mode\Large \text{Mean} < \text{Median} < \text{Mode}

Mean ถูกดึงไปทางหางโดยค่าต่ำมากๆ

ตัวอย่าง: คะแนนสอบที่นักเรียนส่วนใหญ่ได้คะแนนสูง (90) แต่มีบางคนได้คะแนนต่ำมาก

สูตรความสัมพันธ์เชิงประจักษ์ (Empirical Relationship)

สำหรับการกระจายที่เบ้ปานกลาง มีความสัมพันธ์โดยประมาณ:

Mean−Mode≈3(Mean−Median)\Large \text{Mean} - \text{Mode} \approx 3(\text{Mean} - \text{Median})

ความสัมพันธ์เชิงประจักษ์นี้สามารถช่วยคุณประมาณตัววัดหนึ่งเมื่อคุณรู้อีกสองตัว แม้ว่าจะแม่นยำที่สุดสำหรับการกระจายแบบ Unimodal ที่เบ้ปานกลาง

เมื่อไหร่ควรใช้ Mean, Mode หรือ Median

แต่ละตัววัด Measure of Central Tendency มีกรณีใช้งานเฉพาะ:

ใช้ Mean เมื่อ:

  • ข้อมูลมีการกระจายแบบปกติ (สมมาตร รูประฆัง)
  • คุณต้องการพิจารณาค่าทั้งหมดในชุดข้อมูล
  • ทำการคำนวณทางสถิติเพิ่มเติม (Standard Deviation, Variance)

ใช้ Median เมื่อ:

  • ข้อมูลมีค่าผิดปกติหรือค่าสุดโต่ง
  • ข้อมูลเบ้ (ไม่มีการกระจายแบบปกติ)
  • วิเคราะห์รายได้ ราคาบ้าน หรือข้อมูลที่เบ้ขวาอื่นๆ
  • คุณต้องการตัววัดที่ทนต่อค่าสุดโต่ง

ใช้ Mode เมื่อ:

  • วิเคราะห์ข้อมูลเชิงหมวดหมู่ (สี ขนาด หมวดหมู่)
  • หาค่าที่พบบ่อยที่สุดหรือนิยมที่สุด
  • ข้อมูลมีหลายยอด (Bimodal หรือ Multimodal Distribution)
  • ทำงานกับข้อมูลแบบไม่ต่อเนื่อง (เบอร์รองเท้า จำนวนลูก)

สำหรับความเข้าใจที่ลึกซึ้งยิ่งขึ้นเกี่ยวกับแนวคิดเหล่านี้ อ่านบทความของเราเกี่ยวกับ Measure of Central Tendency คืออะไร

คำถามที่พบบ่อย

สรุป

การคำนวณ Mean, Mode และ Median เป็นพื้นฐานสำหรับการทำความเข้าใจข้อมูลของคุณ แต่ละตัววัดให้ข้อมูลเชิงลึกที่ไม่เหมือนกันเกี่ยวกับ Central Tendency และการรู้ว่าเมื่อไหร่ควรใช้แต่ละตัวเป็นสิ่งสำคัญสำหรับการวิเคราะห์ข้อมูลที่แม่นยำ

ไม่ว่าคุณจะคำนวณตัววัดเหล่านี้ด้วยตัวเองสำหรับชุดข้อมูลขนาดเล็ก ใช้ฟังก์ชัน Excel สำหรับการวิเคราะห์อย่างรวดเร็ว หรือใช้ประโยชน์จาก R สำหรับงานทางสถิติที่ซับซ้อน เครื่องมือเหล่านี้เป็นรากฐานของ Descriptive Statistics การทำความเข้าใจ Standard Deviation และ Variance จะช่วยเพิ่มพูนทักษะการวิเคราะห์ทางสถิติของคุณต่อไป

ฝึกฝนกับชุดข้อมูลที่แตกต่างกันเพื่อพัฒนาสัญชาตญาณเกี่ยวกับว่าตัววัดใดแทน Central Tendency ของข้อมูลของคุณได้ดีที่สุด