Regresia liniară multiplă (multiple linear regression) extinde regresia simplă permițându-ți să prezici un rezultat folosind două sau mai multe variabile predictor simultan. Acest lucru este esențial pentru cercetarea de licență unde fenomenele din lumea reală sunt rareori explicate de un singur factor. Fie că prezici performanța academică pe baza obiceiurilor de studiu, somnului și frecvenței, fie că prognozezi vânzările din publicitate, prețuri și sezonalitate, regresia multiplă dezvăluie care predictori contează cel mai mult și cum funcționează împreună.
Spre deosebire de regresia simplă care răspunde la "Prezice X pe Y?", regresia multiplă răspunde la întrebarea mai realistă: "Prezic X₁, X₂ și X₃ împreună pe Y, și care predictor are cel mai puternic efect?" Acest lucru o face una dintre cele mai utilizate tehnici statistice în cercetarea de disertație din psihologie, educație, afaceri, științe ale sănătății și științe sociale.
Acest ghid cuprinzător îți arată cum să efectuezi regresia liniară multiplă în Excel folosind Analysis ToolPak, să interpretezi corect rezultatele (inclusiv R² ajustat și semnificația predictorilor individuali), să detectezi problemele de multicolinearitate, să verifici asumpțiile și să raportezi constatările în format APA ediția a 7-a. Vei învăța și limitările critice ale Excel și când ai nevoie de SPSS sau R în schimb.
Idei cheie:
- Regresia multiplă prezice Y din 2+ variabile predictor simultan
- Raportează întotdeauna R² ajustat (nu R² obișnuit) pentru că acesta corectează pentru numărul de predictori
- Verifică multicolinearitatea mai întâi folosind matricea de corelație (predictorii ar trebui să aibă r < 0.80)
- Un model general semnificativ (testul F) nu înseamnă că toți predictorii individuali sunt semnificativi
- Excel gestionează bine regresia multiplă standard dar nu poate face regresie stepwise, ierarhică sau logistică
Înainte de a începe: Acest ghid presupune că înțelegi regresia liniară simplă - citește mai întâi acel ghid dacă ești nou în regresie. Vei avea nevoie și de Excel cu Analysis ToolPak instalat. Dacă nu l-ai activat încă, vezi ghidul nostru despre cum să activezi Data Analysis în Excel.
Ce este Regresia Liniară Multiplă?
Regresia liniară multiplă (multiple linear regression) este o metodă statistică care modelează relația dintre două sau mai multe variabile independente (predictori, X₁, X₂, X₃...) și o variabilă dependentă (rezultat, Y) prin potrivirea unei ecuații liniare la datele observate. Extinde regresia simplă pentru a ține cont de mai mulți factori care ar putea influența rezultatul tău.
Ecuația Regresiei Multiple
Dacă ai citit manuale de statistică sau ai urmărit tutoriale, poate ai observat formula de regresie scrisă diferit în funcție de sursă. Nu-ți face griji - ambele versiuni sunt corecte! Diferența este pur și simplu o convenție de notație, și înțelegerea ambelor te va ajuta să citești orice resursă de statistică cu încredere.
În manualele de statistică teoretică, vei vedea de obicei litere grecești (simboluri beta). Această notație reprezintă adevărații parametri ai populației - valorile "reale" care există în întreaga populație pe care încercăm să o estimăm:
În ghidurile aplicate și tutorialele Excel (inclusiv acesta), vei vedea adesea litere romane (a și b). Această notație reprezintă estimările din eșantion - valorile reale pe care Excel le calculează din datele tale ca estimări ale acelor parametri ai populației:
Concluzia: Când vezi β₀ într-un manual și "Intercept" în Excel, se referă la același lucru. Când profesorul tău scrie β₁ pe tablă și Excel arată un coeficient de 2.15, este același concept. Excel etichetează rezultatul său simplu ca "Coefficients" indiferent de ce notație folosește manualul tău.
Unde:
- Y = Variabila dependentă (ce prezici)
- X₁, X₂, X₃ = Variabile independente (predictorii tăi)
- β₀ sau a = Interceptul (valoarea Y așteptată când toate variabilele X = 0)
- β₁, β₂, β₃ sau b₁, b₂, b₃ = Coeficienți de pantă (schimbarea în Y pentru fiecare creștere de 1 unitate în acel X, menținând ceilalți predictori constanți)
- ε = Termen de eroare (variație neexplicată)
De exemplu, dacă prezici scorurile la examen din orele de studiu, somn și frecvența la cursuri:
Aceasta înseamnă: Fiecare oră suplimentară de studiu crește scorul la examen cu 1.75 puncte (menținând somnul și frecvența constante), fiecare oră suplimentară de somn adaugă 0.52 puncte, și fiecare curs suplimentar frecventat adaugă 2.36 puncte.
Avantajul Cheie: "Menținând Celelalte Variabile Constante"
Expresia "menținând celelalte variabile constante" (numită și "controlând pentru") este ceea ce face regresia multiplă puternică. În regresia simplă, dacă orele de studiu prezic scorurile la examen, nu poți spune dacă sunt cu adevărat orele de studiu sau ceva corelat cu ele (cum ar fi frecvența). Regresia multiplă separă aceste efecte:
- Regresia simplă: "Studenții care studiază mai mult au scoruri mai mari" (dar poate frecventează și mai multe cursuri)
- Regresia multiplă: "Studenții care studiază mai mult au scoruri mai mari, chiar când ținem cont de frecvența lor"
Aceasta îți permite să izolezi contribuția unică a fiecărui predictor - esențial pentru a face argumente cauzale în capitolul de Discuții al lucrării tale.
Când să Folosești Regresia Liniară Multiplă pentru Lucrarea Ta
Folosește regresia liniară multiplă când cercetarea ta îndeplinește aceste criterii:
1. Cerințe pentru Întrebarea de Cercetare:
- Vrei să prezici Y folosind mai mulți factori simultan
- Vrei să controlezi pentru variabilele confundate
- Vrei să determini care predictori contează cel mai mult
- Vrei să compari importanța relativă a diferiților predictori
2. Cerințe pentru Variabile:
- Doi sau mai mulți predictori continui (X₁, X₂, etc.): Scală interval sau raport
- Un rezultat continuu (Y): Scală interval sau raport
- Dimensiunea minimă a eșantionului: n ≥ 50 + 8k (unde k = numărul de predictori)
3. Exemple de Cercetare pe Discipline:
- Psihologie: Prezic orele de terapie, aderența la medicație ȘI suportul social reducerea depresiei?
- Educație: Prezic orele de studiu (Study_Hours), calitatea somnului (Sleep_Hours) ȘI frecvența la cursuri (Classes_Attended) scorurile la examen (Exam_Score)?
- Afaceri: Prezic bugetul de publicitate, prețul ȘI activitatea concurenței veniturile din vânzări?
- Științe ale Sănătății: Prezic exercițiul, calitatea dietei ȘI aderența la medicație pierderea în greutate?
- Științe Sociale: Prezic venitul, educația ȘI rețelele sociale satisfacția vieții?
Regresie Liniară Simplă vs Multiplă: Care Îți Trebuie?
Înainte de a continua, asigură-te că regresia multiplă este alegerea potrivită pentru întrebarea ta de cercetare:
Figura 1: Diagramă de decizie pentru selectarea regresiei liniare simple (un predictor) sau regresiei liniare multiple (doi sau mai mulți predictori) bazată pe întrebarea ta de cercetare
| Caracteristică | Regresie Liniară Simplă | Regresie Liniară Multiplă |
|---|---|---|
| Număr de predictori | 1 variabilă independentă | 2 sau mai multe variabile independente |
| Ecuația | Y = a + bX | Y = a + b₁X₁ + b₂X₂ + b₃X₃... |
| Întrebarea de cercetare | "Prezice timpul de studiu scorurile la examen?" | "Prezic timpul de studiu, somnul ȘI frecvența împreună scorurile la examen?" |
| Controlează pentru confunderi | Nu | Da - izolează efectele unice |
| Compară importanța predictorilor | N/A (doar un predictor) | Da - care predictor contează cel mai mult? |
| Statistică cheie | R² | R² ajustat (corectează pentru numărul de predictori) |
| Asumpție suplimentară | Niciuna | Fără multicolinearitate între predictori |
| Capabilitate Excel | Suport complet | Suport complet (dar fără calcul VIF) |
Tabel 1: Comparație Regresie Liniară Simplă vs. Multiplă
Folosește Regresia Liniară Simplă când:
- Ai doar o singură variabilă predictor
- Întrebarea ta de cercetare se concentrează pe o singură relație specifică
- Faci analiză preliminară înainte de a adăuga mai mulți predictori
- Exemplu: "Prezice bugetul de publicitate vânzările?"
Folosește Regresia Liniară Multiplă când:
- Ai două sau mai multe variabile predictor
- Vrei să controlezi pentru variabilele confundate
- Trebuie să compari importanța relativă a predictorilor
- Testezi un model teoretic cu mai mulți factori
- Exemplu: "Prezic bugetul de publicitate, prețul ȘI sezonalitatea împreună vânzările, și care contează cel mai mult?"
Întrebare de cercetare diferită? Dacă compari mediile grupurilor în loc să prezici un rezultat continuu, vezi ghidul nostru despre alegerea între T-Test și ANOVA.
Set de Date Eșantion pentru Acest Tutorial
Pe parcursul acestui ghid, vom folosi un set de date realist de licență care examinează cum mai mulți factori prezic performanța la examen pentru 30 de studenți universitari. Acest lucru demonstrează o întrebare tipică de cercetare: "Prezic orele de studiu (Study_Hours), calitatea somnului (Sleep_Hours) și frecvența la cursuri (Classes_Attended) împreună performanța academică?"
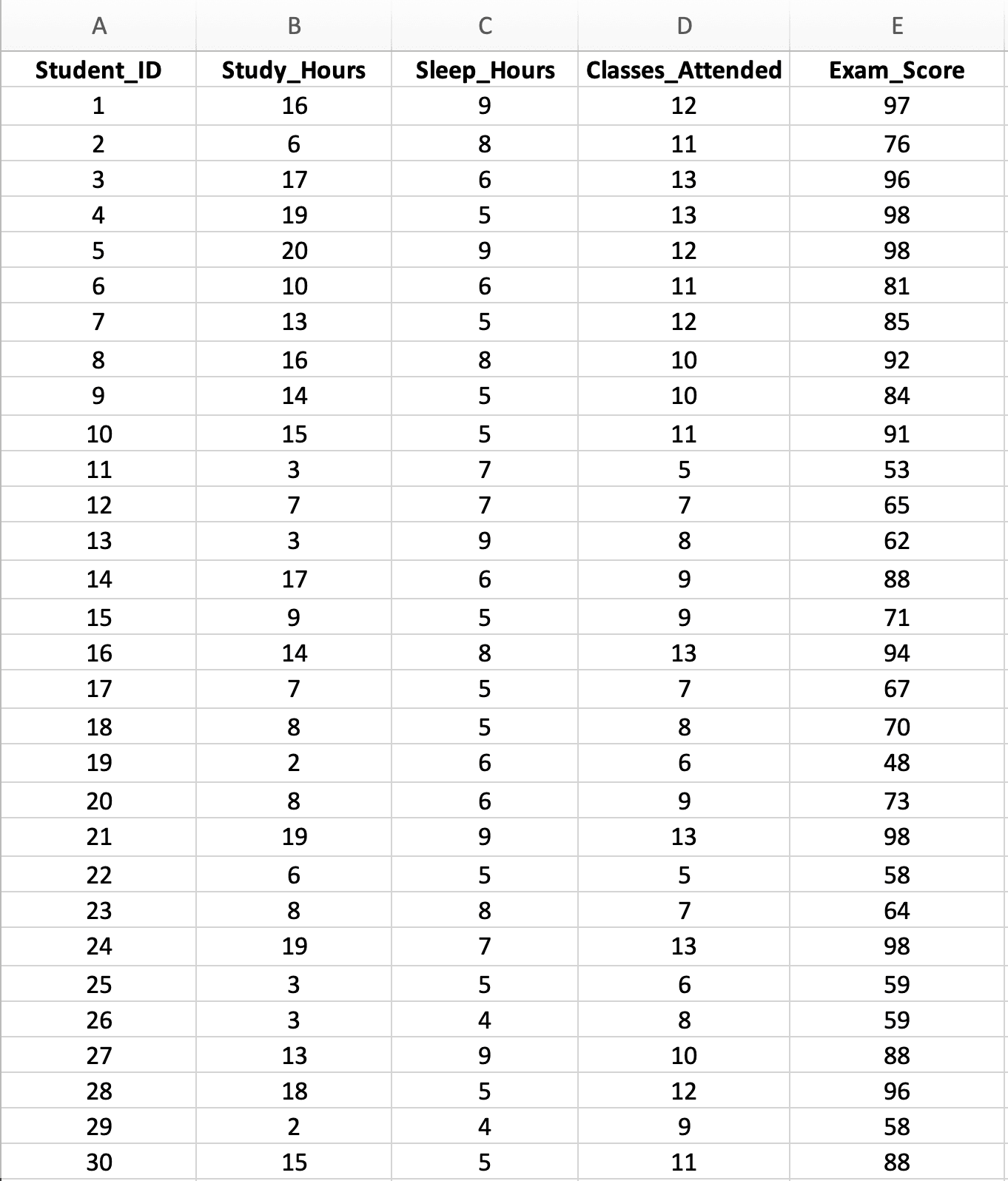
Figura 2: Set de date eșantion cu 30 de studenți arătând trei variabile predictor (Study_Hours, Sleep_Hours, Classes_Attended) și o variabilă rezultat (Exam_Score)
Caracteristicile setului de date:
- Dimensiunea eșantionului: n = 30 studenți (minim pentru 3 predictori, dar adecvat pentru învățare)
- Variabile independente (X):
- X₁: Ore de studiu pe săptămână (Study_Hours) (interval: 2-20 ore)
- X₂: Ore de somn pe noapte (Sleep_Hours) (interval: 4-9 ore)
- X₃: Cursuri frecventate din 15 (Classes_Attended) (interval: 5-15 cursuri)
- Variabilă dependentă (Y): Scor la examen (Exam_Score) (interval: 45-98 puncte)
- Întrebarea de cercetare: Prezic orele de studiu, somnul și frecvența împreună performanța la examen, și care predictor contează cel mai mult?
Creează-ți propriul set de date:
- Introdu datele tale în coloane (toate variabilele X + variabila Y)
- Include anteturi în rândul 1
- Minim n = 50 + 8k observații recomandate (k = numărul de predictori)
- Asigură-te că toate variabilele sunt continue (fără variabile categoriale în regresia multiplă standard)
- Verifică pentru valori lipsă înainte de analiză. Dacă ai cazuri incomplete, vezi cum să gestionezi datele lipsă în Excel înainte de a rula regresia.
Notă despre Dimensiunea Eșantionului: Acest set de date didactic folosește n = 30 în scopuri demonstrative. Pentru cercetarea reală de licență cu 3 predictori, ar trebui să ai cel puțin n = 74 (folosind formula n ≥ 50 + 8k). Exemplul arată relații puternice pentru claritate - datele reale din științele comportamentale arată de obicei efecte mai slabe.
Cum să Calculezi Regresia Liniară Multiplă în Excel (Pas cu Pas)
Analysis ToolPak oferă rezultate cuprinzătoare pentru regresia multiplă incluzând R², R² ajustat, statistica F, semnificația predictorilor individuali și reziduurile. Aceasta este metoda recomandată pentru cercetarea de licență.
Prezentare Generală a Fluxului de Lucru pentru Analiză
Înainte de a rula regresia multiplă, urmează această secvență:
- Verifică multicolinearitatea între predictori (matricea de corelație, r < 0.80)
- Rulează regresia folosind Analysis ToolPak
- Evaluează modelul general (semnificația testului F, R² ajustat)
- Evaluează predictorii individuali (valorile p pentru fiecare coeficient)
- Verifică asumpțiile (grafice de reziduuri pentru normalitate, homoscedasticitate)
- Raportează în format APA (potrivirea modelului, apoi predictorii individuali)
Această secvență asigură identificarea problemelor de multicolinearitate înainte de a investi timp în interpretarea coeficienților care pot fi instabili sau înșelători.
Notă privind Setările Regionale: Formulele Excel folosesc separatori de argumente diferiți în funcție de localizare. Excel US/UK folosește virgule:
=STDEV.S(A1:A30)în timp ce Excel European folosește punct și virgulă:=STDEV.S(A1:A30). Dacă o formulă returnează eroare, încearcă să schimbi virgulele cu punct și virgulă (sau invers). Pentru a verifica sau modifica setările:
- Windows: File → Options → Advanced → "Use system separators"
- Mac: System Preferences → Language & Region → Advanced → Number separators
Pasul 1: Verifică dacă Analysis ToolPak este Activat
Dacă nu ai folosit Analysis ToolPak înainte, activează-l mai întâi:
- Click pe File → Options
- Selectează Add-ins (bara laterală stângă)
- În partea de jos, selectează Excel Add-ins din dropdown-ul "Manage"
- Click pe Go
- Bifează Analysis ToolPak și click pe OK
Ai nevoie de instrucțiuni detaliate? Vezi ghidul nostru complet: Cum să Activezi Data Analysis în Excel
Pasul 2: Accesează Data Analysis și Selectează Regression
Figura 3: Accesarea Data Analysis din tab-ul Data și selectarea Regression
- Click pe tab-ul Data în panglica Excel
- Click pe Data Analysis (partea dreaptă)
- Derulează în jos și selectează Regression
- Click pe OK
Pasul 3: Configurează Dialogul de Regresie pentru Predictori Multipli
Aici regresia multiplă diferă de regresia simplă - vei selecta coloane multiple pentru Input X Range.
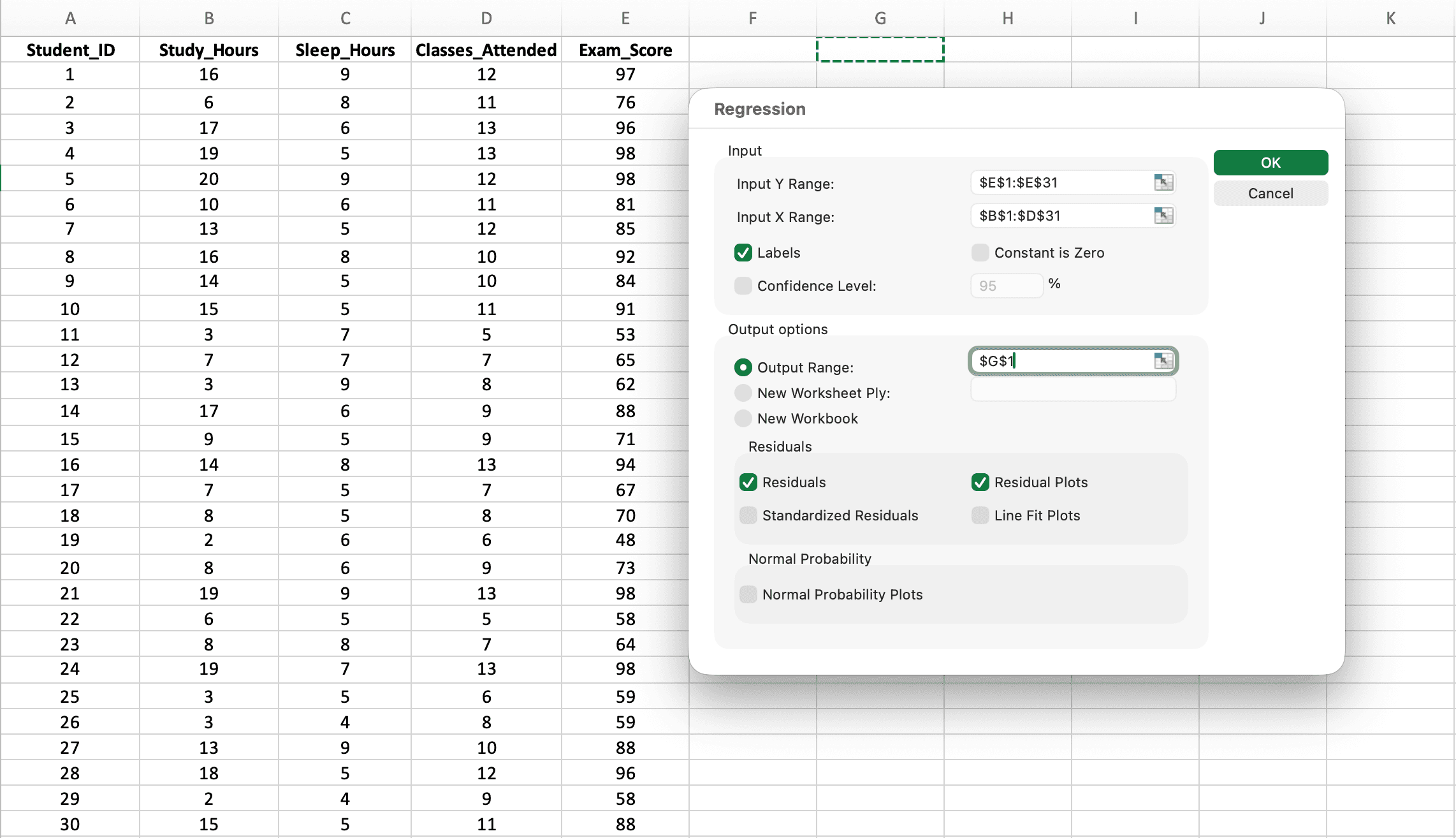
Figura 4: Dialogul de regresie configurat pentru predictori multipli - observă că Input X Range se întinde pe trei coloane (B1:D31)
Setări critice:
-
Input Y Range: Selectează coloana variabilei tale dependente inclusiv antetul (ex.,
E1:E31pentru Exam_Score) -
Input X Range: Selectează TOATE coloanele de predictori împreună inclusiv anteturile (ex.,
B1:D31pentru Study_Hours, Sleep_Hours ȘI Classes_Attended)- Important: Selectează toate coloanele X ca un singur interval continuu, nu separat
- Coloanele trebuie să fie adiacente (una lângă alta)
-
Labels: Bifează această casetă (spune Excel-ului că rândul 1 conține numele variabilelor)
-
Output Range: Click pe o celulă unde ar trebui să apară rezultatele (ex.,
G1) -
Residuals: Bifează aceasta pentru verificarea asumpțiilor
-
Click pe OK
Notă despre Setările Regionale: Excel folosește separatori zecimali diferiți în funcție de localizarea ta. Excel US/UK afișează numerele ca
2.15în timp ce Excel European afișează2,15. Rezultatele regresiei tale vor folosi formatul regional al sistemului tău. Ambele sunt corecte - fii consistent când raportezi rezultatele. Capturile de ecran din acest ghid folosesc formatul european (virgulă ca separator zecimal).
Pasul 4: Înțelegerea Rezultatelor Regresiei Multiple
Excel generează rezultate cuprinzătoare organizate în trei secțiuni principale. Să interpretăm fiecare parte:
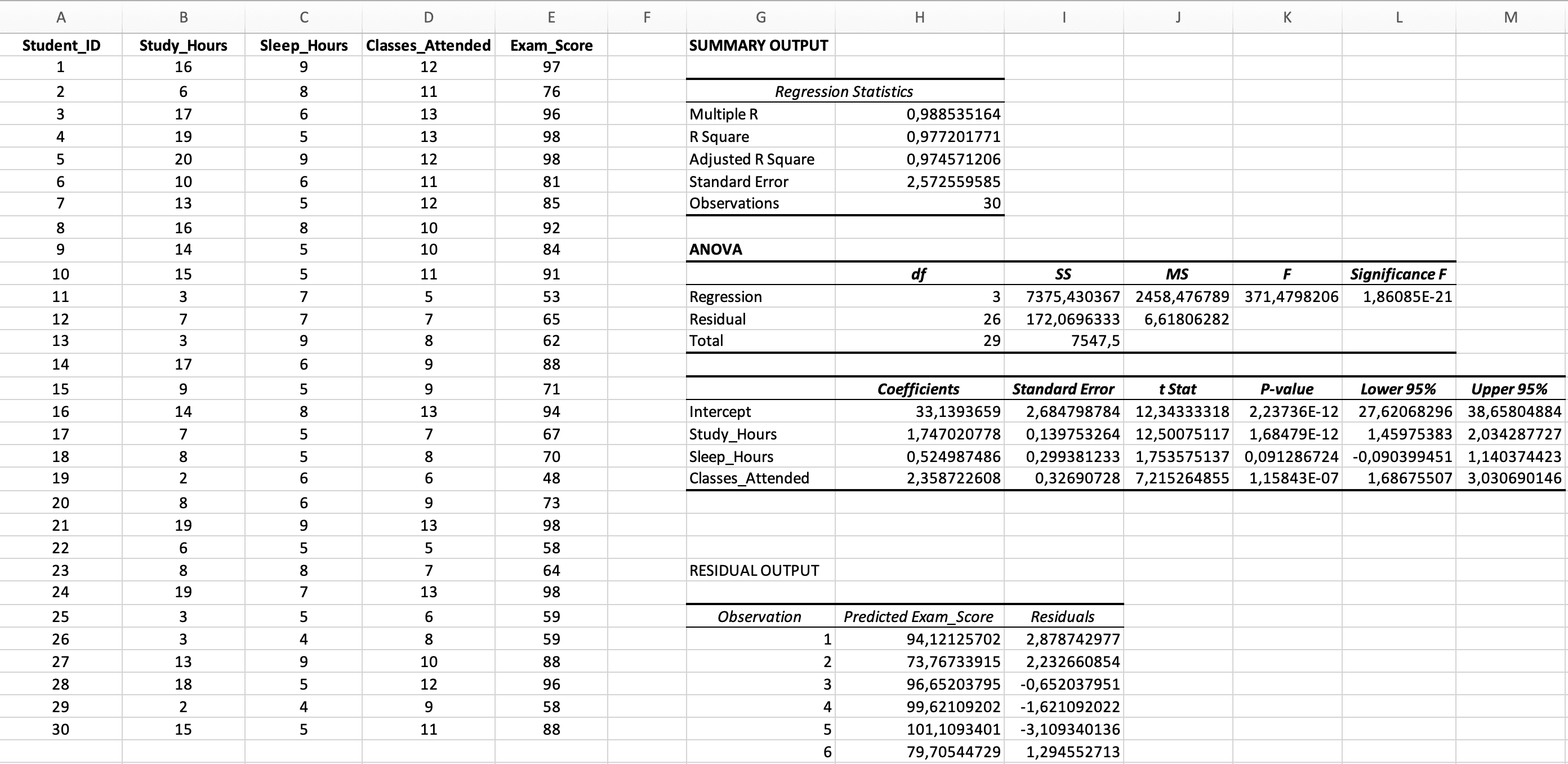
Figura 5: Rezultat complet al regresiei multiple cu secțiunile Regression Statistics, ANOVA și Coefficients
Interpretarea Rezultatelor Regresiei Multiple
Înțelegerea a ce înseamnă fiecare statistică este critică pentru capitolul tău de Rezultate. Rezultatele regresiei multiple necesită interpretare mai atentă decât regresia simplă pentru că evaluezi atât modelul general CÂT ȘI predictorii individuali.
Secțiunea 1: Statistici de Regresie
| Statistică | Valoare Exemplu | Interpretare |
|---|---|---|
| Multiple R | 0.988 | Corelația dintre Y observat și Y prezis (întotdeauna pozitivă) |
| R Square | 0.977 | 97.7% din varianța în scorurile la examen este explicată de cei trei predictori combinați |
| Adjusted R Square | 0.975 | 97.5% ajustat pentru numărul de predictori - folosește acesta pentru regresia multiplă |
| Standard Error | 2.57 | Eroarea medie de predicție (în puncte de scor la examen) |
| Observations | 30 | Dimensiunea eșantionului |
Tabel 2: Interpretarea Rezultatelor Statisticilor de Regresie
De Ce Contează R² Ajustat pentru Regresia Multiplă
Acest lucru este crucial: În regresia multiplă, raportează întotdeauna R² ajustat, nu doar R².
Problema cu R² obișnuit: De fiecare dată când adaugi un predictor la modelul tău, R² crește - chiar dacă acel predictor este inutil (cum ar fi mărimea pantofului prezicând scorurile la examen). R² nu poate niciodată să scadă când adaugi variabile.
Soluția - R² ajustat: Această statistică penalizează adăugarea predictorilor nefolositori. Poate de fapt să scadă dacă o nouă variabilă nu îmbunătățește predicția suficient pentru a justifica includerea ei.
Când să folosești care:
- Regresia simplă (1 predictor): R² și R² ajustat sunt aproape identice - folosește oricare
- Regresia multiplă (2+ predictori): Folosește întotdeauna R² ajustat pentru evaluarea modelului
- Compararea modelelor: Dacă R² ajustat scade când adaugi o variabilă, acea variabilă probabil nu este utilă
Interpretarea magnitudinii R²: Cohen (1988) a sugerat că în cercetarea comportamentală, R² = .02 reprezintă un efect mic, R² = .13 un efect mediu, și R² = .26 un efect mare. Un R² ajustat de .975 în exemplul nostru este excepțional de mare, deși acest set de date didactic a fost proiectat pentru claritate. Cercetarea comportamentală reală produce de obicei efecte mai mici (R² = .10 până la .30 este comun).
Interpretare exemplu: "Modelul cu trei predictori a explicat 97.7% din varianța în scorurile la examen (R² = .977, R² ajustat = .975). Diferența minimă dintre R² și R² ajustat sugerează că toți predictorii contribuie semnificativ la model."
Secțiunea 2: Tabelul ANOVA (Semnificația Modelului General)
| Sursă | df | SS | MS | F | Significance F |
|---|---|---|---|---|---|
| Regression | 3 | 2,638.68 | 879.56 | 373.65 | < 0.001 |
| Residual | 26 | 172.07 | 6.62 | - | - |
| Total | 29 | 2,810.75 | - | - | - |
Tabel 3: Tabelul ANOVA pentru Modelul de Regresie Multiplă
Valoare cheie: Significance F < 0.001
Aceasta testează ipoteza nulă că TOȚI coeficienții de regresie sunt egali cu zero (adică, niciunul dintre predictori nu contează).
- Dacă Significance F < 0.05: Modelul general este semnificativ statistic - cel puțin un predictor este util
- Dacă Significance F ≥ 0.05: Modelul nu este semnificativ - predictorii nu prezic Y
Important: Un model general semnificativ nu înseamnă că TOȚI predictorii sunt semnificativi. Trebuie să verifici fiecare predictor individual în tabelul de Coeficienți.
Interpretare exemplu: "Modelul de regresie a fost semnificativ statistic, F(3, 26) = 373.65, p < .001, indicând că setul de predictori (orele de studiu, somnul și frecvența la cursuri) a prezis semnificativ scorurile la examen."
Secțiunea 3: Tabelul de Coeficienți (Semnificația Predictorilor Individuali)
Aici determini care predictori specifici contează - cea mai importantă parte a rezultatelor regresiei multiple.
| Variabilă | Coefficients (B) | Standard Error | t Stat | P-value | Lower 95% | Upper 95% |
|---|---|---|---|---|---|---|
| Intercept | 33.14 | 2.68 | 12.34 | < 0.001 | 27.63 | 38.65 |
| Study_Hours | 1.75 | 0.14 | 12.50 | < 0.001 | 1.46 | 2.04 |
| Sleep_Hours | 0.52 | 0.30 | 1.75 | 0.092 | -0.09 | 1.14 |
| Classes_Attended | 2.36 | 0.33 | 7.22 | < 0.001 | 1.69 | 3.04 |
Tabel 4: Coeficienții de Regresie cu Semnificația Predictorilor Individuali
Ecuația de regresie:
Care Predictori Sunt Semnificativi? (Interpretare Critică)
Aici mulți studenți fac greșeli. Trebuie să evaluezi valoarea p a fiecărui predictor individual:

Figura 6: Identificarea predictorilor semnificativi vs. nesemnificativi în tabelul de Coeficienți
Interpretarea Fiecărui Predictor
Study_Hours (p < 0.001) - SEMNIFICATIV ✓
- B = 1.75: Pentru fiecare oră suplimentară de studiu pe săptămână, scorurile la examen cresc cu 1.75 puncte, menținând somnul și frecvența constante
- IC 95% [1.46, 2.04]: Efectul adevărat este între 1.46 și 2.04 puncte pe oră
- Concluzie: Orele de studiu sunt un predictor unic semnificativ al scorurilor la examen
Sleep_Hours (p = 0.092) - NESEMNIFICATIV ✗
- B = 0.52: Coeficientul sugerează 0.52 puncte pe oră de somn, DAR...
- p = 0.092 > 0.05: Acest efect nu este semnificativ statistic
- IC 95% [-0.09, 1.14]: Intervalul include zero, confirmând nesemnificația
- Concluzie: Orele de somn nu prezic semnificativ scorurile la examen după controlarea pentru orele de studiu și frecvență
Classes_Attended (p < 0.001) - SEMNIFICATIV ✓
Frecvența la cursuri a apărut și ca predictor semnificativ (B = 2.36, IC 95% [1.69, 3.04]). Fiecare curs suplimentar frecventat corespunde unei creșteri de 2.36 puncte în scorurile la examen când orele de studiu și somnul sunt menținute constante. Intervalul de încredere exclude zero, confirmând că efectul este fiabil statistic.
Ce Înseamnă "Nesemnificativ"?
Când un predictor nu este semnificativ (p ≥ 0.05), înseamnă UNA dintre acestea:
-
Variabila nu prezice de fapt Y - Somnul nu afectează cu adevărat scorurile la examen în această populație
-
Multicolinearitate - Somnul ar putea fi corelat cu orele de studiu, deci când controlăm pentru orele de studiu, somnul nu mai are nicio contribuție unică de explicat
-
Putere insuficientă - Cu un eșantion mai mare, efectul ar putea deveni semnificativ (dimensiunea eșantionului a fost doar n = 30)
-
Efect adevărat dar mic - Efectul există dar este prea mic pentru a fi detectat cu acest eșantion
Cum să raportezi predictorii nesemnificativi: Nu-i ascunde! Raportează toți predictorii pe care i-ai testat, inclusiv pe cei nesemnificativi. Aceasta este onest metodologic și ajută cititorii să înțeleagă modelul tău complet.
Compararea Importanței Predictorilor
O întrebare naturală: "Care predictor contează cel mai mult?" Aceasta necesită coeficienți standardizați.
Coeficienți Standardizați vs Nestandardizați
Excel îți dă coeficienți nestandardizați (B) care sunt în unitățile originale ale fiecărei variabile:
- Ore de studiu: 1.75 puncte pe oră
- Cursuri: 2.36 puncte pe curs
Nu poți compara direct 1.75 vs 2.36 pentru că scalele sunt diferite (ore vs cursuri frecventate).
Calcularea Coeficienților Standardizați (β) în Excel
Pentru a compara importanța predictorilor, calculează manual coeficienții standardizați:
Pași:
- Calculează abaterea standard a fiecărui predictor folosind
=STDEV.S(range) - Calculează abaterea standard a lui Y (scorurile la examen)
- Înmulțește fiecare B nestandardizat cu (SD_X / SD_Y)
Calcule exemplu:
-
SD(Study_Hours) = 5.73, SD(Exam_Score) = 9.65
-
β(Study_Hours) = 1.75 × (5.73 / 9.65) = 1.04
-
SD(Classes_Attended) = 2.56
-
β(Classes_Attended) = 2.36 × (2.56 / 9.65) = 0.63
Interpretare: Orele de studiu (β = 1.04) au un efect standardizat mai mare decât frecvența la cursuri (β = 0.63), făcându-le predictorul mai puternic al performanței la examen.
Notă: Pentru cercetarea formală de licență care necesită coeficienți standardizați, SPSS îi oferă automat în coloana "Standardized Coefficients Beta". Dacă calculezi manual în Excel, verifică rezultatele confirmând că predictorii cu corelații mai puternice cu Y au și coeficienți standardizați mai mari. Dacă clasamentele tale nu se potrivesc, verifică calculele de abatere standard.
Detectarea Multicolinearității în Excel
Multicolinearitatea este PROBLEMA critică unică pentru regresia multiplă pe care tutorialele Excel o ignoră adesea. Apare când variabilele tale predictor sunt puternic corelate între ele - și poate distorsiona serios rezultatele tale.
De Ce Este Multicolinearitatea o Problemă
Când predictorii sunt puternic corelați:
- Coeficienții devin instabili - schimbări mici în date cauzează oscilații mari ale coeficienților
- Erorile standard se umflă - făcând predictorii semnificativi să pară nesemnificativi
- Semnele se pot inversa - un predictor care ar trebui să fie pozitiv devine negativ
- Nu poți spune care predictor contează - efectele lor sunt confundate
Exemplu: Dacă orele de studiu și orele de bibliotecă sunt puternic corelate (r = 0.95), modelul nu poate separa efectele lor. Unul ar putea părea semnificativ în timp ce celălalt nu, dar schimbând pe care îl incluzi ar inversa rezultatele.
Cum să Verifici Multicolinearitatea în Excel
Excel nu poate calcula VIF (Variance Inflation Factor), dar POȚI detecta multicolinearitatea folosind o matrice de corelație:
Pasul 1: Creează o Matrice de Corelație

Figura 7: Matricea de corelație a variabilelor predictor - majoritatea corelațiilor sunt scăzute, cu o valoare la limită (r = 0.82)
- Click pe Data → Data Analysis → Correlation
- Input Range: Selectează doar coloanele tale de predictori (variabilele X), nu Y
- Bifează Labels in first row
- Click pe OK
Pasul 2: Interpretează Matricea de Corelație
| Study_Hours | Sleep_Hours | Classes_Attended | |
|---|---|---|---|
| Study_Hours | 1.00 | 0.25 | 0.82 |
| Sleep_Hours | 0.25 | 1.00 | 0.23 |
| Classes_Attended | 0.82 | 0.23 | 1.00 |
Tabel 5: Matricea de Corelație a Variabilelor Predictor
Reguli de decizie:
- r < 0.70: Fără îngrijorare - predictorii sunt suficient de independenți
- 0.70 ≤ r < 0.80: Îngrijorare moderată - monitorizează dar de obicei acceptabil
- r ≥ 0.80: Îngrijorare ridicată - multicolinearitate probabil problematică
- r ≥ 0.90: Îngrijorare severă - consideră eliminarea unui predictor
În exemplul nostru: Majoritatea corelațiilor sunt scăzute (0.23–0.25). Corelația dintre Study_Hours și Classes_Attended (r = 0.82) este la pragul de 0.80 dar acceptabilă pentru acest exemplu didactic. În cercetarea de licență, ai putea considera dacă aceste variabile măsoară constructe suprapuse - studenții care studiază mai mult pot frecventa și mai multe cursuri. În ciuda acestei corelații la limită, coeficienții noștri de regresie rămân interpretabili și ambii predictori sunt semnificativi.
Semne de Avertizare ale Multicolinearității în Rezultate
Chiar și fără o matrice de corelație, fii atent la aceste semnale roșii în rezultatele regresiei tale:
- Erori standard foarte mari pentru coeficienți (relativ la dimensiunea coeficientului)
- Coeficienți cu semne neașteptate (pozitiv ar trebui să fie negativ, sau invers)
- Model general semnificativ dar fără predictori individuali semnificativi
- Coeficienți care se schimbă dramatic când adaugi/elimini un predictor
Ce Să Faci Dacă Ai Multicolinearitate
Dacă corelațiile dintre predictori depășesc 0.80:
- Elimină unul dintre predictorii corelați - Păstrează-l pe cel mai important teoretic
- Combină predictorii corelați - Creează un scor compozit (ex., media orelor de studiu + orele de bibliotecă)
- Folosește Analiza Componentelor Principale - Necesită SPSS sau R
- Centrează variabilele tale - Scade media din fiecare predictor (ajută cu termenii de interacțiune)
- Raportează-o ca o limitare - Dacă nu o poți rezolva, recunoaște-o
Pentru comisiile de licență care cer VIF: Vei avea nevoie de SPSS sau R. VIF > 5 indică probleme; VIF > 10 este sever. Excel nu poate calcula VIF.
Verificarea Asumpțiilor Regresiei Multiple
Regresia multiplă are cinci asumpții - una în plus față de regresia simplă. Încălcarea asumpțiilor poate invalida valorile p și concluziile tale.
Cele Cinci Asumpții
- Linearitate - Relația dintre fiecare X și Y este liniară
- Independență - Observațiile sunt independente unele de altele
- Normalitatea Reziduurilor - Erorile de predicție sunt distribuite normal
- Homoscedasticitate - Reziduurile au varianță constantă
- Fără Multicolinearitate - Predictorii nu sunt puternic corelați (UNICĂ pentru regresia multiplă)
De ce contează asumpțiile: Fiecare încălcare cauzează probleme specifice. Non-linearitatea distorsionează estimările coeficienților (valorile tale B vor fi greșite). Heteroscedasticitatea umflă erorile standard, făcând efectele cu adevărat semnificative să pară nesemnificative. Non-normalitatea reziduurilor afectează acuratețea intervalelor de încredere și valorilor p, în special în eșantioanele mai mici. Multicolinearitatea face coeficienții individuali neinterpretabili pentru că modelul nu poate separa efectele predictorilor corelați.
Asumpția 1: Linearitate
Cum să verifici: Creează diagrame de dispersie ale fiecărui X vs Y individual.
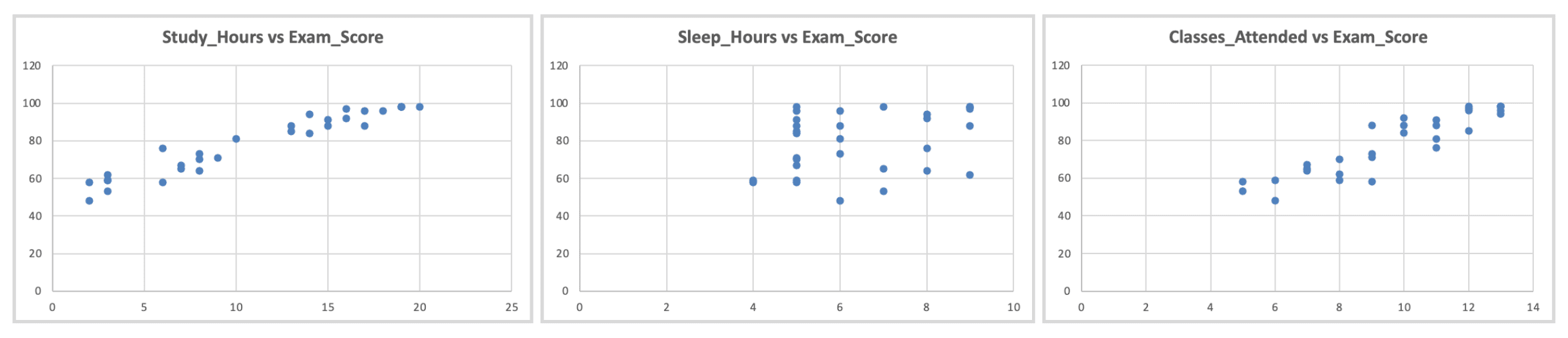
Figura 8: Verificarea linearității - diagrame de dispersie ale fiecărui predictor vs. rezultat arătând relații aproximativ liniare
Ce să cauți: Paternuri aproximativ liniare (nu curbate, în formă de U sau exponențiale)
Asumpția 2: Independență
Aceasta este o problemă de design al cercetării, nu ceva ce testezi statistic.
Independent: Fiecare observație este o persoană diferită, măsurată o singură dată Nu este independent: Aceleași persoane măsurate de mai multe ori, sau persoane grupate în clustere (săli de clasă, familii)
Excel nu poate testa aceasta - asigură independența prin designul cercetării tale.
Asumpția 3: Normalitatea Reziduurilor
Cum să verifici: Creează o histogramă a reziduurilor.
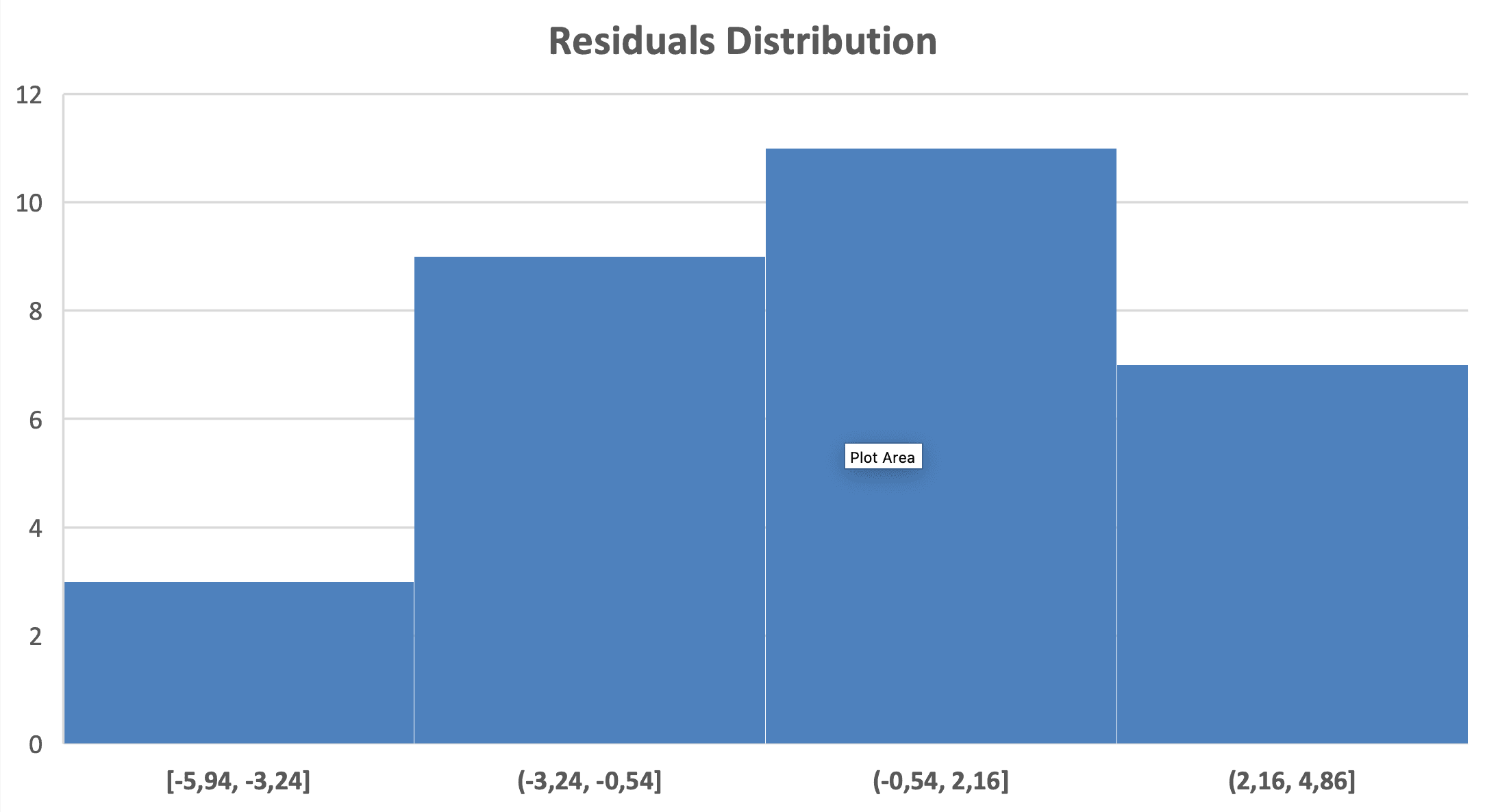
Figura 9: Verificarea normalității - histograma reziduurilor arată distribuție aproximativ normală
Pași:
- Bifează caseta Residuals în dialogul de regresie
- Găsește coloana Residuals în rezultate
- Creează histogramă: Selectează reziduurile → Insert → Histogram (pentru crearea detaliată a histogramei, vezi ghidul nostru de statistică descriptivă)
Ce să cauți: Distribuție în formă de clopot, simetrică, centrată în jurul valorii zero.
Asumpția 4: Homoscedasticitate (Varianță Constantă)
Cum să verifici: Reprezintă grafic reziduurile vs. valorile prezise (fitted).
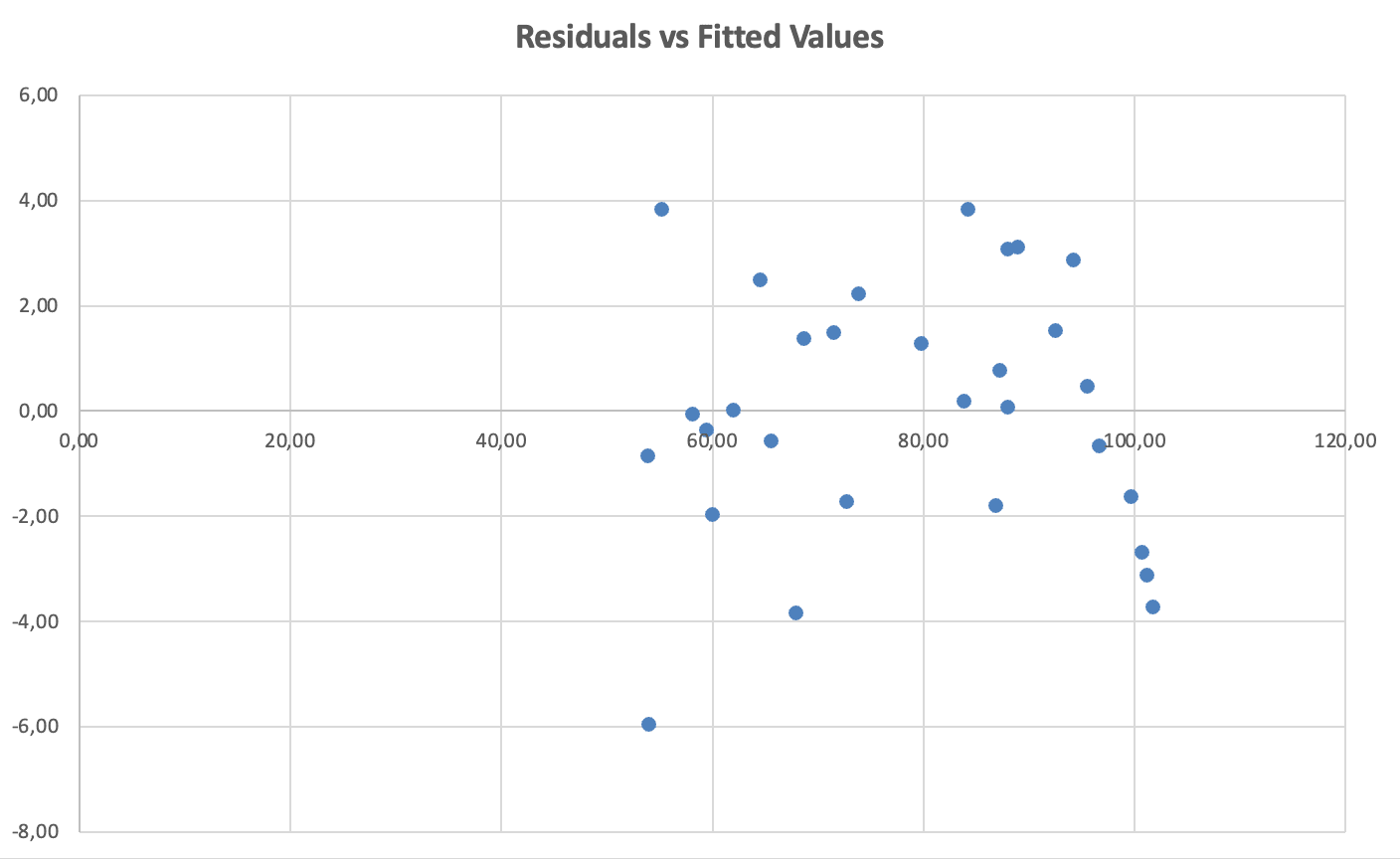
Figura 10: Verificarea homoscedasticității - reziduurile vs. valorile fitted arată dispersie constantă (fără patern de pâlnie)
Ce să cauți: Dispersie aleatorie în jurul valorii zero cu răspândire aproximativ constantă pe toate valorile fitted. Încălcare: Formă de pâlnie sau con (răspândirea crește sau scade).
Asumpția 5: Fără Multicolinearitate (UNICĂ pentru Regresia Multiplă)
Cum să verifici: Matricea de corelație a predictorilor (acoperită în secțiunea anterioară).
Regula: Corelațiile dintre predictori ar trebui să fie sub 0.80.
Raportarea Asumpțiilor în Lucrarea Ta
În secțiunea de Metodologie:
"Înainte de analiză, au fost evaluate asumpțiile pentru regresia liniară multiplă. Diagramele de dispersie au indicat relații liniare între fiecare predictor și variabila rezultat. Statistica Durbin-Watson nu a fost disponibilă în Excel; totuși, observațiile au fost independente prin designul cercetării (studenți diferiți cu măsurători unice). Histogramele reziduurilor au arătat distribuție aproximativ normală, iar graficele de reziduuri au indicat varianță constantă (homoscedasticitate). Multicolinearitatea a fost evaluată folosind o matrice de corelație a variabilelor predictor; majoritatea corelațiilor au fost scăzute (r = 0.23–0.25), deși Study_Hours și Classes_Attended au arătat o corelație la limită (r = 0.82) care a fost monitorizată dar nu a afectat substanțial interpretabilitatea coeficienților."
Cum să Raportezi Regresia Multiplă în Format APA Ediția a 7-a
Comisia ta de licență se așteaptă ca rezultatele regresiei multiple să fie raportate cu elemente specifice. Iată formatul complet.
Șablon pentru Secțiunea de Rezultate APA
Format paragraf:
"S-a efectuat o regresie liniară multiplă pentru a examina dacă orele de studiu, orele de somn și frecvența la cursuri prezic scorurile finale la examen. Analizele preliminare au confirmat că asumpțiile de linearitate, independență, normalitate a reziduurilor, homoscedasticitate și absența multicolinearității au fost îndeplinite.
Modelul de regresie multiplă a prezis semnificativ statistic scorurile la examen, F(3, 26) = 373.65, p < .001, R² = .98, R² ajustat = .97. Cei trei predictori împreună au explicat 97.7% din varianța în scorurile la examen. Coeficienții de regresie sunt prezentați în Tabelul [X].
Orele de studiu au prezis semnificativ scorurile la examen (B = 1.75, IC 95% [1.46, 2.04], p < .001), la fel și frecvența la cursuri (B = 2.36, IC 95% [1.69, 3.04], p < .001). Orele de somn nu au fost un predictor semnificativ statistic (B = 0.52, IC 95% [-0.09, 1.14], p = .092). Pentru fiecare oră suplimentară de studiu săptămânal, scorurile la examen au crescut cu 1.75 puncte, controlând pentru somn și frecvență. Fiecare curs suplimentar frecventat a fost asociat cu o creștere de 2.36 puncte în scorurile la examen, controlând pentru ceilalți predictori."
Format Tabel de Regresie APA
Tabelul [X]
Regresie Liniară Multiplă Prezicând Scorurile la Examen
| Variabilă | B | SE | β | t | p | IC 95% |
|---|---|---|---|---|---|---|
| Intercept | 33.14 | 2.68 | — | 12.34 | < .001 | [27.63, 38.65] |
| Ore de Studiu | 1.75 | 0.14 | 1.04 | 12.50 | < .001 | [1.46, 2.04] |
| Ore de Somn | 0.52 | 0.30 | .09 | 1.75 | .092 | [-0.09, 1.14] |
| Cursuri Frecventate | 2.36 | 0.33 | .63 | 7.22 | < .001 | [1.69, 3.04] |
Tabel 6: Regresie Liniară Multiplă Prezicând Scorurile la Examen din Orele de Studiu, Orele de Somn și Frecvența la Cursuri
Notă. n = 30. R² = .98, R² ajustat = .97, F(3, 26) = 373.65, p < .001. B = coeficient nestandardizat. SE = eroare standard. β = coeficient standardizat. IC = interval de încredere.
Lista de Verificare pentru Raportarea Regresiei Multiple
Include TOATE aceste elemente:
În text (paragraful de Rezultate):
- Tipul analizei ("S-a efectuat o regresie liniară multiplă...")
- Variabilele testate (toți predictorii și rezultatul)
- Declarație despre verificarea asumpțiilor
- Semnificația modelului general: F(df_regresie, df_rezidual) = valoarea F, valoarea p
- R² ȘI R² ajustat cu interpretare
- Pentru FIECARE predictor: valoarea B, IC 95% și valoarea p
- Declarație clară despre care predictori au fost/nu au fost semnificativi
- Interpretarea coeficienților semnificativi cu direcție
În tabel:
- Numărul tabelului și titlul în italice
- Toți predictorii inclusiv interceptul
- B (coeficienți nestandardizați)
- SE (erori standard)
- β (coeficienți standardizați) dacă sunt calculați
- Statisticile t
- Valorile p
- Intervale de încredere 95%
- Nota tabelului cu n, R², R² ajustat, statistica F
Greșeli Comune în Regresia Multiplă
Evită aceste erori frecvente care pot compromite cercetarea ta de licență:
1. Raportarea R² în Loc de R² Ajustat
Greșeala: "Modelul a explicat 97.5% din varianță (R² = .975)"
De ce este greșit: R² crește întotdeauna cu mai mulți predictori, chiar și cu cei inutili. R² ajustat corectează pentru aceasta.
Cum să corectezi: Raportează R² ajustat ca mărime a efectului principal, sau raportează ambele: "R² = .972, R² ajustat = .969"
2. Ignorarea Multicolinearității
Greșeala: Adăugarea predictorilor puternic corelați fără verificare.
De ce este greșit: Coeficienții devin instabili, erorile standard se umflă, și nu poți interpreta care predictor contează.
Cum să corectezi: Creează întotdeauna matricea de corelație a predictorilor înainte de a rula regresia. Elimină sau combină variabilele cu r > 0.80.
3. Eliminarea Predictorilor Nesemnificativi Fără Justificare
Greșeala: "Somnul nu a fost semnificativ, așa că l-am eliminat și am rerulat analiza."
De ce este greșit: Eliminarea variabilelor schimbă semnificația celorlalți coeficienți. Eliminarea selectivă poate duce la rezultate distorsionate.
Cum să corectezi: Păstrează toți predictorii relevanți teoretic. Raportează-i pe cei nesemnificativi ca nesemnificativi. Elimină doar dacă ai motive teoretice puternice ȘI raportează că ai făcut-o.
4. Interpretarea Coeficienților ca "Cei Mai Importanți"
Greșeala: "Orele de studiu (B = 2.15) sunt mai importante decât frecvența (B = 1.85) pentru că 2.15 > 1.85."
De ce este greșit: Coeficienții nestandardizați depind de scara fiecărei variabile. Compari ore cu cursuri - unități diferite.
Cum să corectezi: Calculează și compară coeficienții standardizați (β) pentru comparații de importanță.
5. Afirmarea Cauzalității din Regresie
Greșeala: "Studiatul mai mult CAUZEAZĂ scoruri mai mari la examen."
De ce este greșit: Regresia arată predicție și asociere, nu cauzalitate. Cauzalitatea necesită design experimental cu alocare aleatorie.
Cum să corectezi: Folosește limbaj atent - "a prezis," "asociat cu," "legat de" în loc de "a cauzat," "a dus la," "a rezultat în."
6. Neverificarea Asumpțiilor
Greșeala: Rularea regresiei fără verificarea linearității, normalității, homoscedasticității și multicolinearității.
De ce este greșit: Asumpțiile încălcate duc la coeficienți distorsionați și valori p invalide.
Cum să corectezi: Verifică întotdeauna toate cele cinci asumpții înainte de a finaliza rezultatele. Raportează verificarea asumpțiilor în Metodologie.
7. Folosirea Prea Multor Predictori pentru Dimensiunea Eșantionului
Greșeala: Includerea a 10 predictori cu doar 50 de observații.
De ce este greșit: Overfitting-ul apare când modelul se potrivește eșantionului tău dar nu reușește să generalizeze. Cerința minimă este n ≥ 50 + 8k.
Cum să corectezi: Urmează ghidurile pentru dimensiunea eșantionului. Pentru 10 predictori, ai nevoie de cel puțin n = 130 observații. Dacă datele lipsă au redus eșantionul disponibil, adresează aceasta mai întâi. Vezi cum să gestionezi datele lipsă pentru strategii de maximizare a dimensiunii eșantionului utilizabil.
Ce Nu Poate Face Excel: Limitări pentru Cercetarea de Licență
Analysis ToolPak din Excel gestionează bine regresia liniară multiplă standard, dar are limitări semnificative pentru tehnicile avansate. Înțelegerea acestora te ajută să alegi software-ul potrivit.
Tipuri de Regresie care Necesită SPSS sau R
| Tehnică | Ce Face | Excel? | Folosește În Schimb |
|---|---|---|---|
| Regresie Logistică | Prezice rezultate binare (da/nu) | Nu | SPSS, R |
| Regresie Stepwise | Selecție automată a variabilelor | Nu | SPSS, R |
| Regresie Ierarhică | Adaugă predictori în blocuri | Nu | SPSS |
| Analiză de Moderare | Testează efectele de interacțiune | Nu | SPSS PROCESS |
| Analiză de Mediere | Testează efectele indirecte | Nu | SPSS PROCESS |
| Calcul VIF | Test formal de multicolinearitate | Nu | SPSS, R |
| Durbin-Watson | Testează autocorelația | Nu | SPSS, R |
| Regresie Polinomială | Relații curbe | Da (manual) | SPSS, R |
| Regresie Liniară Multiplă | 2+ predictori continui | Da | Toate software-urile |
Tabel 7: Capabilitățile de Regresie Excel vs. Cerințele Software-ului Statistic
Când să Folosești Excel vs SPSS/R
Folosește Excel când:
- Doar regresie liniară multiplă standard
- Variabilă rezultat continuă
- Nu ai nevoie de VIF (matricea de corelație este suficientă)
- Comisia acceptă rezultatele Excel
- Înveți regresia înainte de metodele avansate
Folosește SPSS/R când:
- Rezultate binare/categoriale (regresie logistică)
- Ai nevoie de regresie stepwise sau ierarhică
- Testezi moderare sau mediere
- Comisia cere VIF, Durbin-Watson
- Publici în jurnale care cer rezultate SPSS/R
Concluzie cheie: Excel este excelent pentru învățarea regresiei multiple și pentru analizele de bază ale licenței. Pentru tehnici avansate sau testarea formală a multicolinearității, vei avea nevoie de SPSS sau R. Verifică cu îndrumătorul cerințele software.
Întrebări Frecvente
Întrebări pe Care Comisia Le Poate Adresa
Comisiile de licență adresează frecvent aceste întrebări despre analizele de regresie multiplă. Pregătirea răspunsurilor în avans demonstrează competență statistică și întărește susținerea ta.
"De ce ai inclus acești predictori specifici?"
Fii pregătit să justifici fiecare variabilă pe baza teoriei și cercetărilor anterioare, nu doar convenienței statistice. Citează literatura care arată de ce fiecare predictor ar trebui să fie logic legat de rezultatul tău. Comisiile sunt sceptice față de "data dredging" unde predictorii au fost incluși doar pentru că datele erau disponibile.
"Ai verificat multicolinearitatea?"
Arată matricea ta de corelație și explică că toate corelațiile dintre predictori au fost sub 0.80 (sau orice prag ai folosit). Dacă ești întrebat despre VIF și ai folosit Excel, explică că deși Excel nu poate calcula VIF direct, metoda matricei de corelație identifică multicolinearitatea problematică. Recunoaște că SPSS sau R ar fi necesare pentru testarea formală VIF.
"De ce nu este [variabila] semnificativă?"
Un predictor nesemnificativ nu înseamnă că variabila este neimportantă. Explică că atunci când controlezi pentru ceilalți predictori, contribuția unică a acestei variabile nu a fost statistic diferită de zero. Motive posibile includ: suprapunere cu alți predictori (varianță partajată), dimensiune insuficientă a eșantionului pentru a detecta un efect mic, sau genuină lipsă a unei relații unice după controlarea pentru confunderi.
"Care este semnificația practică a acestor rezultate?"
Semnificația statistică nu este același lucru cu importanța practică. Fii pregătit să explici ce înseamnă un coeficient în termeni reali. De exemplu: "Fiecare oră suplimentară de studiu este asociată cu o creștere de 1.75 puncte în scorurile la examen. Pe parcursul unui semestru, un student care studiază 10 ore mai mult pe săptămână decât media ar putea aștepta aproximativ 17.5 puncte suplimentare, potențial diferența dintre un B și un A."
"De ce nu ai folosit SPSS sau R?"
Dacă ești întrebat, explică că Analysis ToolPak din Excel gestionează adecvat regresia liniară multiplă standard pentru designul tău de cercetare. Recunoaște limitările Excel (fără VIF, fără regresie stepwise, fără regresie logistică) și explică de ce acestea nu au fost necesare pentru analiza ta specifică. Dacă comisia ta preferă puternic rezultate SPSS, oferă-te să replici analiza în SPSS pentru depunerea finală.
Pașii Următori: Aplicarea Regresiei Multiple la Lucrarea Ta
Acum ai un cadru complet pentru efectuarea regresiei liniare multiple în Excel - de la înțelegerea când să o folosești, prin rularea analizei, până la interpretarea rezultatelor și raportarea în format APA. Cheia succesului nu este doar rularea analizei, ci înțelegerea a ce înseamnă fiecare rezultat și verificarea că datele tale îndeplinesc asumpțiile.
Înainte de a finaliza analiza:
-
Verifică multicolinearitatea mai întâi - Creează o matrice de corelație a predictorilor înainte de a rula regresia. Corelațiile > 0.80 necesită acțiune.
-
Verifică toate cele cinci asumpții - Linearitate, independență, normalitatea reziduurilor, homoscedasticitate ȘI fără multicolinearitate.
-
Folosește R² ajustat - Aceasta este mărimea efectului potrivită pentru regresia multiplă, nu R² obișnuit.
-
Raportează TOȚI predictorii - Include predictorii nesemnificativi în tabelul de Rezultate. Nu elimina selectiv variabile fără justificare puternică.
-
Cunoaște limitările Excel - Dacă ai nevoie de VIF, regresie stepwise sau regresie logistică, vei avea nevoie de SPSS sau R.
Ghiduri conexe pentru a continua învățarea:
- Cerință prealabilă: Regresia Liniară Simplă în Excel - Revizuiește dacă conceptele de aici nu au fost clare
- Corelație: Coeficientul de Corelație Pearson - Pentru verificarea multicolinearității
- Mărimea Efectului: Cum să Calculezi Mărimea Efectului - Pentru interpretarea semnificației practice
- Raportare: Raportează Statistica Descriptivă în APA - Pentru capitole complete de Rezultate
- Diferențe între Grupuri: ANOVA în Excel - Când predictorii sunt grupuri categoriale
Referințe
American Psychological Association. (2020). Publication manual of the American Psychological Association (7th ed.). https://doi.org/10.1037/0000165-000
Cohen, J. (1988). Statistical power analysis for the behavioral sciences (2nd ed.). Lawrence Erlbaum Associates.
Green, S. B. (1991). How many subjects does it take to do a regression analysis? Multivariate Behavioral Research, 26(3), 499–510. https://doi.org/10.1207/s15327906mbr2603_7
Hair, J. F., Black, W. C., Babin, B. J., & Anderson, R. E. (2019). Multivariate data analysis (8th ed.). Cengage Learning.
Tabachnick, B. G., & Fidell, L. S. (2019). Using multivariate statistics (7th ed.). Pearson.
