ANOVA cu un factor (analiza varianței) este un test statistic care compară mediile a trei sau mai multe grupuri independente pentru a determina dacă cel puțin o medie de grup diferă semnificativ de celelalte. Deși Excel nu este la fel de puternic ca SPSS sau R pentru statistici avansate, gestionează competent ANOVA cu un factor prin Data Analysis ToolPak.
Acest tutorial complet îți arată cum să calculezi ANOVA cu un factor în Excel pas cu pas, incluzând testarea asumpțiilor, calculul mărimii efectului și format de raportare APA pentru teza sau disertația ta.
Ce este ANOVA cu Un Factor?
ANOVA cu un factor testează dacă mediile a trei sau mai multe grupuri independente diferă pe o variabilă dependentă continuă. „Un factor" se referă la faptul că ai o variabilă independentă (factor) cu multiple nivele (grupuri).
Exemplu de întrebare de cercetare: „Scorurile de satisfacție ale clienților diferă între cele trei grupe de vârstă (18-25, 26-40, 41+)?"
- Variabila Independentă (Factor): Grupa de vârstă (3 nivele)
- Variabila Dependentă: Scor de satisfacție (continuă)
- Ipoteza Nulă (H₀): Toate mediile grupurilor sunt egale (μ₁ = μ₂ = μ₃)
- Ipoteza Alternativă (H₁): Cel puțin o medie de grup diferă
Când să Folosești ANOVA vs Test T
Folosește ANOVA cu un factor când compari trei sau mai multe grupuri. Nu efectua niciodată teste t multiple pentru a compara multiple grupuri. Aceasta îți mărește rata de eroare de Tipul I.
Pentru un ghid complet de decizie, vezi: Test T vs ANOVA în Excel: Care Să Folosești?
Regulă rapidă de decizie:
- 2 grupuri → Folosește test t pentru eșantioane independente
- 3+ grupuri → Folosește ANOVA cu un factor
Cerințe Prealabile: Activează Data Analysis ToolPak
Înainte de a efectua ANOVA, trebuie să activezi add-in-ul Analysis ToolPak din Excel.
Pentru instrucțiuni detaliate de instalare atât pentru Windows cât și pentru Mac, vezi ghidul nostru complet: Cum să Activezi Analiza de Date în Excel
Pași rapizi pentru Windows:
- Click pe Fișier → Opțiuni
- Selectează Programe de completare din meniul din stânga
- În caseta Gestionare de jos, selectează Programe de completare Excel și click pe Salt la
- Bifează caseta Analysis ToolPak
- Click pe OK
Butonul Analiză de date va apărea acum în tab-ul Date sub grupul Analiză.
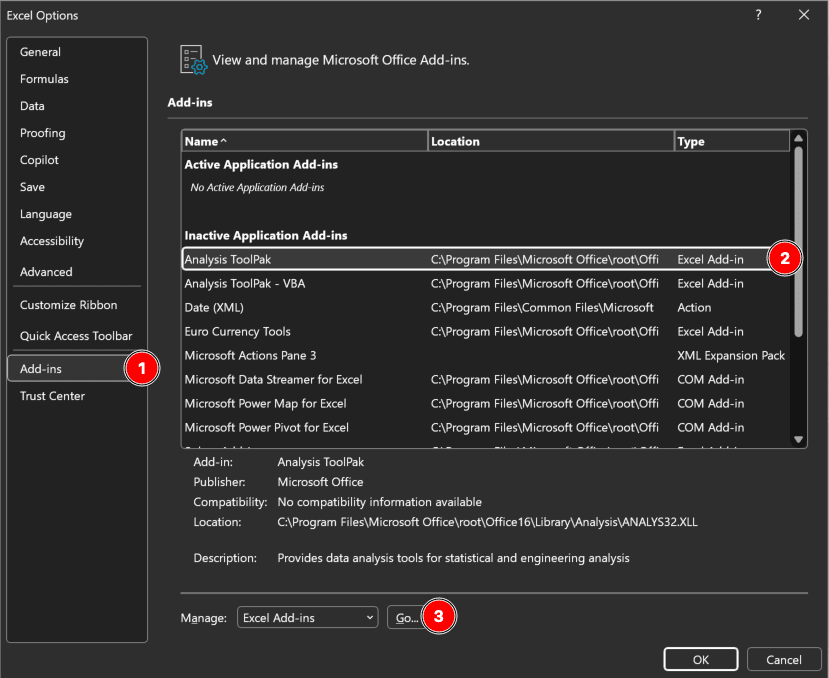 Figura 1: Caseta de dialog Programe de completare Excel cu Analysis ToolPak activat (Windows)
Figura 1: Caseta de dialog Programe de completare Excel cu Analysis ToolPak activat (Windows)
Utilizatori Mac: Mergi la Instrumente → Programe de completare Excel în loc de Fișier → Opțiuni.
Pas cu Pas: Cum să Calculezi ANOVA cu Un Factor în Excel
Vom folosi un set de date exemplu care compară scorurile de satisfacție ale clienților între trei grupe de vârstă.
Pasul 1: Organizează Datele
Aranjează datele în coloane, cu fiecare coloană reprezentând un grup. Include un rând de antet cu etichete de grup.
Exemplu de structură a datelor:
| Vârsta 18-25 | Vârsta 26-40 | Vârsta 41+ |
|---|---|---|
| 3,2 | 4,1 | 4,3 |
| 2,8 | 3,9 | 4,5 |
| 3,5 | 4,3 | 4,2 |
| 3,1 | 4,0 | 4,6 |
| 2,9 | 4,2 | 4,4 |
| 3,4 | 3,8 | 4,1 |
| 3,0 | 4,4 | 4,7 |
| 3,3 | 4,1 | 4,3 |
| 2,7 | 3,7 | 4,0 |
| 3,6 | 4,5 | 4,8 |
Tabel 1: Scoruri de satisfacție ale clienților pe grupe de vârstă (scară 1-5)
Puncte cheie:
- Fiecare coloană = un grup (Vârsta 18-25, Vârsta 26-40, Vârsta 41+)
- Fiecare rând = un respondent
- Etichetele grupurilor sunt în Rândul 1
- Datele numerice încep de la Rândul 2
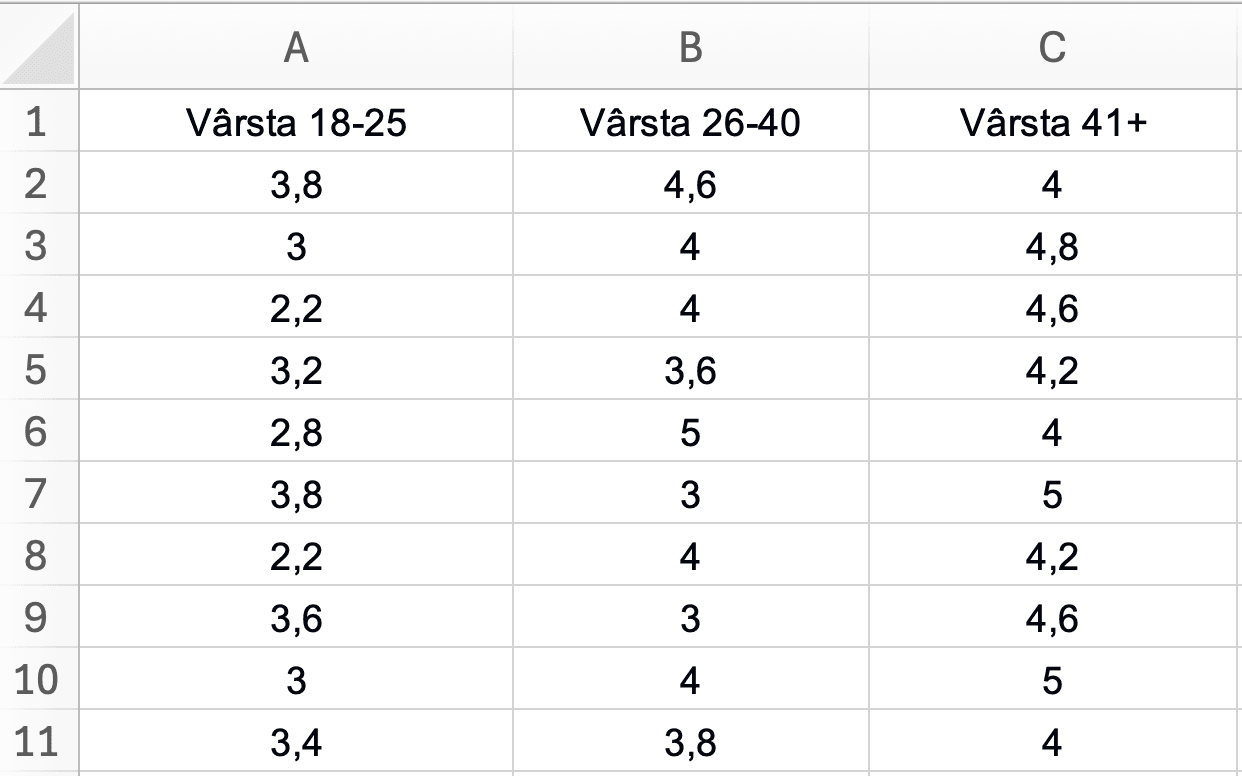 Figura 2: Aranjarea corectă a datelor pentru ANOVA cu un factor - fiecare grupă de vârstă într-o coloană separată cu antete descriptive
Figura 2: Aranjarea corectă a datelor pentru ANOVA cu un factor - fiecare grupă de vârstă într-o coloană separată cu antete descriptive
Pasul 2: Accesează Analiză de Date
- Click pe tab-ul Date
- În grupul Analiză (partea dreaptă), click pe Analiză de date
- Va apărea o casetă de dialog cu instrumente de analiză
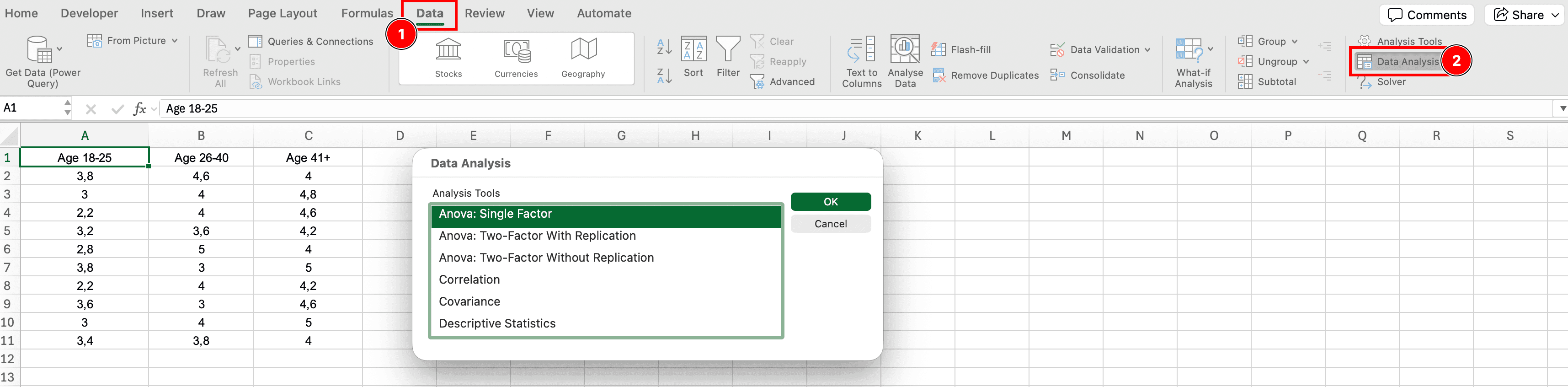 Figura 3: Locația butonului Analiză de date în tab-ul Date din Excel
Figura 3: Locația butonului Analiză de date în tab-ul Date din Excel
Pasul 3: Selectează Anova: Factor Unic
- În caseta de dialog Analiză de date, derulează în jos și selectează Anova: Factor unic
- Click pe OK
„Factor unic" înseamnă o variabilă independentă (grupa de vârstă). Pentru două variabile independente, ai folosi „Anova: Doi factori."
Pasul 4: Configurează Setările ANOVA
Apare caseta de dialog Anova: Factor unic. Configurează aceste setări:
Interval de intrare:
- Click pe pictograma de selector de interval
- Selectează toate datele incluzând antetele (ex: A1:C11)
- Asigură-te că incluzi atât etichetele cât și valorile
Grupat după:
- Selectează Coloane (datele sunt organizate în coloane)
Etichete în primul rând:
- Bifează această casetă (pentru că Rândul 1 conține antete de grup)
Alpha:
- Lasă la 0.05 (nivel de semnificație standard de 95%)
Opțiuni de ieșire:
- Selectează Interval de ieșire și click pe o celulă (ex: E1)
- SAU selectează Foaie nouă pentru a crea o foaie separată
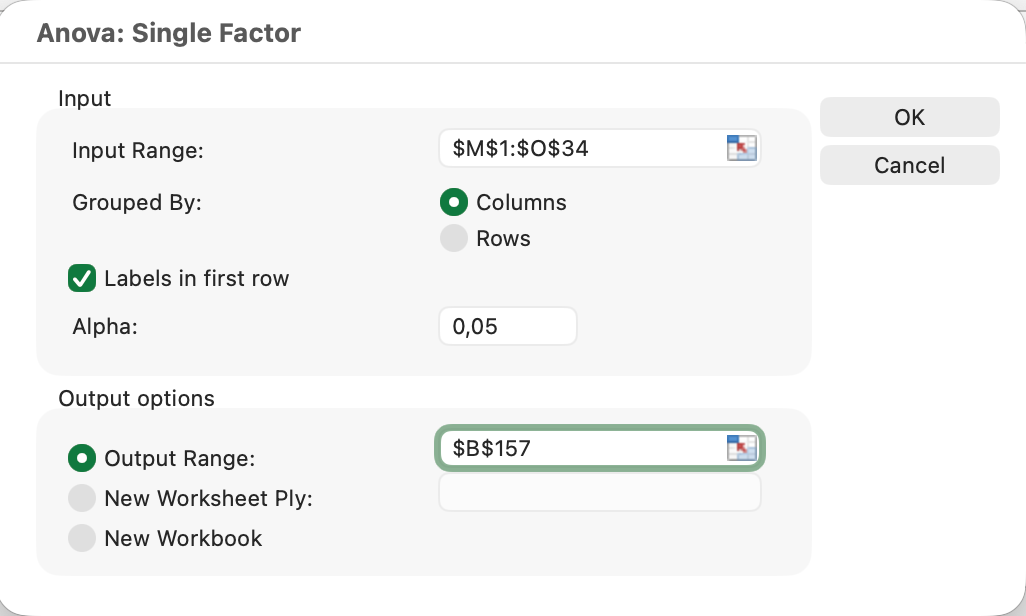 Figura 4: Configurarea casetei de dialog Anova: Factor unic cu trei grupe de vârstă
Figura 4: Configurarea casetei de dialog Anova: Factor unic cu trei grupe de vârstă
Click pe OK pentru a genera rezultatele.
Pasul 5: Interpretează Rezultatele ANOVA
Excel generează două tabele:
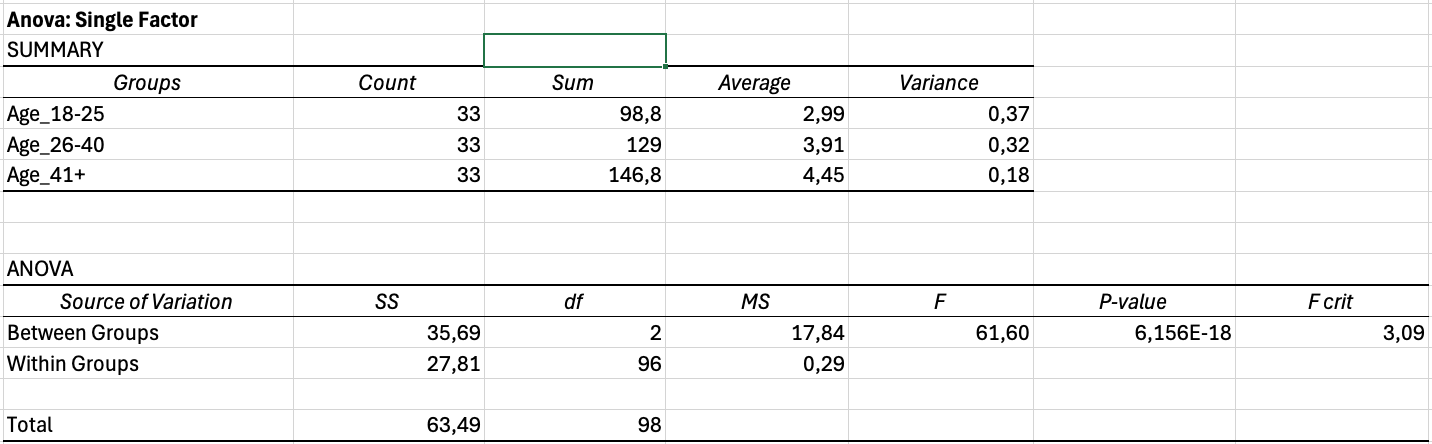 Figura 5: Ieșirea ANOVA din Excel cu statistici descriptive și testul F
Figura 5: Ieșirea ANOVA din Excel cu statistici descriptive și testul F
Tabel 1: Rezumat (Statistici Descriptive)
Acest tabel arată pentru fiecare grup:
- Număr = Dimensiunea eșantionului (câte observații)
- Sumă = Suma tuturor valorilor
- Medie = Media grupului
- Varianță = Varianța grupului
Exemplu de interpretare:
- Grupa vârstă 18-25: M = 3.2, n = 30
- Grupa vârstă 26-40: M = 4.1, n = 30
- Grupa vârstă 41+: M = 4.3, n = 30
Tabel 2: ANOVA (Testul Principal)
Acesta este tabelul crucial pentru testarea ipotezelor:
| Sursa Variației | SS | df | MS | F | Valoare P | F critic |
|---|---|---|---|---|---|---|
| Între grupuri | 31,44 | 2 | 15,72 | 61,60 | 0,001 | 3,10 |
| În interiorul grupurilor | 22,23 | 87 | 0,26 | — | — | — |
| Total | 53,67 | 89 | — | — | — | — |
Tabel 2: Tabel ANOVA arătând diferențe semnificative între grupuri (p < 0.001)
Explicația coloanelor:
- SS (Suma pătratelor): Variația totală împărțită în „Între grupuri" (diferențe între mediile grupurilor) și „În interiorul grupurilor" (diferențe în interiorul fiecărui grup)
- df (Grade de libertate): Între grupuri = k - 1 (3 grupuri - 1 = 2); În interiorul grupurilor = N - k (90 - 3 = 87)
- MS (Pătratul mediu): SS împărțit la df
- F: Statistica testului = MS Între grupuri / MS În interiorul grupurilor
- Valoare P: Probabilitatea de a obține acest rezultat dacă ipoteza nulă este adevărată
- F critic: Valoarea tabelară F pentru alpha = 0.05
Interpretarea dvs.:
Dacă Valoarea P < 0.05: Respinge ipoteza nulă. Cel puțin o medie de grup diferă semnificativ.
Dacă Valoarea P ≥ 0.05: Nu respinge ipoteza nulă. Nu există diferențe semnificative între grupuri.
Exemplu: F(2, 87) = 61.60, p < 0.001
Aceasta înseamnă că există diferențe extrem de semnificative în satisfacție între grupele de vârstă.
Verificarea Asumpțiilor ANOVA
ANOVA are trei asumpții principale care trebuie îndeplinite:
1. Independența Observațiilor
Ce înseamnă: Fiecare observație trebuie să fie independentă. Scorul unei persoane nu ar trebui să influențeze scorul altei persoane.
Cum să verifici: Verifică design-ul cercetării:
- Fiecare participant apare o singură dată în date
- Participanții au fost atribuiți aleatoriu la grupuri (dacă este cazul)
- Nu există măsuri repetate (aceeași persoană testată de mai multe ori)
Ce să faci dacă este încălcat: Dacă ai măsuri repetate, folosește ANOVA cu măsuri repetate în schimb.
2. Normalitatea Reziduurilor
Ce înseamnă: Variabila dependentă ar trebui să fie aproximativ distribuită normal în fiecare grup.
Cum să verifici în Excel:
Metoda 1: Histograme (Vizuale, rapide)
- Creează histograme pentru fiecare grup
- Caută distribuții aproximativ în formă de clopot
- Asimetria sau extremele evidente sunt semnale de alarmă
Metoda 2: Regula empirică (Pentru n > 30 per grup)
- Cu eșantioane mari (n > 30 per grup), ANOVA este robust la încălcări minore
- Verifică vizual dacă distribuțiile nu sunt extrem de asimetrice
Ce să faci dacă este încălcat:
- Transformă datele (log, rădăcină pătrată)
- Folosește un test non-parametric (testul Kruskal-Wallis)
- Cu n > 30 per grup și dimensiuni de grup egale, ANOVA este de obicei OK
3. Omogenitatea Varianței (Omoscedasticitate)
Ce înseamnă: Varianța variabilei dependente ar trebui să fie similară în toate grupurile.
Cum să verifici în Excel:
Test F-max (Cel mai simplu pentru Excel):
- Din tabelul Rezumat ANOVA, notează varianța fiecărui grup
- Calculează raportul F-max:
F-max = Cea mai mare varianță / Cea mai mică varianță
Regula de decizie:
- F-max < 3: Omogenitatea varianței este îndeplinită
- F-max > 3 dar < 10: Zonă gri. Continuă cu prudență dacă dimensiunile eșantioanelor sunt egale
- F-max > 10: Încălcare severă. Ia în considerare ANOVA Welch
Exemplu:
- Varianță grupa 18-25: 0.64
- Varianță grupa 26-40: 0.81
- Varianță grupa 41+: 0.36
F-max = 0.81 / 0.36 = 2.25 (< 3, deci OK)
Ce să faci dacă este încălcat:
- Transformă datele (log, rădăcină pătrată)
- Folosește ANOVA Welch (necesită SPSS sau R)
- Dacă dimensiunile eșantioanelor sunt egale și F-max < 10, ANOVA este de obicei robust

Figura 6: Lista de verificare a asumpțiilor ANOVA - verifică toate cele trei înainte de a interpreta rezultatele
Calcularea Mărimii Efectului (Eta Pătrat)
Valoarea p îți spune dacă există o diferență, dar mărimea efectului îți spune cât de mare este diferența.
De Ce Contează Mărimea Efectului
Semnificația statistică ≠ Semnificația practică
Exemplu: Cu n = 1000, o diferență minusculă poate fi semnificativă statistic (p < 0.05) dar nesemnificativă practic.
Eta pătrat (η²) măsoară proporția varianței în variabila dependentă explicată de apartenența la grup.
Cum să Calculezi Eta Pătrat în Excel
Formula:
η² = SS Între grupuri / SS Total
Pași:
- Din tabelul ANOVA, găsește:
- SS Între grupuri (ex: 31.44)
- SS Total (ex: 53.67)
- Într-o celulă goală, introdu:
=31.44/53.67 - Rezultatul este eta pătrat: η² = 0.59
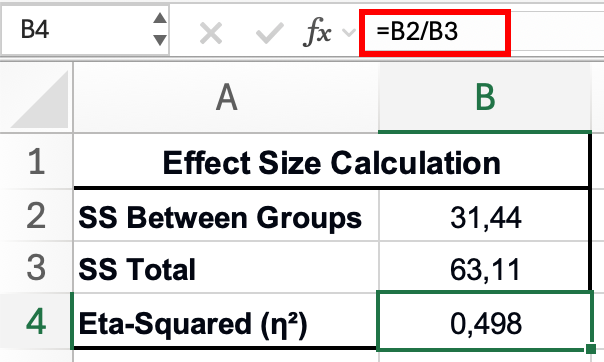 Figura 7: Calcularea eta-pătrat (mărimea efectului) din rezultatele ANOVA
Figura 7: Calcularea eta-pătrat (mărimea efectului) din rezultatele ANOVA
Interpretarea Eta Pătrat
| Mărime Efect | Valoare η² | Interpretare |
|---|---|---|
| Mic | 0.01 - 0.06 | Apartenența la grup explică 1-6% din varianță |
| Mediu | 0.06 - 0.14 | Apartenența la grup explică 6-14% din varianță |
| Mare | ≥ 0.14 | Apartenența la grup explică 14%+ din varianță |
Tabel 3: Linii directoare pentru interpretarea eta pătrat (Cohen, 1988)
Exemplul nostru: η² = 0.59 înseamnă că grupa de vârstă explică 59% din varianța în satisfacție. Aceasta este o mărime extrem de mare a efectului.
Teste Post-Hoc: Care Grupuri Diferă?
ANOVA îți spune că grupurile diferă, nu care grupuri diferă.
Dacă ANOVA este semnificativ (p < 0.05), trebuie să efectuezi teste post-hoc pentru a identifica perechi specifice care diferă.
Teste T Perechi cu Corecția Bonferroni
Deoarece Excel nu are instrumente post-hoc încorporate, folosește teste t perechi cu corecția Bonferroni pentru a controla rata de eroare.
Corecția Bonferroni:
Alpha ajustat = 0.05 / Număr de comparații
Pentru 3 grupuri:
- Număr de comparații = 3 (Grup 1 vs 2, Grup 1 vs 3, Grup 2 vs 3)
- Alpha ajustat = 0.05 / 3 = 0.017
Regulă de decizie: O comparație pe perechi este semnificativă doar dacă p < 0.017 (NU 0.05).
Cum să Efectuezi Teste T Perechi în Excel
Pentru fiecare pereche de grupuri:
- Analiză de date → Test t: Două eșantioane presupunând varianțe egale
- Interval variabil 1: Selectează date Grup 1 (fără antet)
- Interval variabil 2: Selectează date Grup 2 (fără antet)
- Diferență medie ipotetizată: 0
- Alpha: 0.05 (dar compară cu 0.017)
- Click pe OK
Repetă pentru toate cele 3 perechi:
- Vârsta 18-25 vs Vârsta 26-40
- Vârsta 18-25 vs Vârsta 41+
- Vârsta 26-40 vs Vârsta 41+
Exemplu de Rezultate Post-Hoc
| Comparație | Diferență Medie | Valoare p | Semnificativ? (p < 0.017) |
|---|---|---|---|
| 18-25 vs 26-40 | -0,9 | 0,004 | Da |
| 18-25 vs 41+ | -1,1 | 0,001 | Da |
| 26-40 vs 41+ | -0,2 | 0,234 | Nu |
Tabel 4: Rezultate ale comparațiilor post-hoc perechi cu corecția Bonferroni
Interpretare:
- Grupa 18-25 a obținut scoruri semnificativ mai mici decât grupele 26-40 (p = 0.004) și 41+ (p = 0.001)
- Grupele 26-40 și 41+ nu au diferit semnificativ una de alta (p = 0.234)
Raportarea Rezultatelor ANOVA în Format APA
Raportează rezultatele ANOVA în formatul APA standard pentru teza/disertația ta.
1. Statistici Descriptive
Tabel 5: Statistici Descriptive pentru Scorurile de Satisfacție pe Grupele de Vârstă
| Grupa de Vârstă | n | M | SD |
|---|---|---|---|
| 18-25 ani | 30 | 3,2 | 0,8 |
| 26-40 ani | 30 | 4,1 | 0,7 |
| 41+ ani | 30 | 4,3 | 0,6 |
Notă: n = dimensiune eșantion; M = medie; SD = abatere standard
2. Rezultatul Principal ANOVA
O ANOVA cu un factor a fost efectuată pentru a compara scorurile de satisfacție între cele trei grupe de vârstă (18-25, 26-40, 41+). Asumpția de omogenitate a varianței a fost îndeplinită (F-max = 2.25). ANOVA a relevat diferențe semnificative în scorurile de satisfacție între grupele de vârstă, F(2, 87) = 61.60, p < .001, η² = 0.59, indicând o mărime extrem de mare a efectului.
Componentele cheie:
- Raportează statistica F cu grade de libertate: F(df între, df în interiorul) = valoare F
- Raportează valoarea p (dacă p < 0.001, raportează ca p < .001)
- Include mărimea efectului (η²)
- Rotunjește F la 2 zecimale, p la 3 zecimale, η² la 2 zecimale
3. Rezultate Post-Hoc (dacă ANOVA este semnificativ)
Comparațiile post-hoc folosind corecția Bonferroni au indicat că grupa de vârstă 18-25 (M = 3.2, SD = 0.8) a obținut scoruri semnificativ mai mici decât atât grupa de vârstă 26-40 (M = 4.1, SD = 0.7, p = .004) cât și grupa de vârstă 41+ (M = 4.3, SD = 0.6, p = .001). Grupele 26-40 și 41+ nu au diferit semnificativ una de alta (p = .234).
Exemplu Complet (Secțiunea Rezultate)
Diferențe de Satisfacție între Grupele de Vârstă
Statisticile descriptive sunt prezentate în Tabelul 5. O ANOVA cu un factor a fost efectuată pentru a compara scorurile de satisfacție între cele trei grupe de vârstă (18-25, 26-40, 41+). Asumpția de omogenitate a varianței a fost îndeplinită (F-max = 2.25). ANOVA a relevat diferențe semnificative în scorurile de satisfacție între grupele de vârstă, F(2, 87) = 61.60, p < .001, η² = 0.59, indicând o mărime extrem de mare a efectului.
Comparațiile perechi post-hoc folosind corecția Bonferroni au relevat că grupa de vârstă 18-25 (M = 3.2, SD = 0.8) a obținut scoruri semnificativ mai mici decât atât grupa de vârstă 26-40 (M = 4.1, SD = 0.7, p = .004) cât și grupa de vârstă 41+ (M = 4.3, SD = 0.6, p = .001). Grupele 26-40 și 41+ nu au diferit semnificativ una de alta (p = .234). Aceste rezultate sugerează că satisfacția clienților crește odată cu vârsta, clienții mai tineri (18-25) raportând o satisfacție mai scăzută decât grupele de vârstă mai înaintată.
Greșeli Comune ANOVA de Evitat
1. Efectuarea multiplelor teste t în loc de ANOVA
- ✗ Greșit: Efectuarea testelor t pentru toate perechile fără corecție
- ✓ Corect: Folosește ANOVA mai întâi, apoi teste post-hoc
2. Neîndeplinirea asumpțiilor
- ✗ Greșit: Efectuarea ANOVA fără verificare
- ✓ Corect: Testează normalitatea și omogenitatea varianței
3. Raportarea doar valorilor p
- ✗ Greșit: „Grupurile au diferit semnificativ (p < .05)"
- ✓ Corect: Raportează statistica F, grade de libertate, valoarea p ȘI mărimea efectului
4. Oprirea după ce ANOVA este semnificativ
- ✗ Greșit: Concluzia „grupurile diferă" fără a identifica ce perechi
- ✓ Corect: Efectuează teste post-hoc pentru a identifica diferențele specifice
5. Folosirea ANOVA pentru două grupuri
- ✗ Greșit: ANOVA cu 2 grupuri
- ✓ Corect: Folosește test t pentru eșantioane independente pentru 2 grupuri
Rezolvarea Problemelor Comune
„Butonul Analiză de date lipsește"
- Soluție: Activează Analysis ToolPak (vezi secțiunea Cerințe Prealabile)
„Intervalul de intrare conține date non-numerice"
- Soluție: Asigură-te că toate celulele de date conțin doar numere, fără text
- Elimină orice celule goale din coloanele de date
„Statistica F este foarte mică (aproape de 1)"
- Interpretare: Mediile grupurilor sunt similare. Nu există diferențe semnificative așteptate
- Verifică dacă ai selectat intervalul corect de date
„Valoarea p apare ca notație științifică (1.2E-05)"
- Interpretare: Aceasta înseamnă p = 0.000012, ceea ce este < 0.001 (extrem de semnificativ)
- Raportează ca p < .001 în format APA
„Varianțele sunt foarte inegale (F-max > 10)"
- Soluție 1: Transformă datele (transformare logaritmică sau rădăcină pătrată)
- Soluție 2: Folosește ANOVA Welch (necesită R sau SPSS)
- Soluție 3: Raportează încălcarea și continuă cu prudență dacă dimensiunile eșantioanelor sunt egale
Pașii Următori: Dincolo de ANOVA cu Un Factor
Notă: Următoarele tehnici avansate ANOVA necesită software statistic precum SPSS sau R (Data Analysis ToolPak din Excel acceptă doar ANOVA cu un factor).
Dacă ai două variabile independente:
- Folosește ANOVA cu doi factori pentru a testa efectele principale și interacțiunile
Dacă ai măsuri repetate:
- Folosește ANOVA cu măsuri repetate (aceiași participanți testați de mai multe ori)
Dacă asumpțiile sunt încălcate sever:
- Folosește testul Kruskal-Wallis (alternativă non-parametrică)
Pentru fluxul complet de analiză a chestionarelor:
- Vezi ghidul nostru: Cum să Analizezi Datele din Chestionar în Excel: Ghid Complet
Întrebări Frecvente
Concluzie
ANOVA cu un factor în Excel este direct folosind Data Analysis ToolPak:
- Organizează datele în coloane (una per grup)
- Efectuează Anova: Factor Unic prin Analiză de date
- Verifică asumpțiile (independență, normalitate, omogenitatea varianței)
- Interpretează rezultatele (statistica F și valoarea p)
- Calculează mărimea efectului (eta-pătrat)
- Efectuează teste post-hoc (corecția Bonferroni) dacă este semnificativ
- Raportează în format APA cu statistici descriptive
Concluzia cheie: ANOVA îți spune că grupurile diferă. Testele post-hoc îți spun care grupuri diferă. Raportează întotdeauna atât semnificația statistică (valoarea p) cât și semnificația practică (mărimea efectului).
Pentru compararea doar a două grupuri, folosește Test T în Excel: Ghid Complet. Pentru a decide între test t și ANOVA, vezi Test T vs ANOVA: Care Test Să Folosești?