ในบทความนี้ เราจะศึกษาวิธีการวิเคราะห์ตัวแปรคั่นกลางโดยใช้โปรแกรม SPSS และเรียนรู้การตีความผลลัพธ์เพื่อนำไปประยุกต์ใช้ในงานวิจัยของเราค่ะ คุณจะได้เรียนรู้วิธีการวิเคราะห์ทั้งสองแบบ: วิธีแรกคือการใช้เครื่องมือสถิติมาตรฐานที่มีอยู่ใน SPSS และวิธีที่สองคือการใช้โปรแกรมเสริม PROCESS เพื่อทำการวิเคราะห์ที่ง่ายและรวดเร็วขึ้น
สิ่งที่คุณจะเรียนรู้
เมื่อคุณศึกษาบทความนี้จนจบ คุณจะสามารถทำความเข้าใจได้ว่า:
- การวิเคราะห์ตัวแปรคั่นกลางในการวิจัยทางสถิติคืออะไร
- วิธีการวิเคราะห์ตัวแปรคั่นกลางใน SPSS ด้วยสองวิธีที่กล่าวมา
- วิธีการประเมินผลกระทบทางอ้อมด้วยการทดสอบ Sobel Test
- วิธีการคำนวณผลกระทบโดยตรงในการวิเคราะห์ตัวแปรคั่นกลาง
- วิธีการตีความผลลัพธ์ของการวิเคราะห์ตัวแปรคั่นกลางใน SPSS
เพื่อการฝึกปฏิบัติที่ง่ายขึ้น ชุดข้อมูลตัวอย่างสำหรับการวิเคราะห์ตัวแปรคั่นกลางได้ถูกเตรียมให้คุณแล้ว คุณสามารถฝึกทีละขั้นตอนบนคอมพิวเตอร์ของคุณได้เลยค่ะ
ตัวแปรคั่นกลางคืออะไร
ตัวแปรคั่นกลางคือตัวแปรที่ทำหน้าที่เป็นสะพานเชื่อมระหว่างตัวแปรอิสระ (สาเหตุ) กับตัวแปรตาม (ผลลัพธ์) ในการศึกษาหรือการวิจัย มันช่วยอธิบายว่าทำไมหรืออย่างไรตัวแปรหนึ่งถึงส่งผลต่ออีกตัวแปรหนึ่ง
ยกตัวอย่างเช่น ถ้าเรากำลังศึกษาว่าการออกกำลังกาย (ตัวแปรอิสระ) ช่วยลดน้ำหนัก (ตัวแปรตาม) อย่างไร ตัวแปรคั่นกลางอาจเป็นการเปลี่ยนแปลงในการเผาผลาญพลังงาน (ตัวแปรคั่นกลาง) การออกกำลังกายทำให้การเผาผลาญพลังงานเพิ่มขึ้น ซึ่งก็จะช่วยลดน้ำหนักได้ ในที่นี้ การเผาผลาญพลังงานเป็น “สะพาน” ที่เชื่อมการออกกำลังกายกับการลดน้ำหนัก
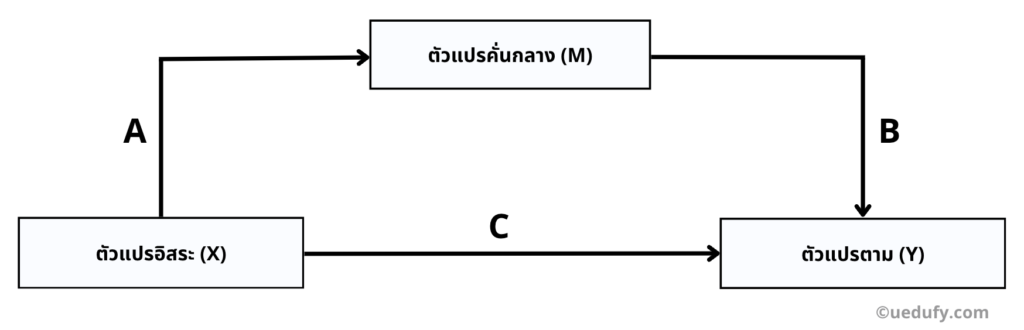
- เส้นทาง A: ผลกระทบของตัวแปรอิสระ (X) ต่อตัวแปรคั่นกลาง (M)
- เส้นทาง B: ผลกระทบของตัวแปรคั่นกลาง (M) ต่อตัวแปรตาม (Y)
- เส้นทาง C: ผลกระทบโดยตรงของตัวแปรอิสระ (X) ต่อตัวแปรตาม (Y)
ในการวิเคราะห์นี้ เราจะพยายามหาว่ามีการเชื่อมโยงทางอ้อมระหว่างตัวแปรอิสระและตัวแปรตามผ่านตัวแปรคั่นกลางหรือไม่ ซึ่งถูกแสดงด้วยเส้นทาง A และ B โดยเราจะใช้ค่า Unstandardized Coefficient Beta และ Standard Error เพื่อประเมินการเชื่อมโยงทางอ้อมในเส้นทาง A และ B ในขณะที่เส้นทาง C คือการเชื่อมโยงทางตรง
ในการวิจัยที่เราทำการวิเคราะห์ตัวแปรคั่นกลาง สิ่งสำคัญคือเราต้องมั่นใจว่าตัวแปรที่เรากำลังศึกษานั้นเกี่ยวข้องกันอยู่แล้วในระดับหนึ่ง หมายความว่าตัวแปรอิสระ (X) ที่เราสนใจต้องมีการเชื่อมโยงหรือมีผลกระทบบางอย่างต่อตัวแปรตาม (Y) ที่เราต้องการทราบผลลัพธ์ ถ้าหากไม่มีความสัมพันธ์เลย คือไม่สามารถพบว่า X มีผลใดๆ ต่อ Y แล้ว นั่นก็หมายความว่าเราไม่สามารถใช้ตัวแปรคั่นกลาง (M) เพื่ออธิบายว่า X ส่งผลต่อ Y ได้อย่างไร
ความแตกต่างระหว่างตัวแปรคั่นกลางกับตัวแปรควบคุม
ตัวแปรคั่นกลางคือตัวแปรที่เป็นสะพานในการเชื่อมโยงระหว่างตัวแปรอิสระและตัวแปรตาม ในขณะที่ตัวแปรกำกับคือตัวแปรที่เราคงค่าไว้เพื่อตรวจสอบผลกระทบที่แท้จริงของตัวแปรอิสระต่อตัวแปรตามในข้อมูลนั้น สามารถอ่านบทความเกี่ยวกับการวิเคราะห์ตัวแปรกำกับ การวิเคราะห์ตัวแปรคั่นกลางจะช่วยให้เราเข้าใจการเชื่อมโยงทางอ้อมระหว่างตัวแปรอิสระ (X) กับตัวแปรตาม (Y) ผ่านตัวแปรที่เรียกว่าตัวแปรคั่นกลาง (M) ได้ ซึ่งจะมีค่าเชื่อมโยงที่แสดงอยู่ในเส้นทาง A และ B ของแผนภาพ ส่วนเส้นทาง C แสดงถึงค่าเชื่อมโยงทางตรงจากตัวแปรอิสระไปยังตัวแปรตามโดยตรง
ในการศึกษาต่อไป คุณจะได้เรียนรู้การวิเคราะห์ตัวแปรคั่นกลาง การประเมินผลกระทบทางอ้อม และวิธีการตีความผลลัพธ์เหล่านี้ พร้อมทั้งการฝึกฝนด้วยชุดข้อมูลตัวอย่างใน SPSS เพื่อให้คุณได้ประสบการณ์จริงในการทำการวิเคราะห์ค่ะ
ตัวอย่างการวิเคราะห์ตัวแปรคั่นกลาง
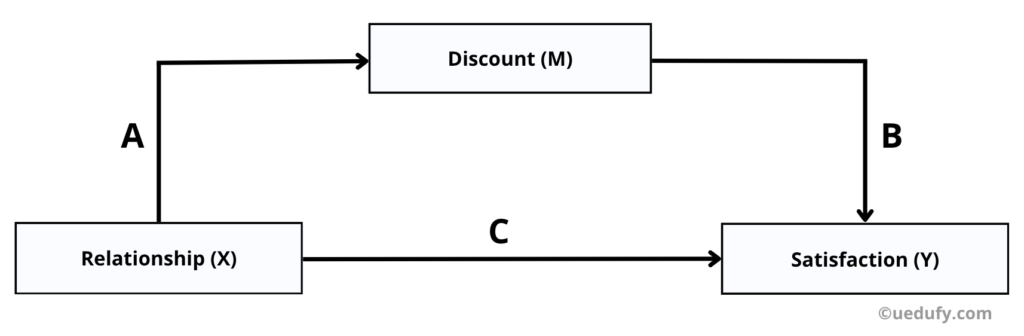
สมมุติว่าเราต้องการทดสอบสมมติฐานการวิจัยที่ระบุว่า “ผลกระทบระหว่างความสัมพันธ์และความภักดีสามารถลดลงได้ด้วยส่วนลด”
ในตัวอย่างนี้ “ความสัมพันธ์” คือตัวแปรอิสระ (X) “ความภักดี” คือตัวแปรตาม (Y) และ “ส่วนลด” คือตัวแปรคั่นกลาง (M)
| Variable name | Variable type | Notation |
| Relationship (ความสัมพันธ์) | Independent variable (ตัวแปรอิสระ) | X |
| Satisfaction (ความพึงพอใจ) | Dependent variable (ตัวแปรตาม) | Y |
| Discounts (ส่วนลด) | Mediator variable (ตัวแปรคั่นกลาง) | M |
วัตถุประสงค์ของเราคือ การวิเคราะห์เพื่อทดสอบนัยสำคัญทางสถิติสำหรับผลกระทบทางอ้อม (เส้นทาง A * B)
ขอแนะนำให้ดาวน์โหลดชุดข้อมูลวิธีการวิเคราะห์ตัวแปรคั่นกลางใน SPSS ที่นี่นะคะ
และฝึกฝนไปพร้อมๆ กันค่ะ ไฟล์ข้อมูลเป็นเพียงแค่การจำลองและควรใช้เพื่อการศึกษาเท่านั้นค่ะ
วิธีที่ 1: การประมวลผลการวิเคราะห์ตัวแปรคั่นกลางในโปรแกรม SPSS
การเตรียมข้อมูล:คุณต้องดาวน์โหลดชุดข้อมูลตัวอย่างจากลิงค์ที่ให้ไว้ แล้วเปิดไฟล์นั้นในโปรแกรม SPSS เพื่อให้สามารถทำการวิเคราะห์ได้
- การวิเคราะห์ผลกระทบโดยตรงระหว่างตัวแปร X และ Y
- ขั้นตอนแรกในการวิเคราะห์คือการตรวจสอบว่ามีผลกระทบที่มีความหมายทางสถิติระหว่างตัวแปรอิสระ (X) กับตัวแปรตาม (Y) หรือไม่
- ถ้าไม่มีผลกระทบทางสถิติที่มีนัยสำคัญ นั่นหมายความว่าการวิเคราะห์ตัวแปรคั่นกลางอาจไม่จำเป็น
- คุณสามารถตรวจสอบสิ่งนี้ได้โดยการทำการวิเคราะห์ถดถอยเชิงเส้น (linear regression) ซึ่งเป็นวิธีสถิติที่ใช้เพื่อทำนายค่าของตัวแปรตาม (Y) จากตัวแปรอิสระ (X)
การเข้าสู่เมนูการวิเคราะห์ใน SPSS: คุณทำได้โดยคลิกที่เมนูบาร์ใน SPSS ไปที่ ‘Analyze’ จากนั้นเลือก ‘Regression’ และคลิก ‘Linear’
จากกล่องด้านซ้าย ให้ย้ายตัวแปร Relationship ไปยังบล็อกด้านขวาและตัวแปร Satisfaction ไปยังบล็อกด้านขวาทางด้านซ้าย โดยใช้ปุ่มลูกศรระหว่างบล็อกช่วยในการย้าย
คลิกปุ่ม OK เพื่อดำเนินการวิเคราะห์การถดถอยเชิงเส้นระหว่าง X และ Y
ตรวจสอบค่า p-value ในตาราง Coefficients , ให้ดูค่า Sig ซึ่งพบว่า ค่า p ≤ 0.05
ดังนั้น ผลกระทบรวมทั้งหมดจึงมีนัยสำคัญ เนื่องจาก ค่า Sig เท่ากับ 0.000 ซึ่งน้อยกว่าค่า p ≤ 0.05
- ผลกระทบรวมนัยสำคัญในโปรแกรม SPSS
การประมาณการผลกระทบทางตรงของ X ต่อ M เพื่อหาค่า Beta coefficient และ Standard Error เพื่อวิเคราะห์เส้นทาง A ซึ่งเป็นข้อกำหนดที่จำเป็นสำหรับการคำนวณผลกระทบทางอ้อม
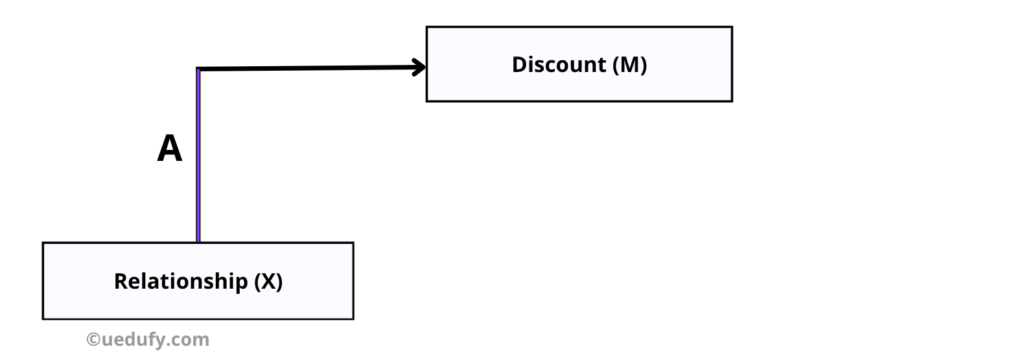
โดยมีขั้นตอนในการปฎิบัติดังนี้
- ในโปรแกรม SPSS คุณจะเริ่มต้นด้วยการไปที่เมนู ‘Analyze‘ ซึ่งอยู่บนแถบเมนูด้านบนของหน้าต่างโปรแกรม
- เลื่อนเมาส์ไปที่ ‘Regression‘ ซึ่งจะเปิดเมนูย่อยออกมา
- จากเมนูย่อยที่เปิดออกมา คลิกเลือก ‘Linear‘ เพื่อเริ่มการวิเคราะห์ถดถอยเชิงเส้น
- ถ้าคุณมีการวิเคราะห์ก่อนหน้านี้ที่ยังค้างอยู่ คลิกที่ปุ่ม ‘Reset’ เพื่อล้างข้อมูลการคำนวณเหล่านั้นออกไป
- หลังจากนั้นคุณจะเพิ่มตัวแปร ‘Discount’ ไปยังกล่อง ‘Dependent’ เพื่อกำหนดให้เป็นตัวแปรตามที่คุณต้องการทำนายค่า
- และเพิ่มตัวแปร ‘Relationship’ ไปยังกล่อง ‘Independent’ เพื่อกำหนดให้เป็นตัวแปรอิสระที่คุณคาดว่าจะมีผลต่อตัวแปรตาม
- หลังจากเพิ่มตัวแปรทั้งหมดไปยังกล่องที่เหมาะสมแล้ว คลิก OK เพื่อที่โปรแกรมจะทำการวิเคราะห์ข้อมูลตามที่คุณกำหนด
ตาราง Coefficients แสดงผลผลกระทบทางตรงของ X ต่อ M ว่ามีนัยสำคัญ (ค่า p 0.000) ค่า Unstandardized Coefficient Beta เท่ากับ (.413) และ Std Error เท่ากับ (.084) อย่าลืมบันทึกค่าที่ได้จากการวิเคราะห์ครั้งนี้ด้วยนะคะ
- การประมาณค่าผลกระทบทางตรงของ X และ M ที่มีต่อ Y
ในขั้นตอนนี้ เราจะประมวลผลทางตรงระหว่าง X และ Y และ M และ Y เพื่อหา ค่า Unstandardized Beta และ Standard Error coefficients ของเส้นทาง B และ C
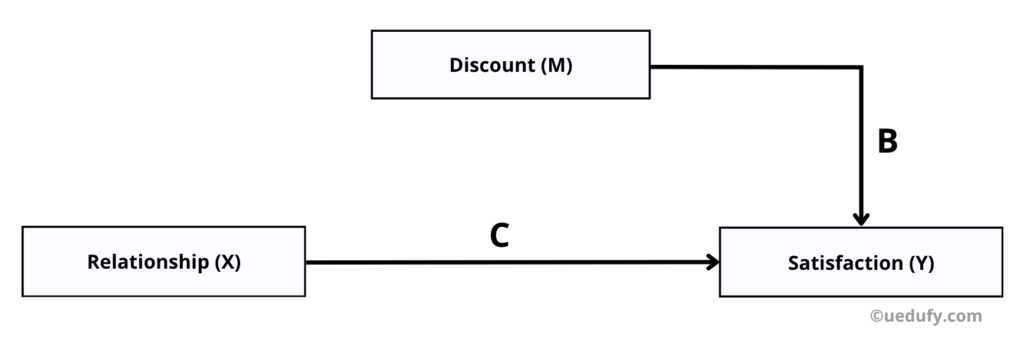
นับจากนี้เราใช้ตัวทำนายสองตัว (X และ M) เราจะใช้การวิเคราะห์การถดถอยเชิงพหุคูณ
คลิก Analyze → Regression → Linear. คลิกเลือก Reset เพื่อลบข้อมูลก่อนหน้านี้
เพิ่ม ตัวแปร Satisfaction ไปยังกล่อง Dependent ตัวแปร Relationship และ Discounts ไปยังกล่อง Independent
ตาราง Coefficients แสดงผลกระทบทางอ้อมพบว่า Unstandardized Coefficient Beta เท่ากับ (.733) และ Std. Error เท่ากับ (.043)
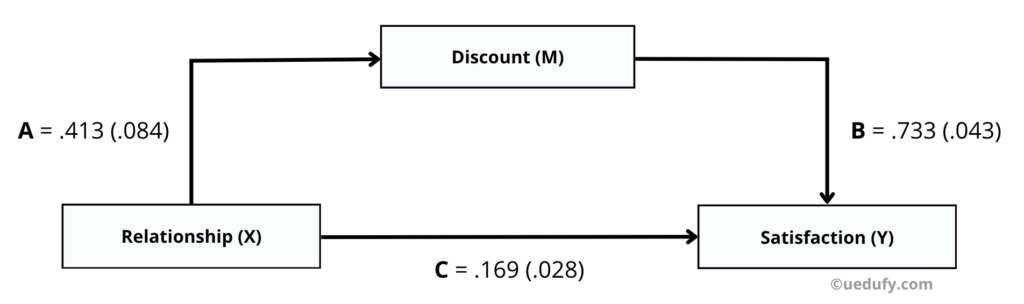
หลังจากการประมวลผลทางอ้อม เราได้ค่า coefficients ทั้งหมดซึ่งสรุปค่าสัมประสิทธิ์ ไว้ดังภาพ
Path A = .413 (.084)
Path B = .733 (.043)
Path C = .169 (.028)
- การทดสอบผลกระทบทางอ้อมเพื่อนัยสำคัญทางสถิติ
เพื่อทดสอบว่าผลกระทบทางอ้อมในตัวอย่างของเรามีนัยสำคัญทางสถิติหรือไม่ เราสามารถใช้ bootstrapping หรือ Sobel Test ทำการทดสอบได้
ในการทดสอบนี้สามารถใช้ Sobel Test กับโปรแกรมเสริม PROCESS ซึ่งจะอธิบายไว้ในวิธีที่ 2 การวิเคราะห์ตัวแปรคั่นกลางกับโปรแกรมเสริม PROCESS ใน SPSS
การทดสอบโซเบลเป็นวิธีการที่ใช้ในการประมาณความสำคัญทางสถิติสำหรับผลกระทบทางอ้อมในการวิเคราะห์ตัวแปรคั่นกลาง ซึ่งในโปรแกรม SPSS ไม่มีฟังก์ชั่นการทดสอบ Sobel แต่สามารถทำได้ง่ายๆ ด้วยเครื่องคิดเลข Sobel Test บนออนไลน์ คลิกเพื่อลิงค์ไปหน้าคำนวณการทดสอบโซเบล HERE.
เพียงเพิ่มค่า Unstandardized Coefficient Beta ของ A และ B และ ค่า Std
และเพิ่มค่า Error coefficients ของ A และ B ในช่อง sa และ sb แสดงไว้ดังภาพนี้
คลิกปุ่มคำนวณ ผลการทดสอบ Sobel Test จะแสดงไว้ในแถวแรกตามที่ไฮไลท์ ดังภาพ
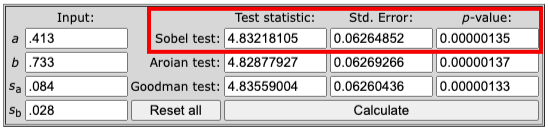
และผลการวิเคราะห์ผลกระทบทางอ้อมสำหรับ X → M → X โดยใช้ Sobel Test มีดังนี้:
Test statistic = 4.83218105
Std. Error = 0.06264852
p-value = 0.00000135
ให้ดูที่ค่า p-value ซึ่งในกรณีนี้น้อยกว่า 0.05 ดังนั้นเราจึงสรุปได้ว่า มีผลกระทบทางอ้อมระหว่างตัวแปรความสัมพันธ์ (Relationship) และตัวแปรความพึงพอใจ (Satisfaction) ผ่านตัวแปรส่วนลด (Discount) มีนัยสำคัญทางสถิติ (p-value ≤ 0.05)
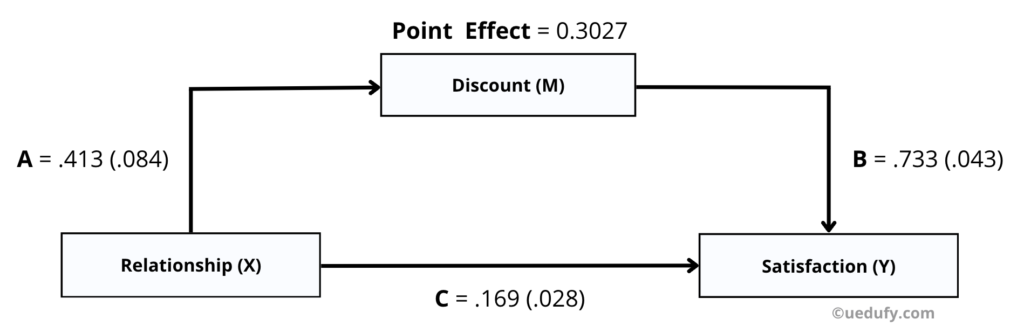
หากต้องการทราบการประมาณค่าจุดของผลกระทบทางอ้อม สามารคำนวณ Unstandardized Coefficient Beta ของเส้นทาง A * B ดังนี้:
0.413 * 0.733 = 0.3027
0.3027 เป็นค่าประมาณของผลกระทบทางอ้อมระหว่างความสัมพันธ์และความพึงพอใจผ่านตัวแปรส่วนลดที่ค่า p ที่ 0.00000135 ตามที่แสดงในการทดสอบ Sobel
วิธีที่ 2: การวิเคราะห์ตัวแปรคั่นกลางในโปรแกรม SPSS โดยการใช้โปรแกรมเสริม Process
เริ่มต้นจากการติดตั้งโปรแกรมเสริม PROCESS ใน SPSS. ซึ่งขั้นตอนการติดตั้งง่ายและใช้เวลาไม่เกิน 5 นาที
- เปิดโปรแกรมเสริม Process Macro
เมื่อติดตั้งแล้วจะพบว่า PROCESS Macro ติดตั้งอยู่ในส่วน Analyze → Regression → PROCESS v.x by Andrew F. Hayes.
- เพิ่มตัวแปรความพึงพอใจ (Satisfaction) ในบล็อกตัวแปร Y และตัวแปรความสัมพันธ์ (Relationship) ลงในบล็อกตัวแปร X และตัวแปรคั่นกลาง คือ ตัวแปรส่วนลด (Discounts)
เลือกหมายเลข 4 ในช่อง Model number
โดยค่าเริ่มต้น PROCESS Macro สำหรับชื่อตัวแปรโปรแกรมจะไม่ยอมรับอักขระมากกว่า 8 ตัวซึ่งเราสามารถเปลี่ยนชื่อตัวแปรใน SPSS ให้สั้นลงได้
- คลิกปุ่ม Options
ตรวจสอบให้แน่ใจด้วยนะคะ ว่าได้เลือก “ Show total effect model (only models 4, 6, 80, 81, 82) (เฉพาะรุ่น 4, 6, 80, 81, 82)” และ “Standardized effects (mediation-only models)” ไว้แล้ว ดังภาพ
คลิก Continue และคลิก OK เพื่อวิเคราะห์ตัวแปรคั่นกลางในโปรแกรม SPSS
วิธีการอ่านค่าประมวลการวิเคราะห์ตัวแปรคั่นกลางใน SPSS
ส่วนแรกของผลการวิเคราะห์ตัวแปรคั่นกลางด้วย PROCESS จะแสดงภาพรวมของการวิเคราะห์ตัวแปรคั่นกลางตามลำดับตัวแปร X, Y และ M
เราสามารถเห็นผลทางตรงตัวแปรทำนายระหว่างตัวแปรความสัมพันธ์ (Relationship) (ค่า P = 0.000) กับ ตัวแปรส่วนลด (Discounts) มีนัยสำคัญ (ค่า P ≤ 0.05)
ถัดมา เราสามารถสังเกตผลกระทบระหว่างตัวแปรความสัมพันธ์ (Relationship) (ค่า P = 0.000) กับ ส่วนลด (Discounts) (ค่า P = 0.000) ต่อความพึงพอใจ (Satisfaction) มีนัยสำคัญ (ค่า P ≤ 0.05)
สุดท้าย ตรวจสอบผลกระทบทางอ้อมของ X ต่อ Y ผ่านตัวแปรคั่นกลาง M โดยมีจุดผลกระทบคำนวณได้ 0.3030
การวิเคราะห์ตัวแปรคั่นกลางด้วยวิธีที่ 1 และ 2 มีความคล้ายคลึงกัน โดยมีความแตกต่างเพียงอย่างเดียวคือจุดกระทบทางอ้อมที่ปัดเศษขึ้นจาก 0.3027 เป็น 0.3030 ในโปรแกรมเสริม PROCESS Macro
สรุป
เป็นการเกริ่นถึงเทคนิคทางสถิติอื่นๆ เช่น Structural Equation Modeling (SEM) หรือ การวิเคราะห์เส้นทางที่ต้องใช้โปรแกรม AMOS ในการวิเคราะห์ข้อมูล
สุดท้าย หากคุณพบว่าบทเรียนสถิตินี้มีประโยชน์ โปรดแชร์บทความของเราให้เพื่อนของคุณอ่านด้วยนะคะ
เอกสารอ้างอิง
Sobel, M. E. (1982). Asymptotic intervals for indirect effects in structural equations models. In S. Leinhart (Ed.), Sociological methodology 1982 (pp.290-312). San Francisco: Jossey-Bass.

