สวัสดีค่ะ! บทเรียนนี้เราจะสาธิตการทดสอบสถิติด้วย t-test ใน Excel ค่ะหากคุณรู้สึกว่าเรื่องนี้ยาก เรามีวิธีการสอนที่จะทำให้คุณเข้าใจและสามารถนำไปใช้งานได้จริงค่ะ ไม่ว่าจะเป็นการทำงานหรือวิจัย บทเรียนนี้จะช่วยให้คุณเข้าใจวิธีการทำงานของ t-test และสูตรการคำนวณที่ใช้ในการวิเคราะห์ t-test ใน Excel นอกจากนั้นคุณสามารถอ่าน ความหมาย T-test ก่อนเข้าสู่บทเรียนนี้
คุณสามารถดาวน์โหลดชุดข้อมูลตัวอย่างที่เราจัดเตรียมไว้ใน Excel ที่นี้ ซึ่งเป็นเครื่องมือที่ใช้ในการฝึกฝนและเรียนไปด้วยกันนะคะ
หลังจากเรียนบทเรียนนี้ คุณจะเข้าใจเกี่ยวกับ
- การใช้งานและการประยุกต์ใช้ t-test
- สูตรการคำนวณและวิธีการใช้ t-test ใน Excel
วิธีการคำนวณการทดสอบ t-Test ใน Excel จะสาธิตการปฏิบัติ T-Test ทั้ง 3 ประเภท ดังนี้
การทดสอบ One-Sample T-Test ใน Excel
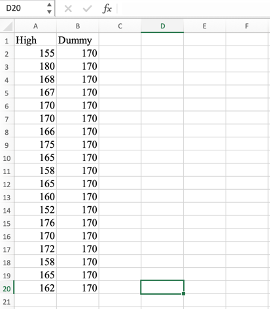
Step 1: สร้างชุดข้อมูลใน Excel เพื่อทดสอบ One-Sample T-Test
จากตัวอย่างเป็นส่วนสูงและใช้ Dummy ใน Excel โดยสมมุติว่าคุณมีชุดข้อมูลของส่วนสูงของนักเรียนในห้องเรียนหนึ่ง และคุณต้องการทดสอบว่ามีความแตกต่างอย่างมีนัยสำคัญทางสถิติในส่วนสูงหรือไม่ ในสถานการณ์นี้ Dummy คือตัวแปรที่คุณใช้เพื่อแสดงเพศของนักเรียนหรือส่วนสูง ในตัวอย่างนี้ค่า Dummy จะถูกกำหนดเป็น 170 ซึ่งเป็นส่วนสูงของนักเรียนตามสมติฐาน
- เปิดไฟล์ Excel ที่มีชุดข้อมูลของส่วนสูงนักเรียน
- ในคอลัมน์ถัดไป สร้างคอลัมน์ที่ชื่อว่า ‘Dummy’ ซึ่งจะใช้สำหรับแทนเพศของนักเรียน
- ใส่ค่า 170 ในคอลัมน์ ‘Dummy’
Step 2: ทดสอบ One-Sample T-Test ใน Excel
สมมติฐานเพื่อการทดสอบสามารถเขียนดังนี้:
H0: μ1 = 170
H1: μ1 ≠ 170
สมมติฐานหมายความว่า สมมติฐานหลัก (null hypothesis) ตั้งไว้ว่า ค่าเฉลี่ยของกลุ่มตัวอย่างแรก (μ1) เท่ากับ 170 และสมมติฐานทางเลือก (alternative hypothesis) ตั้งไว้ว่าค่าเฉลี่ยของกลุ่มตัวอย่างแรก (μ1) ไม่เท่ากับ 170.
เมื่อต้องการทำ One-Sample T-Test ใน Excel และต้องการเปรียบเทียบชุดข้อมูลกับค่าเฉลี่ยที่กำหนดคือ 170 ดังนั้นเราจะต้องใช้ฟังก์ชัน T.TEST ใน Excel ซึ่งไม่จำเป็นต้องใช้หน้าต่าง “Data Analysis” โดยมีขั้นตอนในการทดสอบดังนี้
- คลิกเซลล์ที่เราต้องการแสดงผลลัพธ์ของ t-test
- พิมพ์สูตร =T.TEST ลงในเซลล์นั้น)
- สำหรับ array1 ในสูตร ให้เลือกช่วงข้อมูล (เช่น A2:A20)
- สำหรับ array2 เราต้องใส่ช่วงข้อมูลที่มีค่าเดียวกันซ้ำๆ ในกรณีนี้คือค่าเฉลี่ยที่กำหนดที่ 170 ซึ่งเราสามารถสร้างช่วงข้อมูลนี้ใน Excel โดยการพิมพ์ 170 ลงในจำนวนเซลล์ที่เท่ากับขนาดของชุดข้อมูลของเรา
- ใส่ค่า “tails” ซึ่งควรเป็น 1 หากทำการทดสอบด้านเดียวหรือ 2 สำหรับการทดสอบสองด้าน
- ปิดวงเล็บและกด Enter เพื่อดูผลลัพธ์
ตัวอย่างสูตรที่จะอยู่ในแถบสูตร (Formula Bar) สำหรับ one-sample t-test จะเป็นเช่นนี้:
=T.TEST(A2:A20, B2:B20, 1, 1)
โดยที่ A2:A20 คือช่วงข้อมูลส่วนสูง และ B2:B20 คือช่วงข้อมูลที่เราได้สร้างขึ้นมีค่าเท่ากับ 170 ทั้งหมด ตัวเลข 1 แรกคือการทดสอบด้านเดียว และตัวเลข 1 ตัวที่สองคือการทดสอบแบบ paired
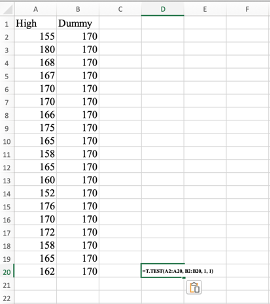
Step 3: การแสดงผลลัพธ์ของการทดสอบ t-test ใน Excel
การแสดงผลลัพธ์ของการทดสอบ t-test ใน Excel และค่าที่ได้คือ 0.01429 ซึ่งเป็นค่า p-value
ค่า p-value นี้บ่งบอกถึงความน่าจะเป็นที่ค่าเฉลี่ยของตัวอย่างที่เราทดสอบจะแตกต่างจากค่าเฉลี่ยที่เราสมมติไว้ (ในที่นี้คือ 170) หาก p-value น้อยกว่า 0.05 ซึ่งเป็นระดับนัยสำคัญทางสถิติที่ตั้งไว้ แสดงว่ามีหลักฐานเพียงพอที่จะปฏิเสธสมมติฐานหลัก (H0) และยอมรับสมมติฐานทางเลือก (H1) ที่ว่าค่าเฉลี่ยของตัวอย่างไม่เท่ากับ 170 จึงสามารถสรุปได้ว่าค่าเฉลี่ยของข้อมูลตัวอย่างแตกต่างจาก 170 อย่างมีนัยสำคัญทางสถิติ

การทดสอบค่าเฉลี่ยของสองกลุ่มที่ไม่เกี่ยวข้องกัน Independent Samples T-Test
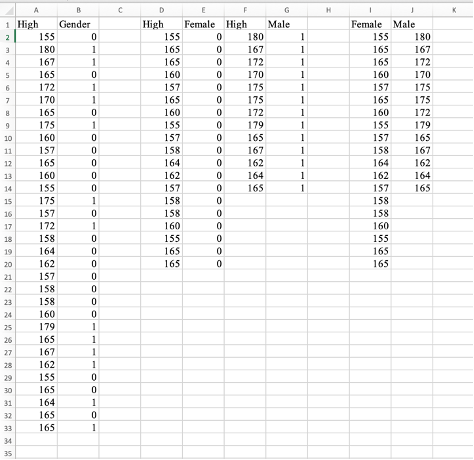
Step 1: จัดหมวดหมู่ข้อมูลใน Excel ตามกลุ่ม
เพื่อทำการทดสอบ t-test สำหรับตัวอย่างอิสระ เราจะต้องแยกข้อมูลตามกลุ่มที่เราต้องการเปรียบเทียบ ในกรณีนี้เป็นข้อมูลเกี่ยวกับส่วนสูงที่ถูกแยกตามเพศ โดยมีคอลัมน์ข้อมูลสำหรับชายและคอลัมน์ข้อมูลสำหรับหญิง และในแต่ละคอลัมน์ควรมีข้อมูลส่วนสูงที่สอดคล้องกับเพศนั้นๆหลังจากนั้น เราจะใช้ฟังก์ชัน Data Analysis ที่มีใน Excel เพื่อทำการคำนวณ t-test โดยเลือก ‘t-Test: Two-Sample Assuming Equal Variances’ หรือ ‘t-Test: Two-Sample Assuming Unequal Variances‘
Step 2: หลังจากจัดหมวดหมู่ข้อมูลใน Excel แล้ว ให้คลิกที่ ‘Data Analysis’ จากนั้นเลือก ‘t-Test: Two-Sample Assuming Unequal Variances’ และคลิก OK
การเลือก ‘t-Test: Two-Sample Assuming Unequal Variances’ หมายความว่าเรากำลังทำการทดสอบ t-test ระหว่างสองกลุ่มที่เราสมมติว่ามีความแปรปรวนไม่เท่ากัน ซึ่งเป็นความเหมาะสมในกรณีที่เราไม่สามารถสมมติฐานได้ว่าประชากรทั้งสองที่เรากำลังเปรียบเทียบมีความแปรปรวนเท่ากัน
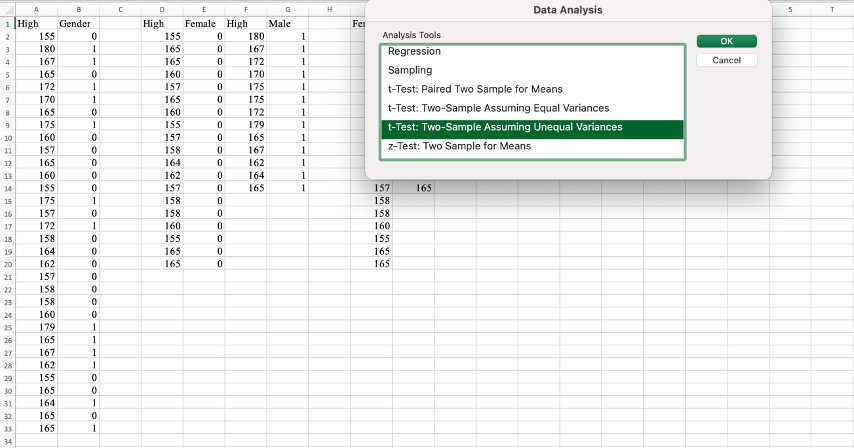
Step 3: การเลือก T-Test Two-Sample Assuming Unequal Variances
ในหน้าต่าง ‘t-Test: Two-Sample Assuming Unequal Variances’ ให้เลือกช่วงของเซลล์ที่มีข้อมูลของตัวแปรหญิงและชายที่เราต้องการนำไปใช้สูตร t-test สำหรับตัวอย่างอิสระ ไม่ต้องระบุค่าเฉลี่ยที่สมมติฐานไว้ (Hypothesized Mean Difference) จากนั้นเลือก ‘Labels’ และคลิก OK
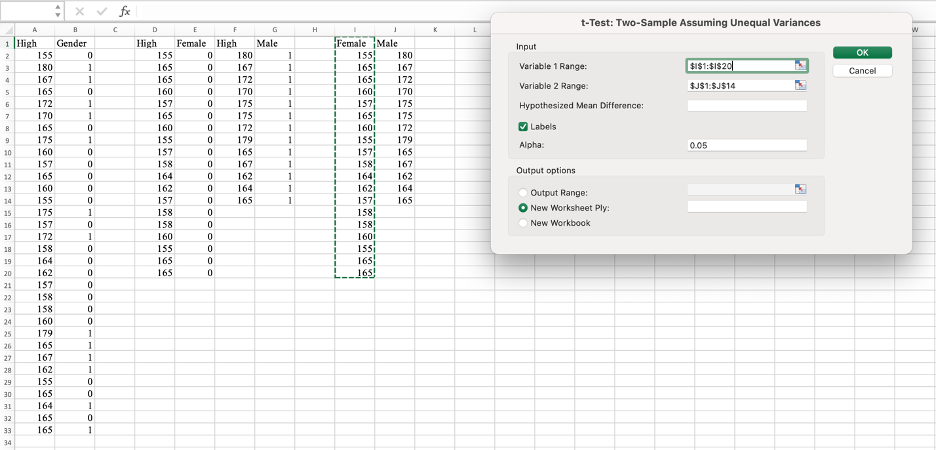
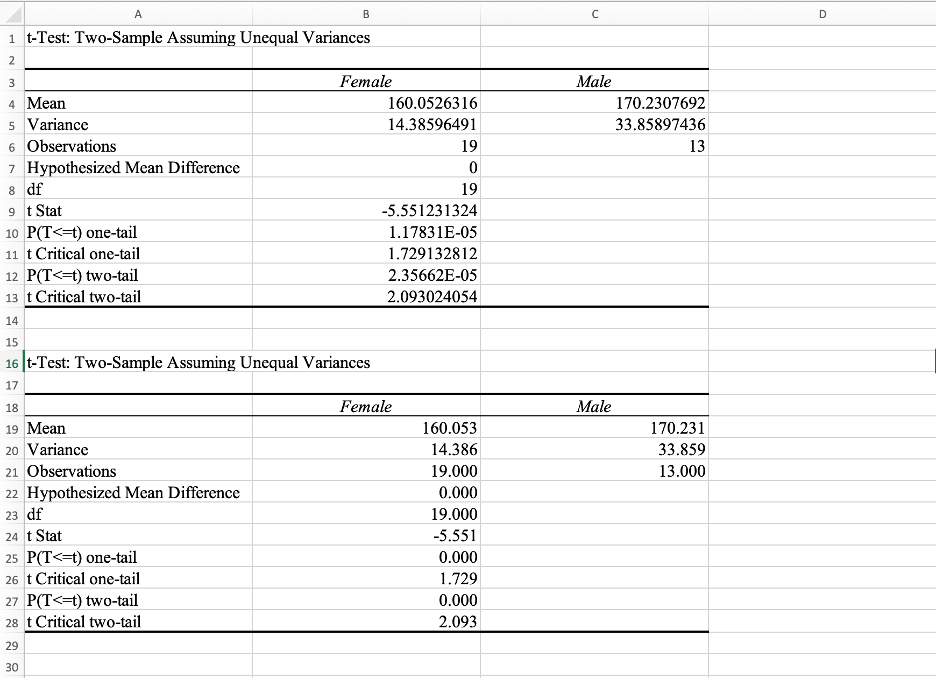
Step 4: การแสดงผลลัพธ์ของการทดสอบ t-test สำหรับตัวอย่างอิสระ (independent samples) โดยแสดงข้อมูลทั้งสำหรับกลุ่มหญิงและชาย ผลลัพธ์นี้แสดงให้เห็นว่า:
ค่าเฉลี่ยของกลุ่มหญิง (Female Mean) คือ 160.652316
ค่าเฉลี่ยของกลุ่มชาย (Male Mean) คือ 170.2307692
ค่า p-value สำหรับการทดสอบนี้คือ 2.36662E-05 ซึ่งเมื่อลดทศนิยมลงจะได้ประมาณ 0.000023 น้อยกว่า 0.05 ซึ่งปฏิเสธสมมติฐานหลัก H0 และยอมรับสมมติฐานทางเลือก H1หมายความว่ามีความแตกต่างระหว่างค่าเฉลี่ยของสองกลุ่มอย่างมีนัยสำคัญทางสถิติระหว่างส่วนสูงของชายและหญิง หรือกล่าวอีกนัยหนึ่งคือ ชายมีส่วนสูงเฉลี่ยที่สูงกว่าหญิงอย่างมีนัยสำคัญทางสถิติ
โดยการตั้งสมมติฐานสำหรับการทดสอบนี้จะเป็นดังนี้:
สมมติฐานหลัก (Null Hypothesis, H0): ไม่มีความแตกต่างระหว่างค่าเฉลี่ยของสองกลุ่ม
สมมติฐานทางเลือก (Alternative Hypothesis, H1 ): มีความแตกต่างระหว่างค่าเฉลี่ยของสองกลุ่ม
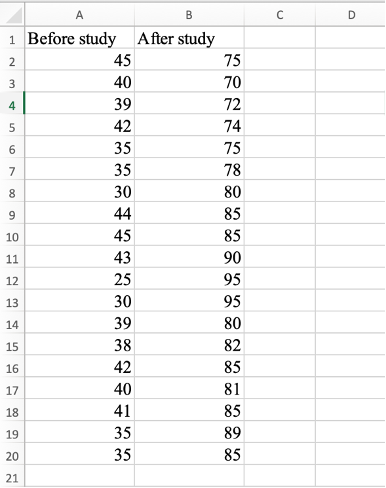
การทดสอบสถิติ paired sample t-test
Step 1: การสร้างชุดข้อมูลใน Excel เพื่อเปรียบเทียบคะแนนสอบก่อนและหลังการศึกษา
ในกรณีนี้มีชุดข้อมูล “Before study” ซึ่งแสดงคะแนนก่อนการศึกษา และอีกชุดหนึ่ง “After study” ซึ่งแสดงคะแนนหลังจากการศึกษา เราจัดเตรียมคะแนนในสองคอลัมน์ โดยคอลัมน์แรกคือคะแนนก่อนการศึกษาและคอลัมน์ที่สองคือคะแนนหลังการศึกษา ข้อมูลนี้สามารถใช้การทดสอบสถิติ “paired sample t-test” ซึ่งเป็นการทดสอบเพื่อดูว่ามีความแตกต่างที่มีนัยสำคัญทางสถิติระหว่างคะแนนก่อนและหลังการศึกษาหรือไม่
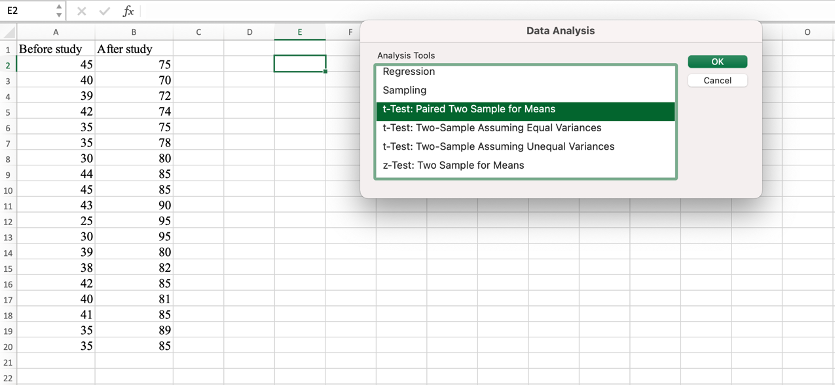
Step 2: สำหรับการทดสอบ paired sample t-test ใน Excel
เราจะเลือก ‘Data Analysis’ จากแถบเมนู ‘Data’.จากนั้นเลือก ‘t-Test: Paired Two Sample for Means’ จากหน้าต่าง ‘Data Analysis’.เราจะต้องระบุช่วงข้อมูลสำหรับคะแนนก่อนการศึกษาและหลังการศึกษาในหน้าต่างที่ปรากฏ หลังจากนั้นคลิก OK เพื่อทำการคำนวณ
Step 3: เลือกหน้าต่าง t-Test: Paired Two Sample for Means
ในหน้าต่าง ‘t-Test: Paired Two Sample for Means’ ให้เลือกช่วงของเซลล์ที่มีข้อมูลคะแนนก่อนและหลังการศึกษาที่เราต้องการนำไปใช้สูตร t-test แบบคู่ (paired sample t-Test) ไม่ต้องระบุค่าเฉลี่ยที่ตั้งสมมติฐานไว้ (Hypothesized Mean Difference) จากนั้นเลือก ‘Labels’ และคลิก OK.
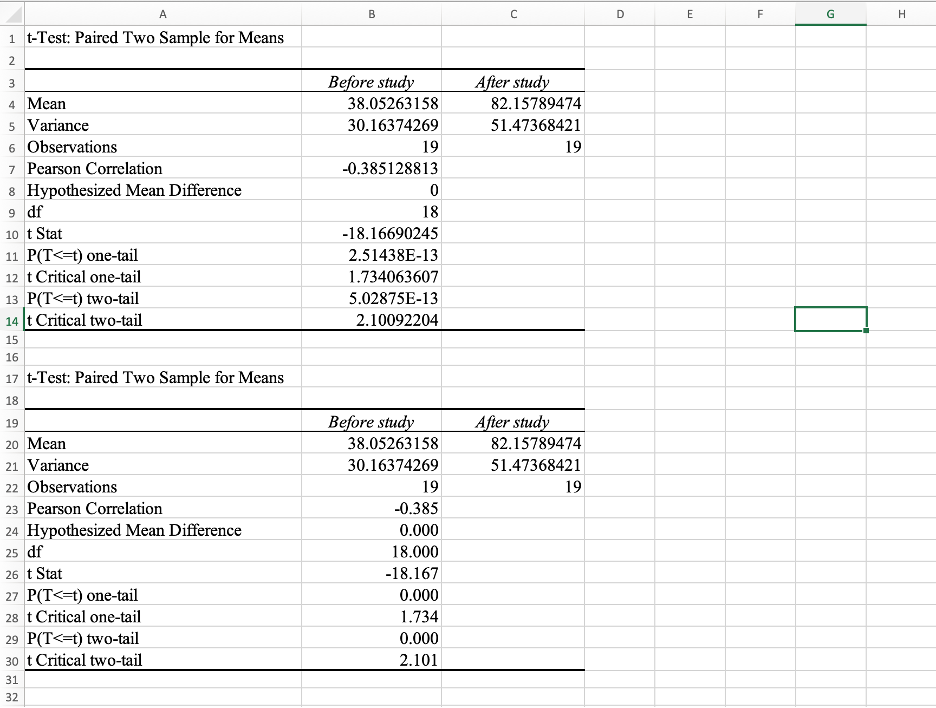
Step 4: การแปลผลการเปรียบเทียบคะแนนสอบก่อนและหลังการศึกษา
การแปลผลการเปรียบเทียบคะแนนสอบก่อนและหลังการศึกษา โดยมีการลดทศนิยมของค่า p ในการทดสอบ ผลลัพธ์แสดงให้เห็นว่าค่า p เท่ากับ 0.000 ซึ่งน้อยกว่า 0.05 ซึ่งแสดงว่าผลการทดสอบนี้ปฏิเสธสมมติฐานหลัก นั่นหมายความว่ามีความแตกต่างอย่างมีนัยสำคัญทางสถิติในคะแนนการสอบก่อนและหลังการศึกษา
สมมติฐานที่ตั้งไว้:
สมมติฐานหลัก (Null Hypothesis, H0): ไม่มีความแตกต่างอย่างมีนัยสำคัญในคะแนนการสอบก่อนและหลังการศึกษา
สมมติฐานทางเลือก (Alternative Hypothesis, H1): มีความแตกต่างที่มีนัยสำคัญในคะแนนการสอบก่อนและหลังการศึกษา
จึงกล่าวสรุปว่าผลลัพธ์จากการทดสอบสถิติ (P-value) น้อยกว่า 0.05, ซึ่งแสดงถึงการปฏิเสธสมมติฐานหลัก (H0) และยอมรับสมมติฐานทางเลือก (H1) ว่า “มีความแตกต่างอย่างมีนัยสำคัญในคะแนนการสอบก่อนและหลังการศึกษา”
หวังว่าบทความ t-test จะเป็นประโยชน์และช่วยให้คุณเข้าใจมากขึ้น ขอให้คุณมีความสุขในการเรียนรู้สถิติและการวิเคราะห์ข้อมูลต่อไปนะคะ ขอบคุณค่ะ

